[Machine Learning] 极大似然估计（Maximum Likelihood Estimate）

极大似然估计

直观想法（举个例子）

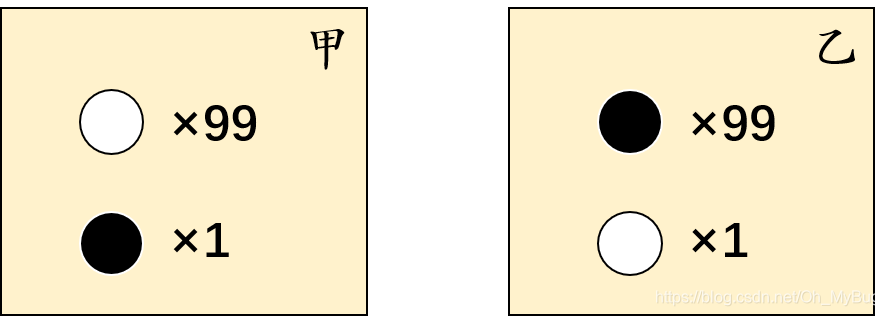
经典例题：有两个外形完全相同地箱子，甲箱中有99只白球，1只黑球；乙箱中有99只黑球，1只白球。一次试验取出一球，结果取出的是黑球。

问：黑球从哪个箱子中取出？

人们的第一印象就是：“此黑球最像是从乙箱中取出”，这个推断符合人们的经验事实。“最像”就是“最大似然”之意，这种想法常称为“最大似然原理”（maximum-likelihood）。

定义

极大似然估计说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次实验，观察其结果，利用结果推出参数地大概值。

极大似然估计是建立在这样的思想上：

已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

离散型

若总体$X$为离散型，其概率分布列为

P { X = x } = p ( x ; θ ) P\{X=x\}=p(x;\theta) P{ X=x}=p(x;θ)

其中$\theta$为未知参数。设$(X_1,X_2,...,X_n)$是取自总体的样本容量为$n$的样本，则$(X_1,X_2,...,X_n)$的联合分布律为${\Pi }_{i=1}^{n}p(x_i;\theta )$。

又设$(X_1,X_2,...,X_n)$有一组观测值为$(x_1,x_2,...,x_n)$，易知样本$(X_1,X_2,...,X_n)$取到观测值$(x_1,x_2,...,x_n)$的概率为

$$L(\theta )=L(x_1,x_2,...,x_n;\theta )={\Pi }_{i=1}^{n}p(x_i;\theta )$$

这一概率随$\theta$的取值而变化，它是$\theta$的函数，称$L(\theta )$为样本的似然函数。

连续型

若总体$X$为连续型，其概率密度函数为

$$f(x;\theta )$$

其中$\theta$为未知参数。设$(X_1,X_2,...,X_n)$是取自总体的样本容量为$n$的样本，则 ( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n)