洛谷 P2341 [HAOI2006]受欢迎的牛

题目描述

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 $A$ 喜欢 $B$，$B$ 喜欢 $C$，那么 $A$ 也喜欢 $C$ 。牛栏里共有 $N$ 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

输入输出格式

输入格式：

第一行：两个用空格分开的整数：$N$ 和 $M$
第二行到第 $M+1$ 行：每行两个用空格分开的整数：$A$ 和 $B$，表示 $A$ 喜欢 $B$

输出格式：

第一行：单独一个整数，表示明星奶牛的数量

输入输出样例

输入样例#1：

3 3
1 2
2 1
2 3

输出样例#1：

1

说明

只有 $3$ 号奶牛可以做明星

数据范围

$10\%$ 的数据$N\leq 20, M\leq 50$

$30\%$ 的数据$N\leq 1000, M\leq 20000$

$70\%$ 的数据$N\leq 5000, M\leq 50000$

$100\%$ 的数据$N\leq 10000, M\leq 50000$

---

solution

• 一道比较裸的缩点

• 先跑一遍Tarjan求出强连通分量，然后缩点，统计每个点的出度

• 如果只有一个点的出度为 $0$ ，那图大概是这样的

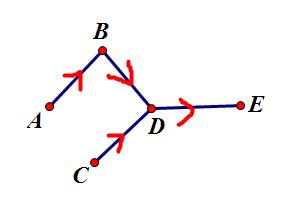
• 这样 $E$ 这个点的奶牛就被所有的奶牛喜欢啦，所以他们他们都是明星，直接输出 $E$ 这个点包含多少奶牛

• 如果不止一个点的出度为 $0$，那图大概是这样的

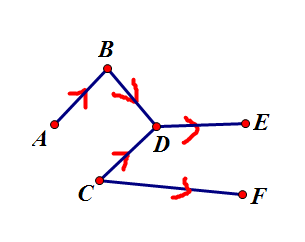
• 这样没有奶牛被所有的奶牛喜欢，应该直接输出

code

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;

template<typename ____>
void _____(____ &___) {//听说这么写读入优化会增加代码有bug的几率qwq
    ___=0; ____ __=1;
    register char _=getchar();
    for(;_<'0'||_>'9';_=getchar())
        if(_=='-') __=-1;
    for(;_>='0'&&_<='9';_=getchar())
        ___=___*10+_-'0';
    ___*=__;
    return;
}

#define MAXN 10010
#define MAXM 50010

struct Edge {
    int u,v,next;
    Edge(int u=0,int v=0,int next=0):
        u(u),v(v),next(next) {}
};

Edge edge[MAXM];
int head[MAXN],cnt;

void addedge(int u,int v) {
    edge[++cnt]=Edge(u,v,head[u]);
    head[u]=cnt;
    return;
}

int dfn[MAXN],low[MAXN],timee;
int st[MAXN],top;
int col[MAXN],numcolor;
bool vis[MAXN],ins[MAXN];
int num[MAXN];

void dfs(int now) {
    dfn[now]=low[now]=++timee;
    st[++top]=now;
    vis[now]=ins[now]=true;
    for(int i=head[now];i;i=edge[i].next) {
        int v=edge[i].v;
        if(ins[v]) low[now]=min(low[now],dfn[v]);
        else if(!vis[v]) {
            dfs(v);
            low[now]=min(low[now],low[v]);
        }
    }
    if(dfn[now]==low[now]) {
        col[now]=++numcolor;
        num[numcolor]++;
        while(st[top]!=now) {
            col[st[top]]=numcolor;
            num[numcolor]++;
            ins[st[top--]]=false;
        }
        ins[now]=false;
        top--;
    }
    return;
}


int outdeg[MAXN];

int main() {
    int n,m;
    _____(n),_____(m);
    for(int i=1,A,B;i<=m;i++) {
        _____(A),_____(B);
        addedge(A,B);
    }
    for(int i=1;i<=n;i++)
        if(!vis[i]) dfs(i);
    for(int u=1;u<=n;u++)
        for(int i=head[u];i;i=edge[i].next)
            if(col[u]!=col[edge[i].v])
                outdeg[col[u]]++;
    int sum=0,color;
    for(int i=1;i<=numcolor;i++)
        if(outdeg[i]==0) sum++,color=i;
    if(sum==1) printf("%d\n",num[color]);
    else printf("0");
    return 0;
}