本文详细解释了卷积神经网络中如何通过计算确定相同填充大小，特别是在步长为1且无膨胀时的特殊情况，并强调了相同填充在步长和膨胀系数变化下的输出尺寸调整。同时提到深度学习框架如PyTorch中的自动处理机制。
在卷积神经网络中，要使得卷积层的输出维度（特别是空间维度，即宽度 W 和高度 H）与输入维度相同，需要使用所谓的“相同”（same）填充。"相同"填充的计算方式取决于卷积核的尺寸（kernel size）、步长（stride）和膨胀系数（dilation）。以下是如何确定相同填充大小的通用方法：
相同填充大小的计算
假设：
- 卷积核尺寸为
k（对于不同的高度和宽度，可以是kh和kw）。 - 步长为
s（对于不同的高度和宽度，可以是sh和sw）。 - 膨胀系数为
d（对于不同的高度和宽度，可以是dh和dw）。
填充大小 p 可以通过以下公式计算：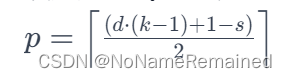
其中 ⌈x⌉ 表示对 x 向上取整。
特殊情况
-
当步长为 1（
s = 1）且没有膨胀（d = 1）时，公式简化为：k-1/2 这是最常见的情况，例如，3x3 的卷积核将需要 1 的填充（p = 1）。 -
对于步长大于 1 的情况，输出维度将小于输入维度，即使使用相同填充。在这种情况下，相同填充只能确保输出大小接近输入大小的一个整数倍。
注意事项
- 相同填充保证了卷积操作后输出的空间维度与输入相同，但这只在步长为 1 时完全成立。
- 当步长大于 1 或膨胀系数不为 1 时，输出的空间维度可能会与输入有所不同，但相同填充仍然有助于控制输出大小。
在实际应用中，许多深度学习框架提供了选项来自动计算并应用相同填充，简化了这一过程。例如，PyTorch 中的 nn.Conv2d 在设置 padding='same' 时会自动计算并应用适当的填充。
扫一扫
773
到【灌水乐园】发言
