卷积的数学理解和图像处理

一种通俗的方法理解卷积，上面的图是一天的进食量（无时无刻不断进食），下面是食物随着时间的消化比例，求某一个时刻胃内还剩多少食物？

在某个t时刻实际上是这样对应计算的，然后把所有的计算值加起来。

 

当一个系统输入不稳定，输出稳定，就可以用卷积来求系统存量。

换一个通俗的例子，在t时刻发生了飓风，原因是在之前有很多蝴蝶扇动了翅膀，会对发生飓风产生影响，这个影响力是会随着时间的变化而变化的，这个变化函数就是g函数。卷积操作就是看在飓风发生的时候之前蝴蝶扇动的翅膀对自己产生了多少影响。

总结就是，在某一个时刻发生了一件事，而这件事情的发生是受到之前发生的很多事情的影响，g函数就是发生的事情随着时间是如何变化的，横坐标也可以改成距离等等

 那么什么是图像的卷积操作？

图像是函数f，卷积核是函数g。就是看很多像素点对某一个像素点是如何产生影响的。

卷积核就是规定了周围的像素点是如何对当前的像素点产生影响的。

比如平滑卷积操作：

 就是让周围的像素点和自己相差不要太大，其实就是求平均值，所以可以让图像变得平滑。

至于周围的多大范围像素点可以对当前像素点产生影响？那就要看卷积核的大小了。

图像卷积进行逆向的数学解释：

 可以看到实际上不是按照相应的位置进行乘积的，可以将卷积核旋转一下

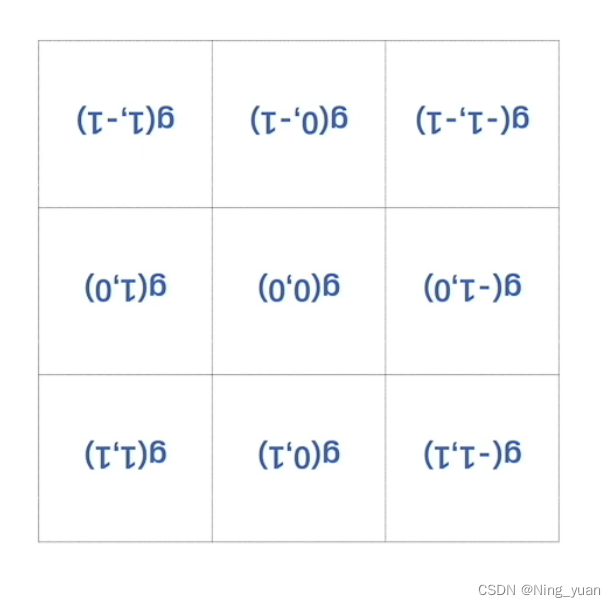
 因此可以知道g函数不等于卷积核，卷积核是g函数的旋转

再来看看例子：

 这两个卷积核该怎么理解呢？

他们是分别把图像的纵向和横向的边界特征挑选了出来，咦？好像不是周围像素点对当前像素点的影响了？ 

如果卷积核挑选的合适，可以对图片进行过滤，把某些特征保存下来，其他特征过滤掉，这样的卷积核也叫过滤器。

可以看作自己对周围像素点的试探，卷积核就是试探模板，当你不像考虑某个位置的时候设置成0，重点考虑就设置的值比较大，通过卷积核把周围有用的特征保留下来。

当图像完美匹配卷积核想要提取的特征时：

这种不是完美匹配，但也能提取出来里面有部分相同特征：

 

卷积操作得到与这个特征匹配的全部信息：

 

三个特征都进行卷积：