零基础-动手学深度学习-4.8. 数值稳定性和模型初始化

鄙人生医转码，道行浅薄请见谅~仅作笔记交流使用

初始化方案的选择在神经网络学习中起着举足轻重的作用， 它对保持数值稳定性至关重要，糟糕选择可能会导致我们在训练时遇到梯度爆炸或梯度消失：

一、梯度消失和梯度爆炸

考虑一个具有L层、输入x和输出o的深层网络。 每一层l由变换fl定义， 该变换的参数为权重W(l)， 其隐藏变量是h(l)（令 h(0)=x），其中fL是损失函数，我们的网络可以表示为：

如果所有隐藏变量和输入都是向量， 我们可以将o关于任何一组参数W(l)的梯度写为下式：

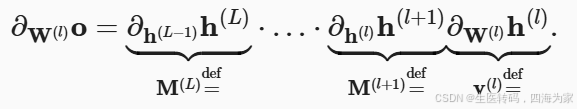
这个式子书上看感觉有点点奇怪，我copy一下视频上面的式子一目了然：

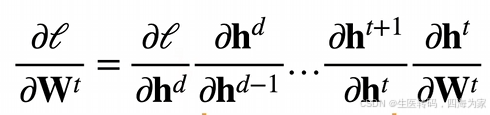
其中会有目标层和现有层的差次的矩阵乘法，换言之，该梯度是L−l个矩阵 M(L)⋅…⋅M(l+1) 与梯度向量 v(l)的乘积， 因此，我们容易受到数值下溢问题的影响. 当将太多的概率乘在一起时，这些问题经常会出现

不稳定梯度带来的风险不止在于数值表示； 不稳定梯度也威胁到我们优化算法的稳定性。 我们可能面临一些问题。 要么是梯度爆炸问题： 参数更新过大，破坏了模型的稳定收敛； 要么是梯