目录
仅当笔记本使用,鄙人为零基础转码博主,道行浅薄,请见谅~
一、线性回归的基本元素
1.假设:自变量x与因变量y存在线性关系
2.样本:数据点或者数据样本
3.特征:预测所依据的协变量
4.目标:标签或者目标
二、线性模型
![]()
其实也就是初高中的回归模型演化,当然一个公式可能看起来并不是非常的明确,我没有写每个字母的具体含义,通常再机器学习中使用的都是高维数据集,因此wx实际上已经不是普通回归模型的简单乘法而是矩阵乘法的算法:
![]()
意义就是向量x1,x2,实际上都是由多个特征组成的特征,这么说有点绕口,用最简单的例子来说,就是一个房子的价格取决于一个房子的大小,年龄,坐标等,然后去构建一个线性模型预测时需要考虑所有这些特征并乘以其权重(可能房子的大小会比其年龄更加重要?),然后得到一个输出也就是我们的目标值,这些值可以分开写,也可以直接用一个矩阵搞定。
三、损失函数
损失函数这个东西就是预测值与实际值(来源于训练集)的偏差,衡量这个值有很多数学方法和定式,但是我们这里先用最熟悉的平方差:
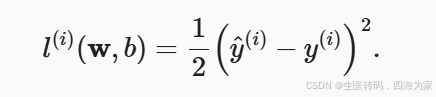
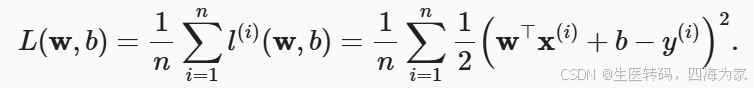
下面的公式就是把刚刚写的模型带入,我们要做的事情就明了了,寻找一组w(权重),b(偏差),使得我们的损失最小。
四、解析解
解析解这里比较有趣,如果学习了吴恩达老师的机器学习我们可以进行这样的想象,在有非常多“山谷”的凹函数空间中,会有非常多的局部最优值,很难直接从数学上去解这样的最值,但是在线性回归问题中,这个凸函数由于太过简单,就只有一个局部最优值,因此我们讲能得到其一个最优解,就像我们高中得到的线性回归最佳ab值一样,我们可以写一个解析解出来:
![]()
一开始我看到这个解析解是比较蒙的,因为作为生医废材我的线性代数实在时看不下去,所以我就进行了一点资料的查阅得出了这个结果,因为博主懒得写公式,我这里就简单写一下思想过程,首先展开损失函数为矩阵和矩阵转置相乘,然后对w求导,这里要先把展开的矩阵拆开,运用到二次型矩阵和常数矩阵与向量的求导法则,能得到一个比较简洁的形式,然后同时乘以(xtx)-1就可以了。
五、随机梯度下降
随机梯度下降几乎可以说是在计算机上实现线性回归最核心的思想,这部分建议还是看看吴恩达老师的机器学习,但你可以进行想象,我们在去到达一个最低的loss值就是去寻找一群山的最低的山谷,当我们以目前眼前能看到,腿能迈出最大一步的方向,肯定要是最垂直下落的方式是最快的,因此我们运用高数中的梯度求解,以一定的步距朝着每次到达点的最垂直的方向走,肯定是以比较快的方式到达山谷,而且大概率不会瞎跑。
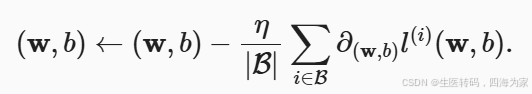
六、从线性回归到深度网络
为什么要学习线性回归,这和深度学习有什么关系?我觉得就用下面一张图来解释:
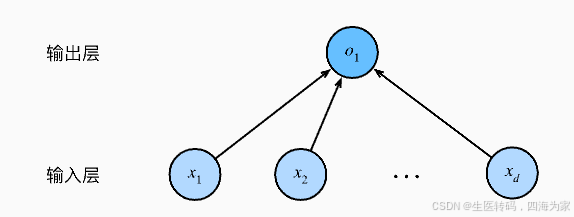
没错,线性回归就是一个单层的深度学习神经网络





















 874
874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








