机器学习经典算法：简单线性回归（一元）

正文

一元线性回归是一种基本的回归分析方法，用于研究一个自变量与因变量之间的线性关系。它通过拟合一条直线来预测因变量的值，模型可以估计出最佳的截距和斜率，从而实现对新数据的预测。一元线性回归广泛应用于经济学、统计学、工程等领域，用于建立简单的预测模型。

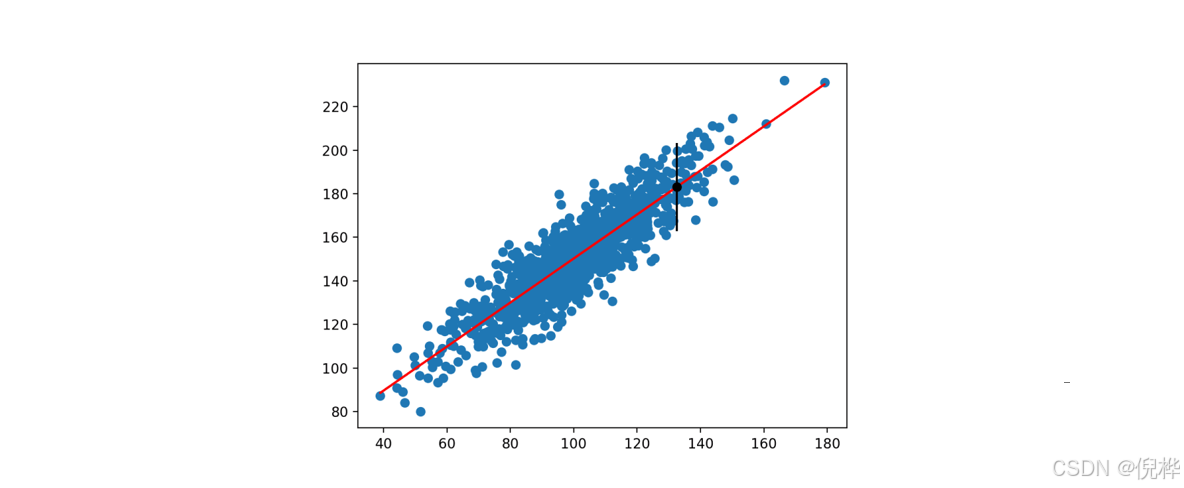
特点：主要用于解决回归问题，线性回归是许多强大非线性模型的基础(多项式回归，逻辑回归，SVM，神经网络…本质都是线性回归的拓展，寻找最优参数)，其结果具有很好的可解释性。
 \,
假设样本特征与样本输出标记之间存在线性关系，那么就可以寻找一条直线来最大程度拟合它们之间的关系。
 \,
① 简单线性回归： 样本特征只有一个的回归拟合($ y = ax+ b$);
② 多元线性回归： 多样本特征与样本输出标记之间的回归拟合。

1、简单线性回归简介

假设样本特征与样本输出标记之间存在线性关系，这个线性关系由最佳拟合的直线方程$y=ax+b$所表示，则对于每个样本点$x^{(i)}$，就有预测值${\hat{y}}^{(i)}=a{x}^{(i)}+b$,其真值为$y^{(i)}$。样本点 ${\hat{y}}^{(i)}$ 与 $y^{(i)}$ 的 差距 可由 $|{\hat{y}}^{(i)}-$