对于 Au⃗=λu⃗A\vec u = \lambda \vec uAu=λu,对应一个特征值λ\lambdaλ 的特征向量不唯一;求解特征向量的过程在于求解齐次线性系统(A−λI)u⃗=O(A - \lambda I)\vec u = O(A−λI)u=O,并且由于u⃗!=O\vec u != Ou!=O,所以该线性系统存在一组解[u⃗1,u⃗2...][\vec u_1,\vec u_2...][u1,u2...],也即特征向量组成了 A−λIA - \lambda IA−λI的零空间(刨除零向量)。
对应特征值λ\lambdaλ 的特征向量的解空间又称 λ\lambdaλ 的特征空间( EλE_{\lambda}Eλ ) : Eλ={O}∪{λ的特征向量}\, \, E_{\lambda} = \{O\} \cup \{\lambda \small 的特征向量\}Eλ={O}∪{λ的特征向量}。
对于一个nnn阶变换矩阵AAA,则其对应求解特征向量的行列式det(A−λI)=O\det (A - \lambda I) = Odet(A−λI)=O展开后得到的将是一个关于λ\lambdaλ的 nnn 次方程(在实数域和复数域内,λ\lambdaλ对应nnn个解)。
关于特征值的解的3种情况:
① λ\lambdaλ在实数域内存在nnn个互不相等的解,n1 !=n2 !=... !=nnn_1 \ \ != n_2 \ \ != ... \ \ != n_nn1 !=n2 !=... !=nn,这些特征值称为简单特征值(应用最多);
② λ\lambdaλ在实数域内存在的nnn个解中包含重复值,ni=nj=...=nkn_i = n_j =... = n_kni=nj=...=nk,则称这些重复的特征值为多重特征值,使用重数\color {red} {\small 重数}重数来描述重复特征值的重复次数;
③ λ\lambdaλ在实数域内无解,仅在复数域有解,如det(A−λI)=λ2+1=0→λ1=i;λ2=−i\det (A - \lambda I) = \lambda ^2 + 1 = 0 \rightarrow \lambda_1 = i ; \lambda_2 = -idet(A−λI)=λ2+1=0→λ1=i;λ2=−i ,这种情况称为复数特征值。
如果存在λ=0\lambda = 0λ=0是矩阵AAA的一个特征值,意味着对于线性方程Au⃗=λu⃗→Au⃗=OA\vec u = \lambda \vec u \rightarrow A\vec u = OAu=λu→Au=O,要使得u⃗≠O\vec u \neq Ou=O,则矩阵AAA一定不可逆,所以当矩阵AAA可逆就有λ≠0\lambda \neq 0λ=0。
#####关于一些特殊矩阵的特征方程求解:
① 对角矩阵
A= [d10...00d2...000...dn]→ det(A)=d1∗d2∗...∗dnA =\ \ \ \ \ \ \begin {bmatrix} d_1&0&...&0 \\ 0&d_2&...&0 \\ 0&0&...&d_n \\ \end {bmatrix} \rightarrow \ \ \ \ \ \ \ \ \ \ \ \ \det(A) = d_1*d_2*...*d_nA= d1000d20.........00dn→ det(A)=d1∗d2∗...∗dn
A−λI=[d1−λ0...00d2−λ...000...dn−λ]→det(A−λI)=(d1−λ)∗(d2−λ)∗...∗(dn−λ)A-\lambda I = \begin {bmatrix} d_1 - \lambda&0&...&0 \\ 0&d_2 - \lambda&...&0 \\ 0&0&...&d_n - \lambda \\ \end {bmatrix} \rightarrow \det(A-\lambda I) = (d_1 - \lambda)*(d_2 - \lambda)*...*(d_n - \lambda)A−λI=d1−λ000d2−λ0.........00dn−λ→det(A−λI)=(d1−λ)∗(d2−λ)∗...∗(dn−λ)
∴λ1=d1;λ2=d2;...λn=dn\therefore \lambda_1 = d_1;\lambda_2 = d_2;...\lambda_n = d_n∴λ1=d1;λ2=d2;...λn=dn
同理可直接求取上三角,下三角形状的变换矩阵AAA的特征值。
关于特征值的一些基本性质:
-
若λ\lambdaλ是AAA的特征值,则有λm\lambda ^mλm是AmA ^mAm的特征值(m≥1)(m \ge 1)(m≥1);
\, \, \, \, \, 数学归纳 ∵m=1\because m =1∵m=1 成立,Au⃗=λu⃗A\vec u = \lambda \vec uAu=λu
\, \, \, \, \, \, \, \, \, \, \, \, \, 假设 m=kAku⃗=λku⃗\, \, m =k A ^ k \vec u = \lambda ^ k \vec um=kAku=λku
\, \, \, \, \, \, \, \, \, \, \, \, \, 当 m=k+1\, \, \, \, \, m =k+1m=k+1 时,Ak+1u⃗=A∗Aku⃗=Au⃗∗λk=λu⃗∗λk=λk+1u⃗A ^ {k+1} \vec u = A * A^k \vec u = A \vec u* \lambda ^ k = \lambda \vec u * \lambda ^ k = \lambda ^ {k+1} \vec {u}Ak+1u=A∗Aku=Au∗λk=λu∗λk=λk+1u 得证假设。 -
若λ\lambdaλ是 AAA 的特征值,则有 λ−1\lambda ^{-1}λ−1 是 A−1A ^{-1}A−1 的特征值(已给出前提矩阵AAA可逆);
\, \, \, \, \, 由 Au⃗=λu⃗\, \, A\vec u = \lambda \vec uAu=λu
A−1∗Au⃗=A−1∗λu⃗\, \, \, \, \, \, \, \, \, \, \, A^{-1}* A\vec u = A^{-1}* \lambda \vec uA−1∗Au=A−1∗λu
u⃗=λ∗A−1u⃗→u⃗λ−1=A−1u⃗\, \, \, \, \, \, \, \, \, \, \, \, \vec u = \lambda*A^{-1}\vec u \rightarrow \vec u \lambda ^{-1} = A^{-1}\vec uu=λ∗A−1u→uλ−1=A−1u得证。
在线性代数上的理解:
通过特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个子空间,我们可以利用这些线性的子空间干很多的事情。
线性变换矩阵的特征值和特征空间–几何理解
- 投影变换
在二维空间,把任意向量都投影到u⃗=(2,1)\vec u = (2,1)u=(2,1)所在直线的变换中,变换前后方向保持不变的向量Aa⃗=a⃗′=λa⃗A\vec a = \vec a{'}= \lambda \vec aAa=a′=λa将存在于直线y=0.5xy = 0.5xy=0.5x上,且这些向量经投影变换后大小不变即λ=1\lambda = 1λ=1,所以该直线上的所有向量构成了投影矩阵AAA中λ=1\lambda =1λ=1的解空间。除了直线上的向量,垂直于直线的向量投影到直线上将变成零向量OOO,而OOO与变换前的向量同向,不过长度为零,所以垂直于y=0.5xy = 0.5xy=0.5x的直线上的所有向量构成了投影矩阵AAA中λ=0\lambda =0λ=0的解空间。
- 对称变换
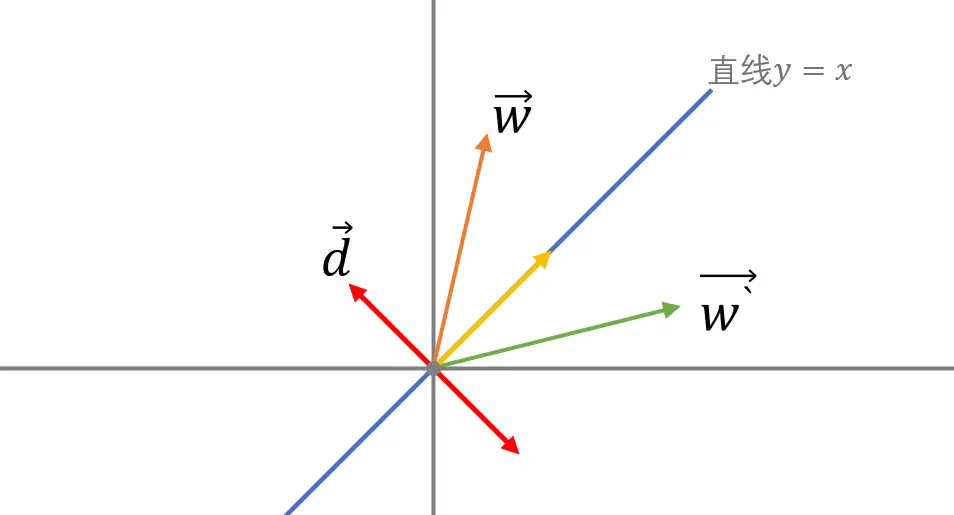
在二位空间中,变化矩阵A=[0110]A= \begin {bmatrix} 0&1 \\ 1&0 \end {bmatrix}A=[0110]将平面上的所有向量关于直线 y=xy = xy=x 对称变换。那么对处于y=xy = xy=x直线上的任意向量,对称前后将等大同向,所以这些向量构成了 AAA中λ=1\lambda =1λ=1 的解空间。而对于垂直于 y=xy = xy=x 的直线 y=−xy = -xy=−x 上的向量,这些向量对称前后将等大反向,因此构成了 AAA中λ=−1\lambda =-1λ=−1的解空间。
旋转矩阵的特征值和特征空间–几何理解
对于空间中任意一个向量u⃗\vec uu经过旋转变换得到的向量v⃗\vec vv,几何中不会存在任何v⃗\vec vv与向量u⃗\vec uu同向。所以,对于旋转矩阵AAA,如逆时针90°旋转矩阵A=[0−110]A= \begin {bmatrix} 0&-1 \\ 1&0 \end {bmatrix}A=[01−10],求解其特征值将得到det(A−λI)=O→λ2+1=0\det(A - \lambda I) = O \rightarrow \lambda ^2 + 1 = 0det(A−λI)=O→λ2+1=0,意味着其特征值只能在复数空间寻求解。

























 1821
1821

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










