线性代数：找到二维空间的一组正交基（一维投影）

正文

在实际情况中，对于一个空间，我们通常只能获取到这个空间的随意一组基，这样的一组基内的向量大概率不是正交关系的，我们得到的空间的基与矩阵的形状密切相关。但是，对于给定的一个空间的一组基，我们可以进一步的找到这个空间的一组正交基，一个空间的标准正交基方便计算。

获取空间的一组标准正交基的步骤

首先，获取空间的一组基
继而求取空间的正交基
最后获取空间的标准正交基 $u^\hat u$ ， $u^=1∥u⃗∥⋅u⃗=(u1∥u⃗∥,u2∥u⃗∥,⋯ ,un∥u⃗∥)\hat u = \frac {1}{\| \vec u\|} \cdot \vec u = (\frac {u_1}{\| \vec u\|},\frac {u_2}{\| \vec u\|},\cdots , \frac {u_n}{\| \vec u\|})$

从上面整个步骤可以看出，求取一个空间的标准正交基，关键是求取空间的正交基。

求取一个二维平面的一组正交基

在一个二维空间，给出空间的任意一组基 $v⃗\vec u , \ \vec v$ ，首先这两个向量一定不共线，那么在二维平面这两向量可以表示成

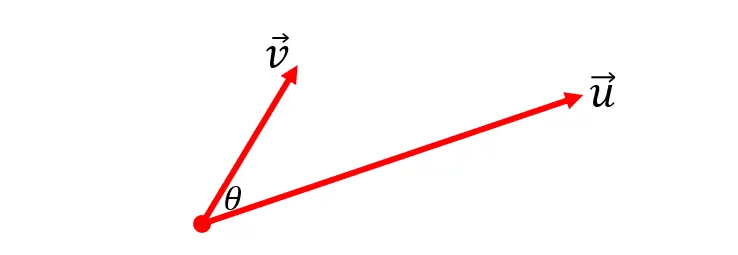
然后通过这组向量来求取二维平面的正交基，只需让这组向量的其中一个向量保持不变，令另一个向量与保持不变的这向量垂直，这样就得到了二维平面的一组正交基。这里假设让这个二维平面的基中的向量 $u⃗\vec u$ 保持不变。
接下来需要找到一个与向量 $u⃗\vec u$ 垂直的向量：具体操作为
① 从向量 $v⃗\vec v$ 向 $u⃗\vec u$ 作投影，即向量 $v⃗\vec v$ 所在的线段的末端向向量 $u⃗\vec u$ 所在的线代作垂线，那以垂足的位置作为另外一个向量 $p⃗1\vec p_1$ 的末端，那么这个向量 $p⃗1\vec p_1$ 就是向量 $v⃗\vec v$ 在向量 $u⃗\vec u$ 的投影。

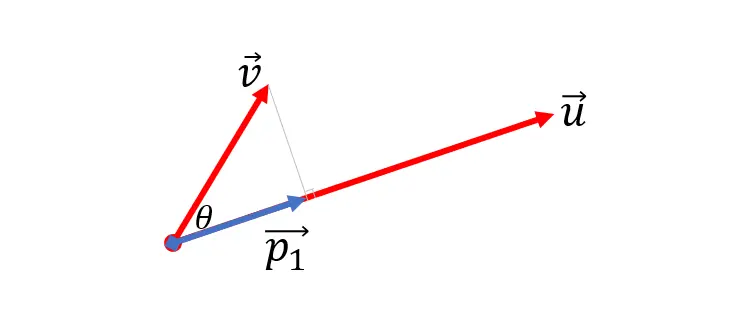
②通过向量 $p⃗1\vec p_1$ ，进一步就可以通过向量减法，求出与向量 $u⃗\vec u$ 垂直的那个向量 $p⃗2\vec p_2$ ,按照向量的平行四边形法则，向量 $p⃗2\vec p_2$ 加上 $p⃗1\vec p_1$ 向量得到 $v⃗\vec v$ 向量，所以 $p⃗2=v⃗−p⃗1\vec p_2= \vec v - \vec p_1$ ：

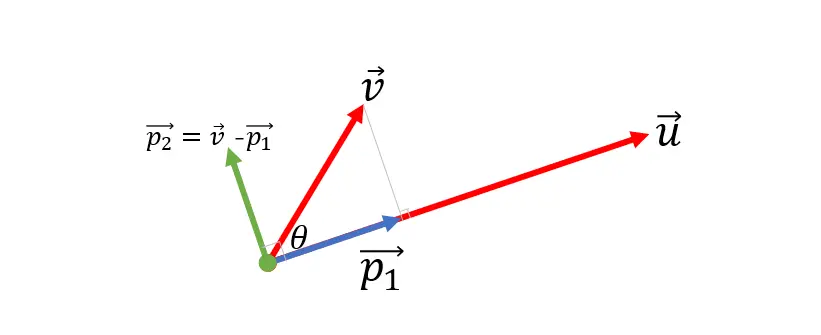
至此，就在在一个二维空间找到的两个向量 $p⃗2\vec p_2$ 和向量 $u⃗\vec u$ ，它们就是这个二维空间的一组正交基。在这个过程中，核心就是求出向量 $v⃗\vec v$ 在 $u⃗\vec u$ 的投影向量 $p⃗1\vec p_1$ 。

求出投影向量 $p⃗1\vec p_1$
对于向量的点乘 $u⃗⋅v⃗=∥u⃗∥⋅∥v⃗∥⋅cos⁡θ\vec u \cdot \vec v = \| \vec u \| \cdot \| \vec v \| \cdot \cos \theta$
根据三角函数的知识，就有向量的 $p⃗1\vec p_1$ 的模 $∥p⃗1∥=∥v⃗∥⋅cos⁡θ=u⃗⋅v⃗∥u⃗∥\| \vec p_1 \| = \| \vec v \| \cdot \cos \theta = \frac {\vec u \cdot \vec v}{\| \vec u \|}$
由于向量 $p⃗1\vec p_1$ 与向量 $u⃗\vec u$ 共线，所以向量 $p⃗1\vec p_1$ 的方向等于向量 $u⃗\vec u$ 的方向,向量 $u⃗\vec u$ 的方向就是它的标准单位方向向量，即 $u⃗∥u⃗∥\frac {\vec u}{\| \vec u\|}$
最后，由向量 $p⃗1\vec p_1$ 的标准单位方向向量和向量 $p⃗1\vec p_1$ 的模相乘就可以完整表示向量 $p⃗1=∥p⃗1∥⋅u⃗∥u⃗∥=u⃗⋅v⃗∥u⃗∥⋅u⃗∥u⃗∥=u⃗⋅v⃗∥u⃗∥2⋅u⃗\vec p_1 = \| \vec p_1 \| \cdot \frac {\vec u}{\| \vec u\|} = \frac {\vec u \cdot \vec v}{\| \vec u \|} \cdot \frac {\vec u}{\| \vec u\|} = \frac {\vec u \cdot \vec v}{\| \vec u \|^2} \cdot {\vec u}$
又 $∵u⃗⋅u⃗=∥u⃗∥2\because \vec u \cdot \vec u = \| \vec u \|^2$
$∴p⃗1=u⃗⋅v⃗u⃗⋅u⃗⋅u⃗\therefore \vec p_1 = \frac {\vec u \cdot \vec v}{\vec u \cdot \vec u} \cdot {\vec u}$ ，注意不能约分，向量点乘与标量数乘是不一样的。
通过向量 $p⃗1\vec p_1$ ，进而就可以计算出与向量 $u⃗\vec u$ 正交的向量 $p⃗2=v⃗−p⃗1\vec p_2 = \vec v - \vec p_1$