从区块链到DAG（三）--DAG共识之SPECTRE协议

承接上一篇结尾提出的问题，接下来的文章会着重介绍DAG的账本共识SPECTRE协议。从上一篇（《从区块链到DAG（二）--DAG的基本结构》）可以看出，DAG的整个网络并不是线性的。SPECTRE协议顺应了这种结构所以并没有提出选择主链的概念，而是着眼于解决冲突交易和防止恶意攻击。这里需要声明一下，所有讨论账本共识有效有个大前提：网络中大多数节点都是诚实的。我们不考虑集中超过51%算力的这种恶意攻击，因为无论用什么账本共识这样的攻击都会奏效。

 

 1.  SPECTRE如何解决冲突交易

SPECTRE通过区块间的投票来排除冲突的交易，如图1。

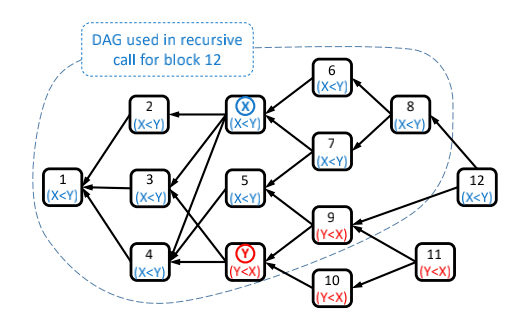
图片1 一个简单的DAG网络的投票过程

来源：Yonatan Sompolinsky, Yoad Lewenberg, and Aviv Zohar，《SPECTRE:Serialization of Proof-of-work Events: Confifirming Transactions viaRecursive Elections》

 

区块X里记录的交易信息是交易x先于交易y发生，记为x<y ；区块Y里记录的交易信息是交易y先于交易x发生，记为y<x，这两个交易相互冲突。

投票过程：

区块X和区块Y分别投票给自己。

区块X之后产生的区块我们称之为X的未来区块，回溯这些未来区块发现6，7，8只能回溯到X，所以这三个区块都投票给X，标记为蓝色。同理，回溯区块Y的未来区块发现9，10，11只能投票给Y，标记为红色。

未来区块12既回溯到X又能回溯到Y，它会投出与上一轮投票一样的结果X。图中虚线部分是上一轮的投票，按少数服从多数的原则可知，投票的结果是X。

X或Y之前产生的区块我们称为X或Y的过去区块，这些区块会分别统计自己对应的未来区块的投票，然后跟投给得票较多的那个选项。由此，区块1～5都投给X，交易x<y认定有效，y<x被丢弃。

 

 2.  “最长链共识”与SPECTRE的关系

图片2展示了当SPECTRE应用在区块链结构上的情况。