Leetcode广度优先搜索笔记3 二进制矩阵中的最短路径

1091. 二进制矩阵中的最短路径：广度优先搜索解决矩阵中的路径寻找问题

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

·路径途经的所有单元格都的值都是 0 。
·路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度 是该路径途经的单元格总数。

示例 1：

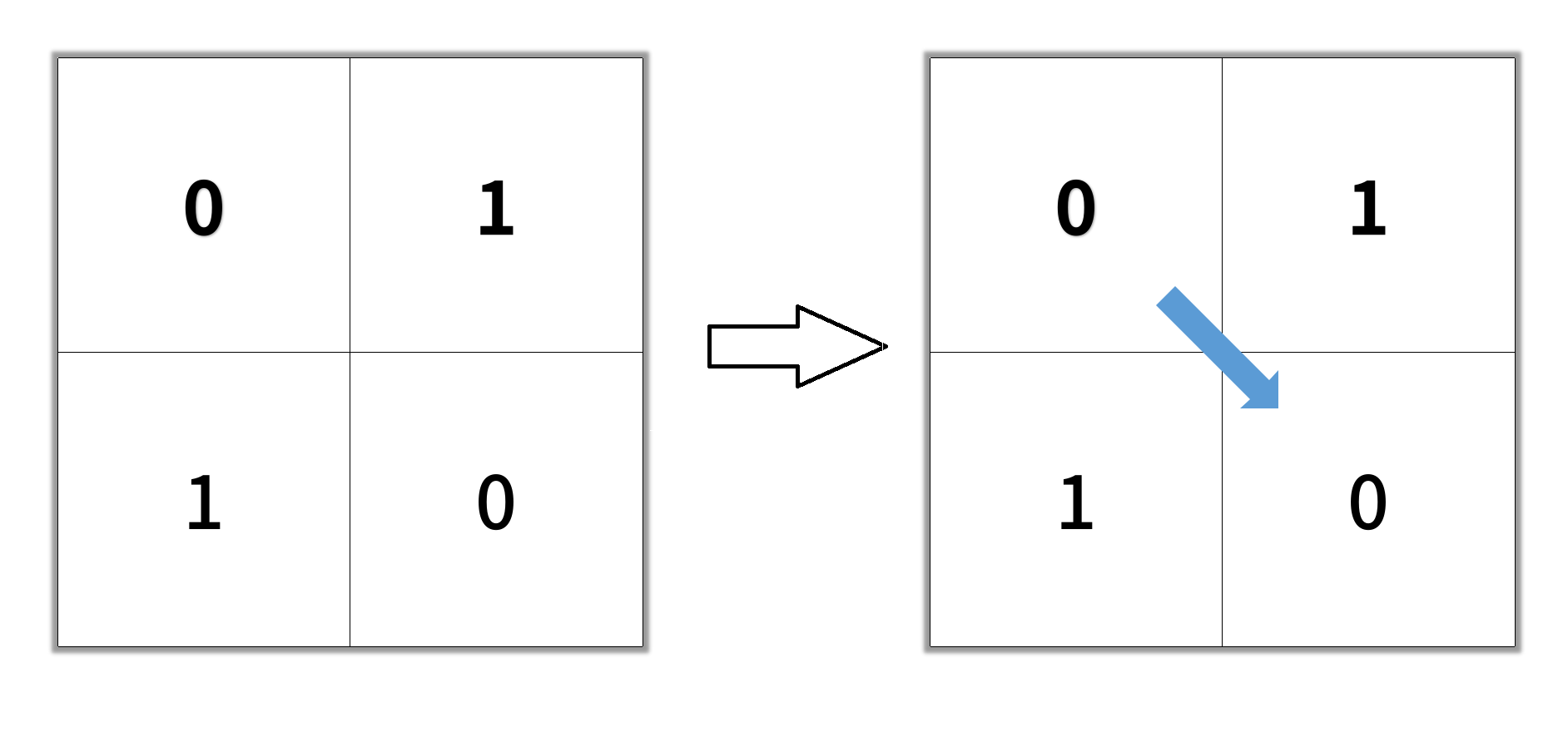
输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

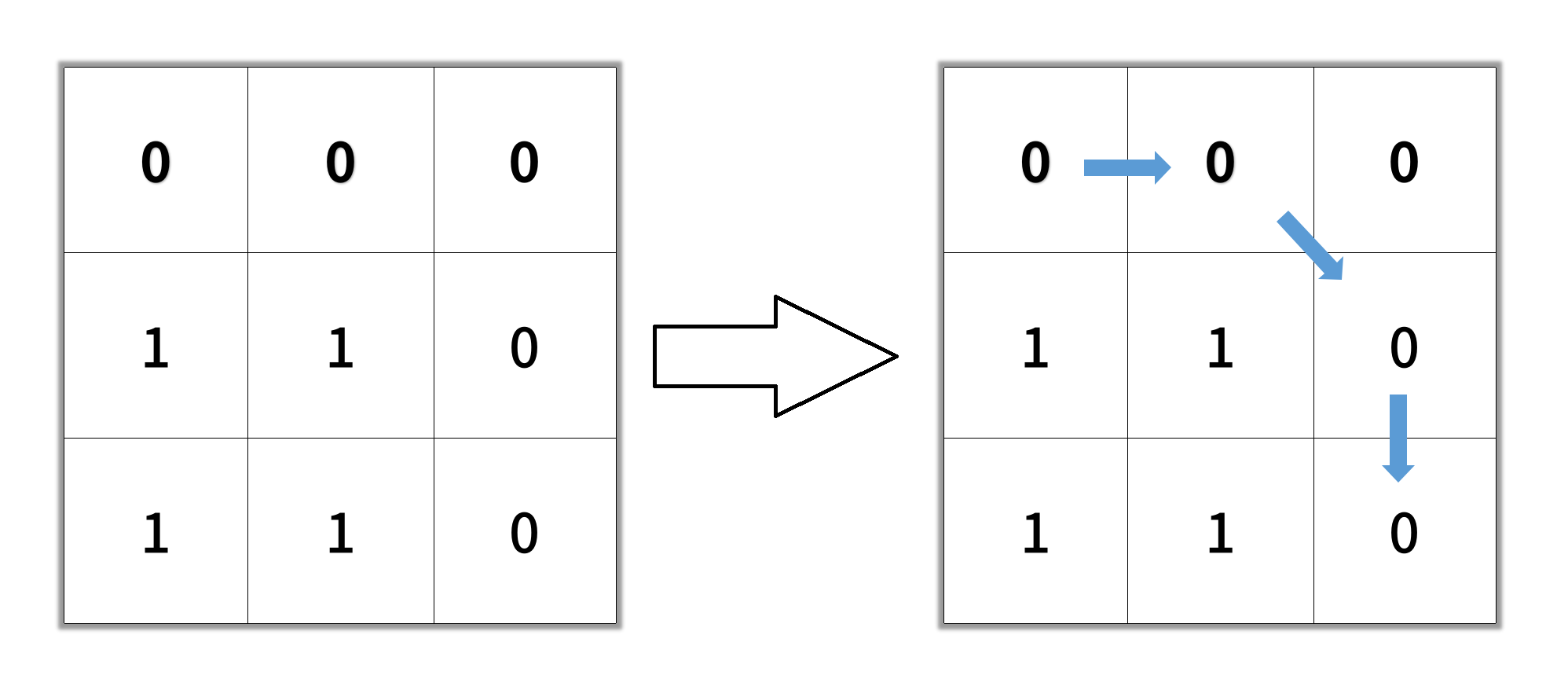
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

广度优先搜索解法：

畅通路径中，所有单元格的值必须为 0 且需要从 grid 左上角抵达右下角，同时本题另一个特殊之处在于需要考虑对角线在内的 8 个前进方向，而不是常规情况下的 4 个方向。

根据畅通路径的条件，首先进行简单判断：若左上或右下单元格值为1，不存在畅通路径；若矩阵大小为 1×1 且其中单个元素为 0，畅通路径即为 1，即仅经过 (0, 0) 位置一个点。

题目要求寻找最短的畅通路径长度，适合使用广度优先搜索，同时尝试所有可能的情况，只要一种情况下到达路径重点，该情况即为最短畅通路径的情况。而深度优先搜索是每次完成一条路径的搜索，要想得到最短畅通路径需要完成所有可能路径的搜索后取最小，因此使用 BFS 更加高效。

使用队列完成广度优先搜索，起点 (0, 0) 首先入队，路径值为 1；对当前队列中的每个节点，判断其通过 8 个方向走到下一步后的位置，若下一步的位置即为终点，路径值加一并直接返回路径值即为最小的畅通路径长度；否则仍然需要继续判断下一个位置是否仍在矩阵内且其值为 0，若是则将下一个位置添加到队列中待后续搜索使用，需要将加入队列的位置处的值改为 1 以避免重复搜索同一个位置；对队列中现有元素的处理过程中，如果队列中某个位置的下一个位置符合继续搜索的条件，需要将当前路径长度加 1，通过 flag 进行记录，只要有一个位置的下一个位置符合条件，当前路径长度就需要加 1。

如果在搜索过程中到达终点位置，路径长度加 1 后直接返回；若正常退出广度优先搜索过程，代表不存在符合条件的畅通路径，返回 -1。

class Solution {
public:
    int directions[8][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        if(grid[0][0] == 1 || grid[n - 1][n - 1] == 1)
            return -1;
        if(n == 1 && grid[0][0] == 0)
            return 1; 
        queue<pair<int, int>> que;
        que.push({0, 0});
        grid[0][0] = 1;
        int ans = 1;
        while(!que.empty()){
            int size = que.size();
            bool flag = false;
            for(int i = 0; i < size; i++){
                auto p = que.front();
                que.pop();
                for(auto direction: directions){
                    int x = p.first + direction[0], y = p.second + direction[1];
                    if(x == n - 1 && y == n - 1){
                        ans++;
                        return ans;
                    }
                    if(x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0){
                        que.push({x, y});
                        grid[x][y] = 1;
                        flag = true;
                    }
                }
            }
            if(flag)
                ans++;
        }
        return -1;
    }
};