二叉树的相关操作_abd空空空c空空二叉树-优快云博客

本文链接：https://blog.youkuaiyun.com/Nessie_zhao/article/details/80229375

本文详细介绍了二叉树的各种操作，包括从先序遍历结果创建二叉树、克隆二叉树、销毁二叉树、计算节点数量、叶子节点数量、第K层节点数、树的高度、判断节点是否存在以及查找节点的父节点。通过实例代码和测试结果展示每种操作的实现过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二叉树的遍历在前文二叉树的基本操作已经提到，接下来再分享一些二叉树的其他操作
1.二叉树的创建
给一个二叉树的先序遍历结果，空节点用”#”表示，然后进行创建
这里写图片描述
实现代码：

TreeNode* CreateTreeNode(TreeNodeType value)
{
    TreeNode* new_node = (TreeNode*)malloc(sizeof(TreeNode));
    new_node->data = value;
    new_node->lchild = NULL;
    new_node->rchild = NULL;
    return new_node;
}
TreeNode* _TreeCreate(TreeNodeType data[],size_t size,size_t* index,TreeNodeType null_node)
{
    if(index == NULL)
    {
        return NULL;
    }
    if((*index) >= size)
    {
        return NULL;
    }
    if(data[*index] == null_node)
    {
        return NULL;
    }
    TreeNode* new_node = CreateTreeNode(data[*index]);
    ++(*index);
    new_node->lchild = _TreeCreate(data,size,index,null_node);
    ++(*index);
    new_node->rchild = _TreeCreate(data,size,index,null_node);
    return new_node;
}
TreeNode* TreeCreate(TreeNodeType data[],size_t size,char null_node)
{
    size_t index = 0;//表示当前取数组的哪个元素
    return _TreeCreate(data,size,&index,null_node);
}

测试代码：

void TestCreate()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    printf("\n先序遍历：");
    TreePreOrder(root);
    printf("\n中序遍历：");
    TreeInOrder(root);
    printf("\n后序遍历：");
    TreePostOrder(root);
    printf("\n层序遍历：");
    TreeLevelOrder(root);
    printf("\n");
    return;
}

运行结果：
这里写图片描述
2.克隆一个二叉树
给一个二叉树，克隆出来一个一模一样的二叉树
这里需要解释一下：一般的Clone为深拷贝，Copy为浅拷贝
那么深浅拷贝的区别又是什么呢？？
浅拷贝只是增加了一个指针指向已经存在的内存，而深拷贝就是增加一个指针并且申请一个新的内存，使这个增加的指针指向这个新的内存，采用深拷贝的情况下，释放内存的时候就不会出现在浅拷贝时重复释放同一内存的错误！
这里写图片描述
实现代码：

TreeNode* TreeClone(TreeNode* root)
{
    if(root == NULL)
    {
        return NULL;
    }
    TreeNode* new_node = CreateTreeNode(root->data);
    new_node->lchild = TreeClone(root->lchild);
    new_node->rchild = TreeClone(root->rchild);
    return new_node;
}

测试代码：

void TestClone()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    TreeNode* new_root = TreeClone(root);
    printf("\n先序遍历：");
    TreePreOrder(new_root);
    printf("\n中序遍历：");
    TreeInOrder(new_root);
    printf("\n后序遍历：");
    TreePostOrder(new_root);
    printf("\n层序遍历：");
    TreeLevelOrder(new_root);
    printf("\n");
    return;
}

运行结果：
这里写图片描述
3.二叉树的销毁
实现代码：

void TreeDestroy(TreeNode* root)
{
    if(root == NULL)
    {
        //空树
        return;
    }
    TreeDestroy(root->lchild);
    TreeDestroy(root->rchild);
    DestroyTreeNode(root);
    return;
}

测试代码：

void TestDestroy()
{
    TEST_HEADER;
    TreeNode* a = CreateTreeNode('a');
    TreeNode* b = CreateTreeNode('b');
    TreeNode* c = CreateTreeNode('c');
    TreeNode* d = CreateTreeNode('d');
    TreeNode* e = CreateTreeNode('e');
    TreeNode* f = CreateTreeNode('f');
    TreeNode* g = CreateTreeNode('g');
    a->lchild = b;
    a->rchild = c;
    b->lchild = d;
    b->rchild = e;
    e->lchild = g;
    c->lchild = f;
    TreeDestroy(a);
    return;
}

4.求一个树有多少节点
这里有两种递归调用的方法，有各自的好处，方法一比较容易想，较为直观，方法二代码比较少，但是不太直观
实现代码：

//方法一
void _TreeSize(TreeNode* root,size_t* size)
{
    if(root == NULL || size == NULL)
    {
        return;
    }
    ++(*size);
    _TreeSize(root->lchild,size);
    _TreeSize(root->rchild,size);
}
size_t TreeSize1(TreeNode* root)
{
    size_t size = 0;
    _TreeSize(root,&size);
    return size;
}
//方法二
size_t TreeSize2(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + TreeSize2(root->lchild) + TreeSize2(root->rchild);
}

测试代码：

void TestSize1()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    size_t size = TreeSize1(root);
    printf("size: expected is 7, actual %lu\n",size);
}
void TestSize2()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    size_t size = TreeSize2(root);
    printf("size: expected is 7, actual %lu\n",size);
}

运行结果：
这里写图片描述
5.求一个树有多少个叶子节点
首先解释一下什么是叶子节点：没有子节点的节点交叶子节点，叶子节点是度为0的节点

实现代码：

size_t TreeLeafSize(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    if(root->lchild == NULL && root->rchild == NULL)
    {
        return 1;
    }
    return TreeLeafSize(root->lchild) + TreeLeafSize(root->rchild);
}

测试代码：

void TestLeafSize()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    size_t size = TreeLeafSize(root);
    printf("size: expected is 3, actual %lu\n",size);
}

运行结果：
这里写图片描述
6.求一个二叉树第K层节点的个数

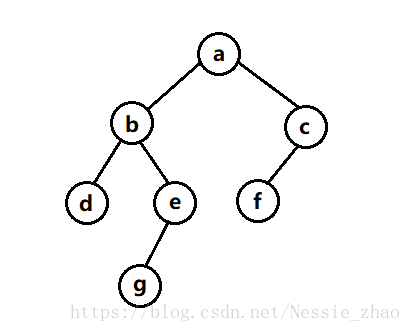
思想：如果想要求A的第3层，那就先求A左子树的第2层+A右子树的第二层
再求B左子树的第一层+B右子树的第一层+C左子树的第一层+C右子树的第一层
实现代码：

size_t TreeKLevelSize(TreeNode* root,int K)
{
    if(root == NULL || K < 1)
    {
        return 0;
    }
    if(K == 1)
    {
        return 1;
    }
    return TreeKLevelSize(root->lchild,K-1) + TreeKLevelSize(root->rchild,K-1);
}
size_t TreeHeight(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    size_t lheight = TreeHeight(root->lchild);
    size_t rheight = TreeHeight(root->rchild);
    return 1 + (lheight > rheight ? lheight : rheight);
}

测试代码：

void TestKLevelSize()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    size_t size = TreeKLevelSize(root,3);
    printf("size: expected is 3,actual %lu\n",size);
}

运行结果：
这里写图片描述
7.求一个二叉树的高度

先递归的求出左、右子树的高度，谁的高就用谁的+1就是整个书的高度
实现代码：

size_t TreeHeight(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    size_t lheight = TreeHeight(root->lchild);
    size_t rheight = TreeHeight(root->rchild);
    return 1 + (lheight > rheight ? lheight : rheight);
}

测试代码：

void TestHeight()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    size_t size = TreeHeight(root);
    printf("size: expected is 4 ,actual %lu\n",size);
}

运行结果：
这里写图片描述
8.判断一个节点是否在二叉树中
给出一个想要查找的值，求出相应节点的指针
实现代码：

TreeNode* TreeNodeFind(TreeNode* root,TreeNodeType to_find)
{
    if(root == NULL)
    {
        return NULL;
    }
    if(root->data == to_find)
    {
        return root;
    }
    TreeNode* lnode = TreeNodeFind(root->lchild,to_find);
    TreeNode* rnode = TreeNodeFind(root->rchild,to_find);
    return lnode != NULL ? lnode : rnode;
}

测试代码：

void TestNodeFind()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    TreeNode* node = TreeNodeFind(root,'g');
    printf("node: expected is %p,actual %p\n",root->lchild->rchild->lchild,node);
}

运行结果：
这里写图片描述
9.查找一个节点的父节点
实现代码：

TreeNode* TreeParent(TreeNode* root,TreeNode* child)
{
    if(root == NULL)
    {
        //空树
        return NULL;
    }
    if(child == NULL)
    {
        //非法输入
        return NULL;
    }
    if(root->lchild == child || root->rchild == child)
    {
        return root;
    }
    TreeNode* lnode = TreeParent(root->lchild,child);
    TreeNode* rnode = TreeParent(root->rchild,child);
    return lnode != NULL ? lnode : rnode;
}

测试代码：

void TestParent()
{
    TEST_HEADER;
    TreeNodeType data[] = "abd##eg###c#f##";
    TreeNode* root = TreeCreate(data,sizeof(data)/sizeof(data[0])-1,'#');
    TreeNode* child = root->lchild->rchild;
    TreeNode* node = TreeParent(root,child);
    printf("node: expected is %p,actual %p\n",root->lchild,node);
}

运行结果：
这里写图片描述