二叉树的相关操作（上）

本文章主要介绍二叉树的概念、特点、以及二叉树的相关操作。

1.二叉树的概念

一棵二叉树时节点的有限集合，该二叉树或者为空树、或者为只有一个根节点的树、或者为一个根节点有左右子树的树。总之，二叉树的每个节点最多有两个子树。下面画图表示二叉树的几种情况：

2. 二叉树的特点

（1）二叉树是递归定义的；

（2）二叉树的每个节点最多有两个子树即二叉树的度均不大于2；

（3）二叉树的子树有左右之分，其左右子树的次序不能颠倒。

3. 二叉树的相关操作

首先，怎么表示一棵树呢？我们可以类似于链表的形式，将一个指针变量的指向表示一棵树。然后，如何存储二叉树的节点呢？由于二叉树的特点：每个节点最多只有两个子树，故可以将二叉树每个节点的结构体设置为存放当前节点的元素，以及当前节点的左右子树的指向。依据这样的分析，写出关于二叉树的头文件tree.h如下：

//头文件只被编译一次
#pragma once
//宏定义一个标识符，用于测试时打印函数名
#define HEADER printf("================%s===============\n",__FUNCTION__)
//自定义树节点的数据类型，方便用户修改树节点的数据类型，默认设置为char类型
typedef char TreeNodeType;
//使用孩子表示法来表示树节点
typedef struct TreeNode{
    //存储树节点的元素
    TreeNodeType data;
    //存储树节点的左子树的指向
    struct TreeNode* lchild;
    //存储树节点的右子树的指向
    struct TreeNode* rchild;
}TreeNode;

3.1 二叉树的初始化、销毁节点、创建节点

初始化：既然是以一个指针变量的指向表示一棵二叉树，那么二叉树的初始化即将指针变量的指向置为空，初始化为一棵空二叉树。

//1.初始化
//思路：由于是使用根节点的指针表示一棵树，所以将根节点的指针置为NULL即表示初始化二叉树为空树
void TreeInit(TreeNode** proot)
{
    //非法判断
    if(proot==NULL)
    {
        return;                                                                                                          
    }
    //将根节点的指针置为NULL
    *proot=NULL;
}

销毁节点：销毁一个节点，相当于释放掉申请的内存空间，即使用free即可。

//2.销毁节点
//思路：直接将节点的指向释放                                                                                             
void DestroyTreeNode(TreeNode* node)
{
    free(node);
}

创建节点：先申请一块新内存，用于存放二叉树节点信息；再将节点的data域置为传入的参数值；3.最后，由于不知道该节点的左右子树是谁，所以暂且将该节点的左右子树的指向置为空。

//3.创建节点
//思路：将元素值赋值给节点的data，并将节点的lchild和rchild置为NULL
TreeNode* CreateTreeNode(TreeNodeType value)
{
    //动态申请新节点的内存
    TreeNode* new_node=(TreeNode*)malloc(sizeof(TreeNode));
    //给new_node的data赋值
    new_node->data=value;
    //给new_node的lchild和rchild置为NULL
    new_node->lchild=NULL;
    new_node->rchild=NULL;                                                                                               
    //返回创建的新节点的指向
    return new_node;
}

3.2 关于二叉树的遍历：先序遍历、中序遍历、后序遍历、层序遍历

1.先序遍历

遍历的顺序为根左右，具体操作分析如下：

（1）a这棵树，先访问根节点a，再访问a的左子树b（左边红色框内为a的左子树）

（2）b这棵树，先访问根节点b，再访问b的左子树d（左边绿色框内为b的左子树）

（3）d这棵树，先访问根节点d，d没有左右子树，所以根据根左右顺序，访问b这棵树的右子树e（右边绿色框内为b的右子树）

（4）e这棵树，先访访问根节点e，再访问e的左子树g（左边紫色框内为e的左子树）

（5）g这棵树，先访问根节点g，g没有左右子树，所以根据根左右顺序，访问a这棵树的右子树c（右边红色框内为a的右子树）

（6）c这棵树，先访问根节点c，c没有左子树，所以根据根左右的顺序，访问c这棵树的右子树f（右边蓝色框内为c的右子树）

（7）f这棵树，先访问根节点f，f没有左右子树，所以根据根左右顺序，整个二叉树访问完毕！

故，先序遍历的结果为：a b d e g c f

代码实现如下所示：

//思路：根左右的顺序去访问
//1.先访问根节点
//2.递归遍历左子树
//3.递归遍历右子树
void TreePreOrder(TreeNode* root)
{                                                                                                                        
    //空树
    if(root==NULL)
    {
        return;
    }
    //1.先访问根节点
    printf("%c ",root->data);
    //2.递归遍历左子树
    TreePreOrder(root->lchild);
    //3.递归遍历右子树
    TreePreOrder(root->rchild);
}

2.中序遍历

遍历的顺序为左根右，具体操作分析如下：

（1）a这棵树，先访问a的左子树b（左边红色框内为a的左子树b）

（2）b这棵树，先访问b的左子树d（左边绿色框内为b的左子树d）

（3）d这棵树，没有左子树，所以根据左根右顺序，访问d这棵树的根节点d，又d没有右子树，所以再访问b这棵树

（4）b这棵树，访问过左子树后，根据左根右顺序，再访问b这棵树的根节点b，再访问b的右子树

（5）b这棵树，访问过左子树和根节点后，根据左根右的顺序，再访问b这棵树的右子树e（右边绿色框内为b的右子树e）

（6）e这棵树，先访问e的左子树g（左边紫色框内为e的左子树g）

（7）g这棵树，由于没有左子树，根据左根右顺序，访问g的根节点g，又g也没有右子树，所以g访问完了继续访问e这棵树

（8）e这棵树，访问过e的左子树，根据左根右顺序，再访问e的根节点e，又e没有右子树，所以e访问完了继续访问b这棵树，又由于b这棵树也访问完了，所以继续访问a这棵树

（9）a这棵树，访问过a的左子树，根据左根右顺序，访问a的根节点a，再访问a的右子树c（右边红色框内为a的右子树c）

（10）c这棵树，由于c没有左子树，根据左根右顺序，所以访问c的根节点c，再访问c的右子树f（右边蓝色框内为c的右子树f）

（11）f这棵树，由于没有左子树，根据左根右顺序，所以访问f的根节点f，又f也没有右子树，所以f访问完了继续访问a这棵树，又a这棵树也访问完了，所以整个二叉树访问完毕！

故，中序遍历的结果为：d b g e a c f 

代码实现如下所示：

//5.树的中序遍历
//思路：左根右的顺序去访问
//1.递归遍历左子树
//2.访问根节点
//3.递归遍历右子树
void TreeInOrder(TreeNode* root)
{
    //空树
    if(root==NULL)
    {
        return;
    }
    //1.递归遍历左子树                                                                                                   
    TreeInOrder(root->lchild);
    //2.访问根节点
    printf("%c ",root->data);
    //3.递归遍历右子树
    TreeInOrder(root->rchild);
}

3.后序遍历

遍历的顺序为左右根，具体操作分析如下：

（1）a这棵树，根据左右根顺序，先访问a的左子树b（左边红色框内为a的左子树b）

（2）b这棵树，根据左右根顺序，先访问b的左子树d（左边绿色框内为b的左子树d）

（3）d这棵树，由于d没有左右子树，所以访问d的根节点d，d访问完了继续访问b这棵树

（4）b这棵树，由于访问过b的左子树，根据左右根，所以再访问b的右子树e（右边绿色框内为b的右子树e）

（5）e这棵树，根据左右根顺序，先访问e的左子树g（左边紫色框内为e的左子树g）

（6）g这棵树，由于g没有左右子树，所以访问g的根节点g，g访问完了继续访问e这棵树

（7）e这棵树，根据左右根顺序且e没有右子树，所以访问e的根节点e，e访问完了继续访问b这棵树

（8）b这棵树，访问过了b的左右子树，根据左右根顺序，所以再访问b的根节点b，b这棵树访问完了继续访问a这棵树

（9）a这棵树，访问过了a的左子树，根据左右根顺序，再访问a的右子树c（右边红色框内为a的右子树c）

（10）c这棵树，由于c没有左子树，根据左右根顺序，访问c的右子树f（右边蓝色框内为c的右子树f）

（11）f这棵树，由于f没有左右子树，根据左右根顺序，所以访问f的根节点f，f访问完了继续访问c这棵树

（12）c这棵树，由于访问完了c的左右子树，根据左右根顺序，再访问c的根节点c，c访问完了继续访问a这棵树

（13）a这棵树，由于访问过了c的左右子树，根据左右根顺序，再访问a的根节点a，a访问完即整个二叉树访问完毕！

故，后序遍历的结果为：d g e b f c a

代码实现如下所示：

//6.树的后序遍历
//思路：左右根的顺序去访问
//1.递归遍历左子树
//2.递归遍历右子树
//3.访问根节点
void TreePostOrder(TreeNode* root)
{
    //空树
    if(root==NULL)
    {
        return;
    }
    //1.递归遍历左子树                                                                                                   
    TreePostOrder(root->lchild);
    //2.递归遍历右子树
    TreePostOrder(root->rchild);
    //3.访问根节点
    printf("%c ",root->data);
}

4.层序遍历

遍历的顺序为一层一层的遍历，具体操作分析如下：

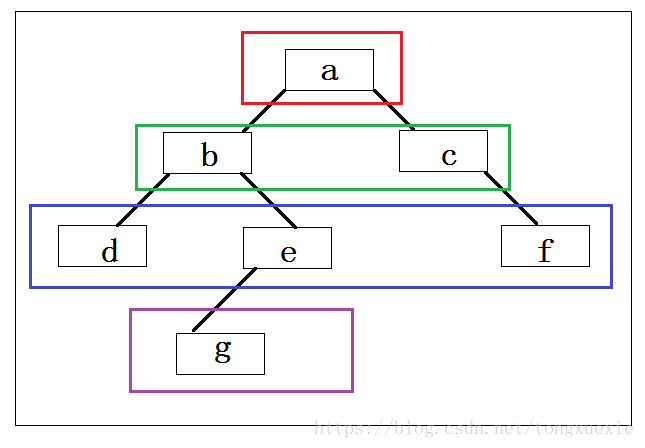
（1）从左向右访问第一层（红色框内为第一层），故先访问a

（2）从左向右访问第二层（绿色框内为第二层），故再访问b c

（3）从左向右访问第三层（蓝色框内为第三层），故再访问d e f

（4）从左向右访问第四层（紫色框内为第四层），故最后访问g

故，层序遍历的结果为：a b c d e f g 

那代码实现要怎么实现呢？仅仅通过观察层数来层序遍历二叉树是不能够用代码实现的，我们可以利用队列来帮助我们实现层序遍历的代码。整体思路如下：

（1）既然要利用队列，就会用到队列的入队列、出队列、取队首元素的操作

（2）首先，将二叉树的根节点入队列、取队首元素并出队列

（3）将出队列的根节点的左右子树依次入队列

（4）取当前队列的队首元素并出队列，再将出队列的节点的左右子树依次入队列

（5）再循环执行第四步

//7.树的层序遍历
//思路：借助队列
//1.将根节点入队列，取队首元素并出队列
//2.将1步中出队列的节点的左右子树入队列，取队首元素并出队列
//3.将2步中出队列的节点的左右子树入队列，取对手元素并出队列
//4.如此反复，总结为三步走战略：1.节点入队列 2.取队首元素并出队列 3.将出队列的节点的左右子树入队列
void TreeLevelOrder(TreeNode* root)
{
    //空树
    if(root==NULL)
    {   
        return;
    }                                                                                                                    
    //创建队列并初始化
    SeqQueue queue;
    SeqQueueInit(&queue);
    //1.将根节点入队列
    SeqQueuePush(&queue,root);
 //循环执行取队首元素出队列入队列操作
    while(1)
    {
        //2.取队首元素
        SeqQueueType front;
        int ret=SeqQueueFront(&queue,&front);
        //若取队首元素失败，则队列为空；若队列为空，则循环结束
        if(ret==0)
        {
            return;
        }
        //3.打印当前队首元素的data
        printf("%c ",front->data);                                                                                       
        //4.出队列
        SeqQueuePop(&queue);
        //5.将出队列的节点的左右子树入队列
        if(front->lchild!=NULL)
        {
 SeqQueuePush(&queue,front->lchild);
        }
        if(front->rchild!=NULL)
        {
            SeqQueuePush(&queue,front->rchild);
        }                                                                                                                
    }
}

注：以上代码用到的关于队列的相关操作，需要用到我的博客：https://blog.youkuaiyun.com/tongxuexie/article/details/79858973中的关于顺序表实现队列的入队列、出队列、取队首元素的操作！但需要注意的是，之前的队列元素的数据类型为char，现在需要改为二叉树节点的结构体类型TreeNode*。这里就不再添加关于队列的代码！自行修改实现！

3.3 创建二叉树

要求：通过一个数组，该数组中的元素内容符合二叉树的先序遍历后的结果，且该数组中元素不仅仅有非空子树的元素，还有空子树的元素，而空子树的元素是什么可以自行定义，但不要和非空子树的元素发生冲突！

创建树的思路如下：

（1）依然利用的是递归的思想创建二叉树

（2）定义一个变量index，用于表示数组索引值，递归时，通过传入index的地址去统一改变index的指向，从而访问数组的元素

（3）先根据index指向的内容，创建一棵树

（4）再将index++，递归创建这棵树的左子树

（5）再将index++，递归创建这棵树的右子树

（6）递归执行第三、四、五步，从而利用一个数组创建一棵树

（7）递归出口为index超出的数组的大小size时，返回NULL

代码实现如下所示：

//8.创建树
//思路：输入一个数组，根据数组的内容构建一棵树，数组中的元素符合树的先序遍历且包括空子树
//传入三个参数：1.数组 2.数组的大小 3.设置空子树的元素
//1.index表示数组的索引值，根据index指向的内容，创建一棵树
//2.index++后递归创建新节点的左子树                                                                                                  
//3.index++后递归创建新节点的右子树
TreeNode* CreateTree(TreeNodeType data[],size_t size,TreeNodeType null_type)
{
    //定义变量，表示数组的索引值
    int index=0;
    //传入index的地址，便于统一使用访问数组的索引值index
    return _CreateTree(data,size,&index,null_type);
}
TreeNode* _CreateTree(TreeNodeType data[],size_t size,int* index,TreeNodeType null_type)
{
    //非法输入
    if(index==NULL)
    {
        return NULL;
    }
    //*index是否超出数组的合法范围
if(*index>=size)
    {
        return NULL;
    }
    //当索引值为*index的数组元素为空子树时，返回NULL
    if(data[*index]==null_type)
    {
        return NULL;
    }
    //1.创建根节点
    TreeNode* new_node=CreateTreeNode(data[*index]);
    //2.递归创建左子树
    ++(*index);
    new_node->lchild=_CreateTree(data,size,index,null_type);
    //3.递归创建右子树
    ++(*index);
    new_node->rchild=_CreateTree(data,size,index,null_type);                                                                         
    return new_node;
}

3.4 二叉树的拷贝与销毁

拷贝分为三种拷贝方式：1.浅拷贝 2.深拷贝 3.写时拷贝。下面以深拷贝的方式对二叉树进行拷贝

//9.树的拷贝
//思路：采用的是深拷贝，即重新分配内存
TreeNode* TreeClone(TreeNode* root)                                                                                                  
{
    //空树时返回NULL
    if(root==NULL)
    {
        return NULL;
    }
    //按照先序方式进行遍历
    TreeNode* new_node=CreateTreeNode(root->data);
    new_node->lchild=TreeClone(root->lchild);
    new_node->rchild=TreeClone(root->rchild);
    return new_node;
}

销毁的核心思想还是遍历，所以用什么方式遍历去销毁二叉树很重要！！！

（1）选择先序遍历去销毁二叉树时，需要注意，当你销毁了根节点后，需要知道根节点的左右子树后才能接着销毁二叉树的其他节点，所以要想用先序遍历的方式销毁二叉树，在销毁每一个节点前，需要先将节点的左右子树的指向保存。

（2）选择中序遍历去销毁二叉树的思想和上述一样。

（3）选择后序遍历销毁二叉树时，不需要另外保存节点的左右子树的指向，因为后序遍历的顺序是左右根，所以最后才会销毁根节点。

我选择利用后序遍历实现销毁二叉树，代码实现如下所示：

//10.树的销毁
//后序遍历去销毁树的每一个节点
void DestroyTree(TreeNode** proot)
{
    //非法输入
    if(proot==NULL)
    {
        return;
    }
    //空树
    if(*proot==NULL)
    {
        return;
    }
    //1.销毁左子树
    DestroyTree(&((*proot)->lchild));
    //销毁右子树                                                                                                                     
    DestroyTree(&((*proot)->rchild));
    //销毁当前根节点
    DestroyTreeNode(*proot);
    (*proot)=NULL;
}

3.5 关于二叉树的其他操作（代码中有详细的思路以供参考）

//11.求二叉树中节点个数
//思路1：利用计数器，每当遍历到一个节点，就对计数器++
size_t TreeSize(TreeNode* root)
{
    //定义计数器
    size_t size=0;
    //调用下面函数实现计数器++
    _TreeSize(root,&size);
    return size;
}
void _TreeSize(TreeNode* root,size_t* size)
{
    if(root==NULL)
    {
        return;
    }                                                                                                                                
    ++(*size);
    _TreeSize(root->lchild,size);
    _TreeSize(root->rchild,size);
}
//思路2：利用递归计算节点个数
size_t TreeSizeEx(TreeNode* root)
{
    //空树
    if(root==NULL)
    {
        return 0;
    }
    return 1+TreeSizeEx(root->lchild)+TreeSizeEx(root->rchild);
}
//12.求二叉树叶子节点个数
//利用递归，计算二叉树叶子结点个数相当于计算二叉树根节点的左右子树的叶子结点个数的和
size_t TreeLeafSize(TreeNode* root)
{
    //空树
    if(root==NULL)
    {
        return 0;                                                                                                                    
    }
    //左右子树都为空时，该节点为叶子节点
    if(root->lchild==NULL&&root->rchild==NULL)
    {
        return 1;
  }
    return TreeLeafSize(root->lchild)+TreeLeafSize(root->rchild);
}
//13.二叉树的第K层节点个数
//思路：递归思想 => 计算二叉树的第K层节点个数=1+二叉树的根节点的左子树的第K-1层节点个数+二叉树的根节点的右子树的第K-1层节点个数
size_t TreeKLevelSize(TreeNode* root,int k)
{
    //空树或者k不是合法范围时
    if(root==NULL||k<1)
    {
        return 0;
    }
    if(k==1)
    {
        return 1;
    }                                                                                                                                
    return TreeKLevelSize(root->lchild,k-1)+TreeKLevelSize(root->rchild,k-1);
}
//14.求二叉树的高度
//递归思想 => 计算二叉树的高度=1+二叉树根节点的左子树的高度+二叉树根节点的右子树的高度，递归下去
size_t TreeHeight(TreeNode* root)
{
    if(root==NULL)                                                                                                                   
    {
        return 0;
    }
    //当节点的左右子树为空时，高度+1
    if(root->lchild==NULL&&root->rchild==NULL)
    {
        return 1;
    }
    //递归计算左子树的高度
    size_t lheight=TreeHeight(root->lchild);
    //递归计算右子树的高度
    size_t rheight=TreeHeight(root->rchild);
    return 1+(lheight>rheight?lheight:rheight);
}
//15.在二叉树中查找节点
//思路：利用先序遍历查找节点
TreeNode* TreeFind(TreeNode* root,TreeNodeType to_find)
{
    //空树
    if(root==NULL)                                                                                                                   
    {
        return NULL;
    }
    if(root->data==to_find)
    {
        return root;
    }
    //在根节点的左子树中查找
    TreeNode* lresult=TreeFind(root->lchild,to_find);
    //在根节点的右子树中查找
    TreeNode* rresult=TreeFind(root->rchild,to_find);
    //非空的子树为要查找的节点
    return lresult!=NULL?lresult:rresult;
}
//16.求父节点
TreeNode* Parent(TreeNode* root,TreeNode* child)
{
    //空树或非法输入
    if(root==NULL||child==NULL)
    {                                                                                                                                
        return NULL;
    }
    //当节点的左子树或右子树==child时，即找到了父节点
    if(root->lchild==child||root->rchild==child)
    {
        return root;
    }
    //在节点的左子树中继续寻找父节点
    TreeNode* lresult=Parent(root->lchild,child);
    //在节点的右子树中继续寻找父节点
    TreeNode* rresult=Parent(root->rchild,child);
    //非空的子树为要查找的父节点
    return lresult!=NULL?lresult:rresult;
}
//17.求左子树
TreeNode* LChild(TreeNode* root)
{
    //空树
    if(root==NULL)
    {                                                                                                                                
        return NULL;
    }
    return root->lchild;
}
//18.求右子树
TreeNode* RChild(TreeNode* root)
{
    //空树
    if(root==NULL)
    {
        return NULL;
    }
    return root->rchild;
}