2021牛客暑期多校训练营3-B题

最新推荐文章于 2026-01-07 11:46:22 发布

原创最新推荐文章于 2026-01-07 11:46:22 发布 · 274 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++

针对一个n行m列的白色棋盘，通过特殊才能降低染黑成本的问题，利用图论和最小生成树算法找到了最优解决方案。

B题:Black and white

原题链接：https://ac.nowcoder.com/acm/contest/11254/B

题目大意

Goodeat有一个n行m列的白色的棋盘。每个网格(i, j)都有一个权重c(i, j)。在任何时候，网格(i, j)都可以用c(i, j)的代价染成黑色。
Goodeat有一种特殊的才能。对于任意两行两列的四个相交的正方形，如果其中三个是黑色正方形，Goodeat可以免费将第四个正方形染成黑色。
请找出染色黑色棋盘的最低成本。

思路

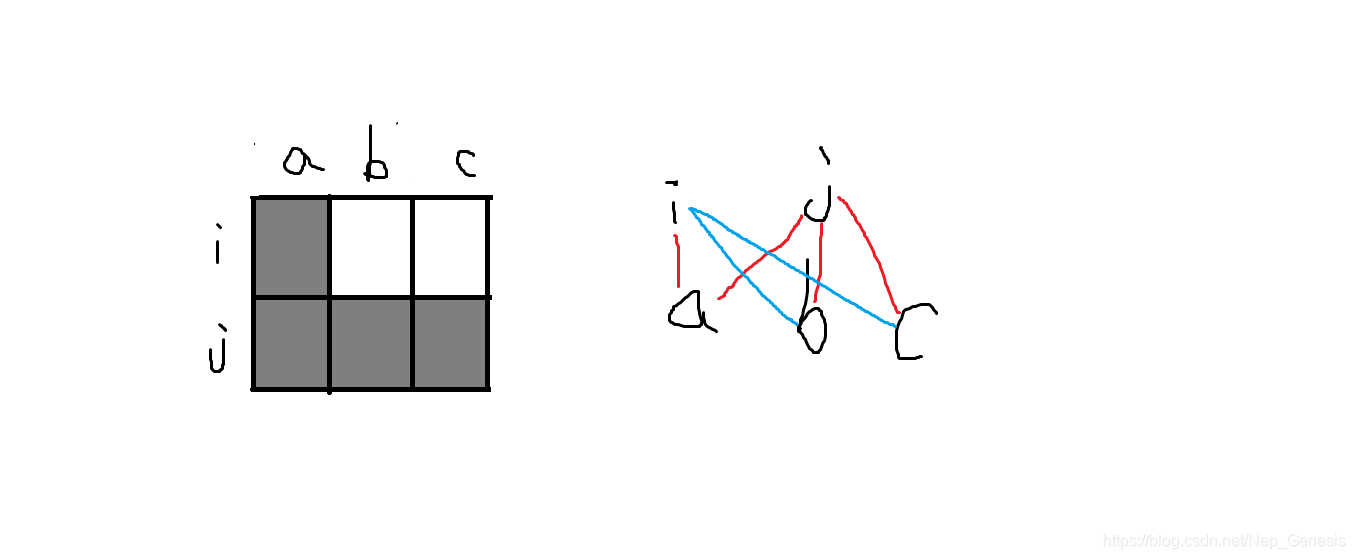
将每个格点的横纵坐标看做点，格点若已上色，则两点之间有一条边直接相连。Goodeat的特殊才能从下图中可以看出，如果其中三个是黑色正方形，第四个正方形是免费上色，也就是当两点间接相连，是0代价上色。将所有格点上色的最低成本就可以转化成求所有点直接或间接相连的最小代价，用最小生成树即可解决。
在这里插入图片描述

代码实现

#include<bits/stdc++.h>
#define ll long long
using namespace std;
struct node
{
	int x,y;
};
ll a,b,c,d,p,ans=0;
int n,m;
int f[101010];
int sf(int x){
	return x==f[x]?f[x]:f[x]=sf(f[x]);
}
vector<node> v[100010];
int main()
{
	scanf("%d%d%lld%lld%lld%lld%lld",&n,&m,&a,&b,&c,&d,&p);
	ll value=a;
	for(int i=1; i<=n+m; i++) f[i]=i;
	for(int i=1; i<=n; i++)
	{
		for(int j=1; j<=m; j++)
		{
			value=(value*value*b+value*c+d)%p;
			v[value].push_back(node {i,n+j});
		}
	}
	for(int i=0; i<=100000; i++)
	{
		for(auto j:v[i])
		{
			int x=sf(j.x),y=sf(j.y);
			if(x!=y){
				ans+=i;
				f[x]=y;
			}
		}
	}
	printf("%lld\n",ans);
}