常见排序算法

 /懂了和写出来是两码事啊啊......orz./

Talk is cheap, show me the code

一、快速排序

直接背模板就能过：

当x=q[l+r>>1]的边界情况
此时x取的是序列中间靠左的位置(如果序列个数为奇,则取正中间,如果为偶,则取中间靠左),此时如果元素个数为2,
则中间靠左就是第1个元素,这时就跟x=q[l]的边界情况一致了,所以这时只能用sort(l,j),sort(j+1,r);

AcWing 785. 快速排序 - AcWing

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1e5 +10;
int q[N],n;
void quick_sort(int l,int r)
{
    if(l>=r) return; //数组中只有一个或数组为空
    int x = q[l+r>>1];
    int i =l-1,j=r+1;
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    quick_sort(l,j);
    quick_sort(j+1,r);//此处是边界处理
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&q[i]);
    quick_sort(0,n-1);
    for(int i =0;i<n;i++) printf("%d ",q[i]);
    return 0;
}

扩展：第K个数活动 - AcWing

多家了一步，判断第k个数是在左边还是在右边，

在左边：区间长度，j-l+1>k,开始，l,结束，j，在区间中第k个数。

在右边：区间长度，j-l+1<k,开始，j+1,结束，r，在区间中第k -（j-l+1）个数。

#include <iostream>
using namespace std;
const int N = 1000010;
int q[N];

//返回值是int
int quick_sort(int q[],int l,int r,int k)//要写int q[]
{
    if(l>=r) return q[l];
    int i=l-1,j=r+1,x=q[(l+r)>>1];
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    if(j-l+1>=k) return quick_sort(q,l,j,k);
    else return quick_sort(q,j+1,r,k-(j-l+1));
    //判断k与j的大小，如果在左边就返回左边的数
}
int main()
{
    int n,k;
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i ++ ) scanf("%d",&q[i]);
    cout << quick_sort(q,0,n-1,k)<<endl;
    return 0;
}

时间复杂度：

最坏：逆序的

 二、归并排序

AcWing 787. 归并排序的证明与边界分析 - AcWing

时间复杂度：O(nlogn)

#include <iostream>
#include <cstring>
#include <algorithm>
const int N = 1e5+10;
int a[N],temp[N];
using namespace std;
void merge_sort(int q[],int l,int r)
{
    if(l>=r) return;
    int mid =(l+r)>>1;
    merge_sort(q,l,mid), merge_sort(q,mid+1,r);//递归时mid+1成为l
    
    int k =0,i=l,j=mid+1;
    while (i<=mid && j<=r)
    {
        if(q[i]<q[j]) temp[k++]=q[i++];
        else temp[k++] = q[j++];
    }
    while(i<=mid) temp[k++]=q[i++];
    while(j<=r) temp[k++]=q[j++];
    
    for(int i =l,j=0;i<=r;i++,j++) q[i] = temp[j];

}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d",&a[i]);
    merge_sort(a,0,n-1);
    for (int i = 0; i < n; i ++ ) printf("%d ",a[i]);
    
    return 0;
}

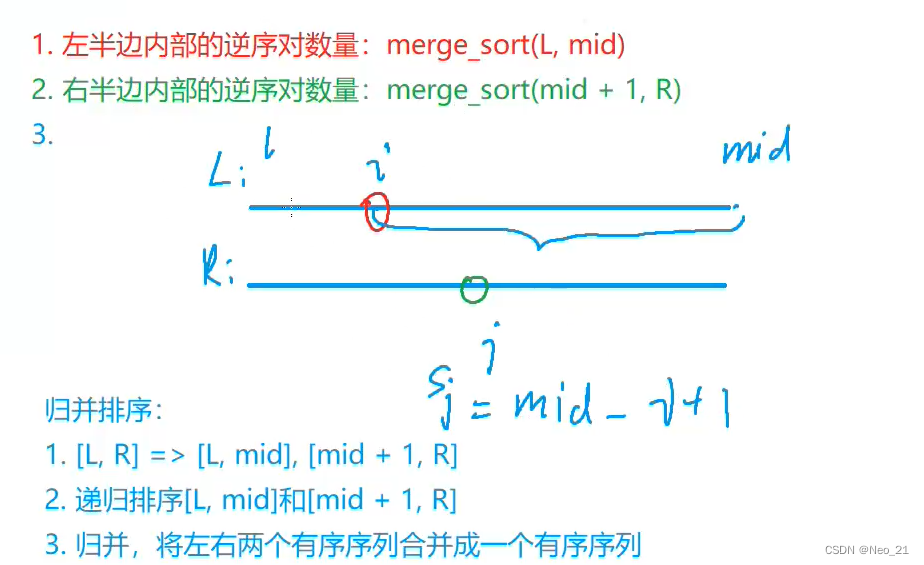
难一点的：求逆序对

基本思路：设置一个mid，先求左半边内部和右半边内部的逆序对的数量：直接求

（两个数同时出现在左半边，或同时出现在右半边）

然后再用归并的思想，左半边的指针i,右半边的指针j。此时左半边和右半边都是有序的（从小到大），如果（i，j）是一对逆序对，那么在左半边有mid-l+1个关于j的逆序对。

AcWing 788. 逆序对的数量-要点 - AcWing

#include<iostream>
using namespace std;
const int N=1e5+10;
int q[N], tmp[N];
int n;
typedef long long LL;

LL merge_sort(int l, int r){
    if(l>=r) return 0;
    LL s=0;

    int mid=l+r>>1;
    s=merge_sort(l, mid)+merge_sort(mid+1, r);

    int i=l, j=mid+1, k=0;
    while(i<=mid && j<=r){
        if(q[i]<=q[j]) tmp[k++]=q[i++];
        else {
            s+= mid-i+1;
            tmp[k++]=q[j++];
        }
    }
    while(i<=mid) tmp[k++]=q[i++];
    while(j<=r) tmp[k++]=q[j++];

    for(int i=l, k=0;i<=r;i++, k++) q[i]=tmp[k];
    return s;
}

int main(){
    cin>>n;
    for(int i=0;i<n;i++) scanf("%d", &q[i]);
    cout<<merge_sort(0, n-1) ;
    return 0;

}

 三、二分排序

整数二分

基本分治算法：AcWing 789. 二分算法的证明和边界分析 - AcWing

#include<iostream>
using namespace std;
const int N = 100010;
int n,m;//m个查询
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
    
    while (m -- )
    {
        int x;//输入要查询的数
        scanf("%d",&x);
        
        int l=0,r=n-1;
        while(l<r)//寻找右边分界点，保证右边界点一直大于或等于x，然后左边靠近（else）
        {
            int mid = l+r>>1;//向下取整
            if(q[mid]>=x) r = mid;//向左边缩小
            else l = mid+1;//向右边缩小
        }
        if(q[l]!=x) cout<<"-1 -1"<<endl;//不存在
        else
        {
            cout << l<<' ';//输出起始位置
            
            int l=0,r=n-1;
            while(l<r)//寻找左边分界点,保证左边界点一直小于或等于x,然后右边靠近
            {
                int mid = l+r+1>>1;//mid向上取整
                if(q[mid]<=x) l=mid;//
                else r =mid-1;
            }
            cout <<l <<endl;
        }
    }
    return 0;
}

循环终止时， l >= r

易知 l不可能比 r 大 , 故 l = r, 根据循环不变式，l 就是答案点 res

另一种方法：（推荐使用）不需要考虑mid+1、mid-1的二分查找模板，希望大家都能学会_一支彩色铅笔csdn_一支彩色铅笔的博客-优快云博客

时间复杂度：logn,因为指针每次移动都向边界移动

区域长度缩小一半。

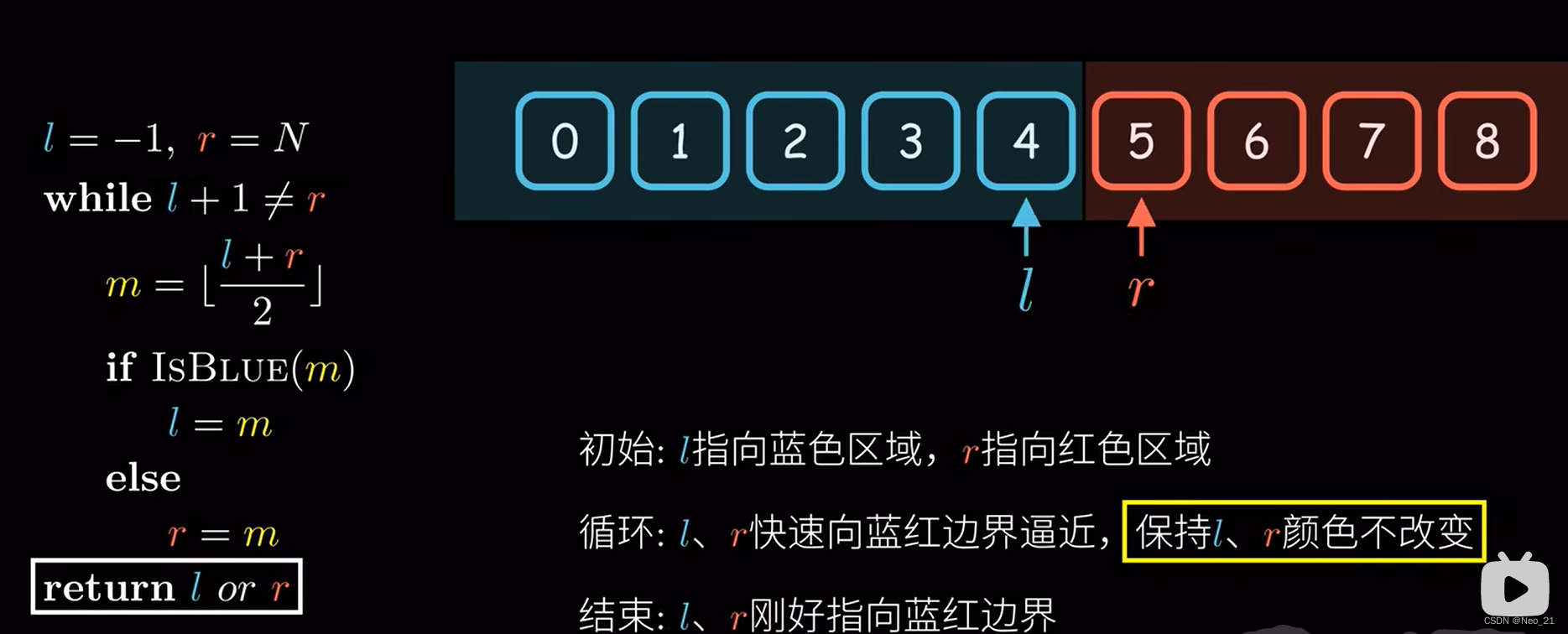
细节点：

1. 
2. 

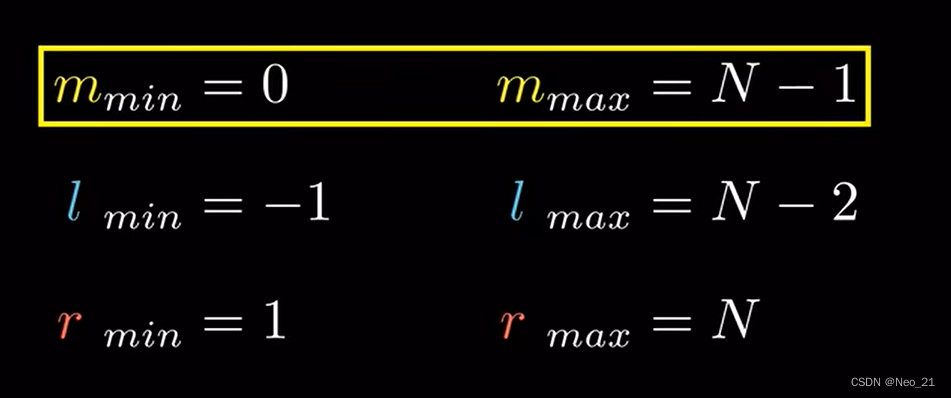fu

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,m,q[N];
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++) scanf("%d",&q[i]);
    while(m--)
    {
        int k;scanf("%d",&k);
        //寻找第一个等于K的坐标 我这边让二分的边界定为 左边为<5 右边>=5 则所求为r
        int l=-1,r=n;
        while(l+1!=r)//当l与r没有相接的时候,求边界
        {
            int mid=l+r>>1;
            //下面找第一个>=5的坐标
            if(q[mid]>=k) r=mid;
            else l=mid;
        }
        //此时得到的r是第一个>=5的坐标
        if(q[r]!=k) printf("-1 -1\n");
        else{
            printf("%d ",r);
                //现在找最后一个<=5的数字 我这边让二分的左边为<=5 右边为>5 则所求为ll
                int ll=-1,rr=n;
                while(ll+1!=rr)
                {
                    
                    int mid=ll+rr>>1;
                    if(q[mid]<=k) ll=mid;
                    else rr=mid;
                }
                if(q[ll]!=k) printf("%d\n",r);//终止位置和起始位置相同，只有一个这样的元素
                else printf("%d\n",ll);
            }
    }
    
}

浮点数二分： AcWing 790. 数的三次方根 - AcWing

注意精度：r-l>=1e-8 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

int main()
{
    double n;
    scanf("%lf", &n);
    double l = -10000, r = 10000;
    while (r - l >= 1e-8) //防止精度出错
    {
        double mid = (l + r) / 2;
        if (mid * mid * mid >= n) r = mid;
        else l = mid;
    }
    printf("%.6lf", l);
    return 0;
}