排序算法----堆排序

1. 堆排序：堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

2. 二叉堆的定义：二叉堆是一颗完全二叉树，堆中的某个结点的值总是不大于父节点的值，通常这种堆称为最大堆（相应的可以定义最小堆）。下层的某一元素不一定小于上层的某一元素，既然是完全二叉树，所以可以用数组定义该结构。

如图就是一个二叉堆：

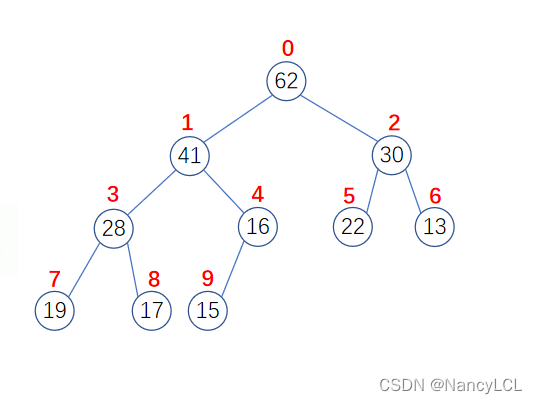
3. 堆中的节点关系：因为是通过数组进行存储的，所以节点的角标就对应数组中的角标。

        1>. 父节点角标：( 子节点角标 - 1 ) / 2。即" parent = ( i - 1 ) / 2 "。

        2>. 左孩子角标：父节点角标 * 2 + 1。即" leftChild = 2 * i + 1 "。

        3>. 右孩子角标：父节点角标 * 2 + 2。即" rightChild = 2 * i + 2 "。

 4. 堆排序的时间和空间复杂度即稳定性：

        1>. 时间复杂度：O(nlog2n) 。

        2>. 空间复杂度：O(1) 。

        3>. 稳定性： 不稳定。

5. 堆排序的实现：

//堆排序
public class HeapSort {
	public static void main(String[] args) {
		int[] arr = {3, 5, 2, 1, 4};
		heapSort(arr);
		System.out.println(Arrays.toString(arr));
	}

	private static void heapSort(int[] arr) {
		//先将数组最大堆化
		heapify(arr);
		
		//先将数组中的第一个元素与最后一个元素交换位置将最大元素交换到数组末尾 再继续堆化
		//但是继续堆化时就不需要再管最后的元素了
		int len = arr.length;
		for(int i = arr.length - 1; i >= 0; i--) {
			swap(arr, 0, i);
			len--;
			siftDown(arr, 0, len);
		}
	}

	//将数组最大堆化
	private static void heapify(int[] arr) {
		for(int i = arr.length - 1; i >= 0; i--) {
			//下沉指定位置的元素
			siftDown(arr, i, arr.length);
		}		
	}

	//在指定长度中下沉指定位置的元素
	private static void siftDown(int[] arr, int k, int len) {
		while(leftChild(k) < len) {
			int j = leftChild(k);
			if(j + 1 < len && arr[j + 1] > arr[j]) {
				j = rightChild(k);
			}
			if(arr[k] < arr[j]) {
				swap(arr, k, j);
				k = j;
			}else {
				break;
			}
		}
	}

	//交换两个指定位置的元素的位置
	private static void swap(int[] arr, int i, int j) {
		int temp = arr[i];
		arr[i] = arr[j];
		arr[j] = temp;
		
	}

	//获取指定位置元素的左孩子角标
	private static int leftChild(int index) {
		return index * 2 + 1;
	}
	
	//获取指定位置元素的右孩子角标
	private static int rightChild(int index) {
		return index * 2 + 2;
	}
}

6. 运行结果：