ComSec作业3

最新推荐文章于 2025-12-28 17:51:54 发布

原创

最新推荐文章于 2025-12-28 17:51:54 发布 · 294 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #网络安全

本文深入探讨RSA算法的原理，通过具体案例展示加密和解密过程，包括计算私钥、公钥，并解决实际的加密问题。同时，文章提供了详细计算步骤，帮助读者掌握RSA算法的应用。

1、为什么RSA算法加解密互逆？

在这里插入图片描述
$\begin{aligned} m&=c^dmod\:n\\ &=m^{ed}mod\:n\\ &=m^{k\lambda(n)+1}mod\:n\\ \\ m^{k\lambda(n)+1}mod\:p&=m^{k*l*(p-1)+1}mod\:p\\ &=m^{k*l*(p-1)}*m\:mod\:p\\ &=m\:mod\:p\\ \\ m^{k\lambda(n)+1}mod\:q&=m^{k*l*(q-1)+1}mod\:q\\ &=m^{k*l*(q-1)}*m\:mod\:q\\ &=m\:mod\:q\\ \\ m^{k\lambda(n)+1}mod\:n&=m\:mod\>pq \end{aligned}$

2、对下列数据实现加密和解密

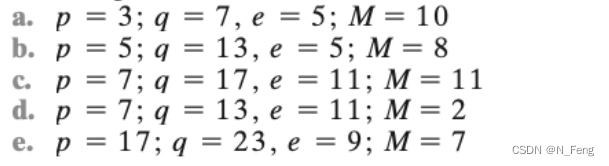
在这里插入图片描述

a.p = 3;q = 7,e = 5; M = 10

$\begin{aligned} n&=pq=21\\ \phi(n)&=(p-1)(q-1)=12\\ e&=5\\ ed&\equiv1mod(\phi(n))\\ 即5d&\equiv1mod(12) \end{aligned}$
用egcd算法有
$\begin{matrix} 0 & 1 & 12\\ 1 & 0 & 5 \\ -2 & 1 & 2\\ 5 & -2 & 1\\ \end{matrix} \tag{1}\\ 5\times5+(-2)\times12=1\\ 解得d=5$
$\begin{aligned} C=M^emodn&=10^5mod21\\ &=10\times10^4mod21\\ &=(10mod21\times10^4mod21)mod21\\ &=(10\times4)mod21\\ &=19\\ \\ M=C^dmodn&=19^5mod21\\ &=19\times19^4mod21\\ &=(19mod21\times19^4mod21)mod21\\ &=(19mod21\times(-2)^4mod21)mod21\\ &=(19\times16)mod21\\ &=10\\ \end{aligned}$