树状数组---板子题

原创

已于 2022-01-29 19:20:39 修改 · 350 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #排序算法

于 2020-12-12 20:26:06 首次发布

这篇博客介绍了树状数组在处理动态更新和区间查询问题中的应用，包括如何进行树状数组操作、计算逆序对数量以及矩阵变换。通过实例展示了如何使用树状数组解决这些经典算法问题。

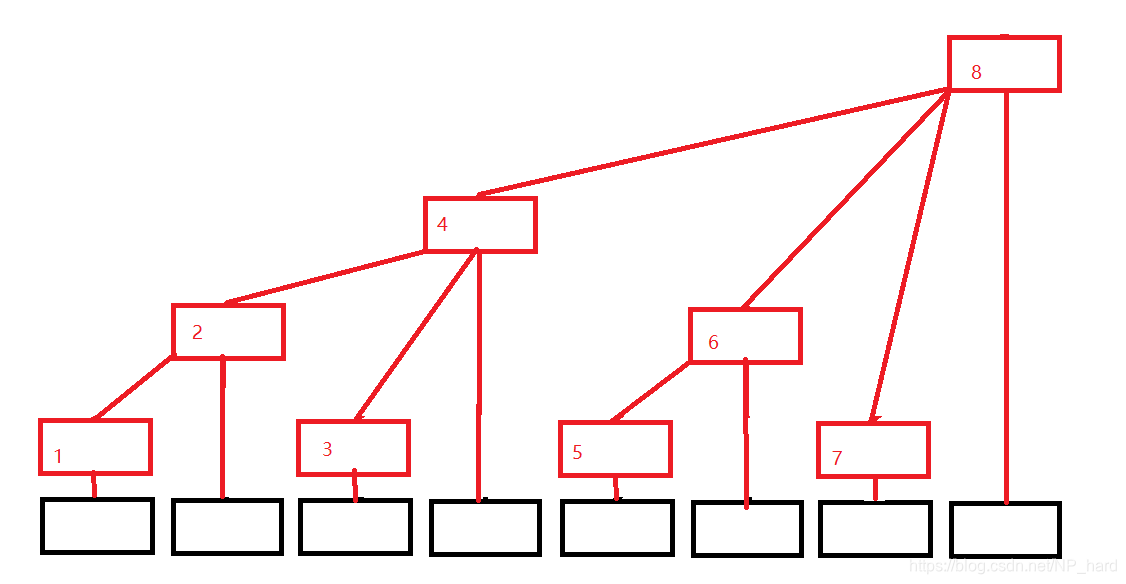
问题 A: 树状数组操作

题目描述

给你n个数，创建一个树状数组，并执行相应操作，按格式要求输出操作结果。执行的操作有以下两种形式：

C i dt ，表示更新A[i]，使得A[i]=A[i]+dt，其中1<=i<=n；

Q i j ，表示询问区间和，即A[i]+A[i+1]+…+A[j]的值，其中1<=i<=j<=n。

输入

第一行一个正整数n（1<=n<=10000），代表数据个数。

接下来一行是n个数据。

接下来一行一个正整数m，代表m个操作。

接下来m行，每行一个操作，格式如上所述。

输出

第一行输出创建后的树状数组，数据之间以空格分隔。

接下来m行，输出m个操作结果：对每个“C i dt ”操作，输出更新后的树状数组，数据间以空格分隔；对每个“Q i j ”操作，输出一个数值。

样例输入

10
1 3 2 6 7 -2 5 8 4 10
5
Q 1 10
C 2 4
Q 2 6
C 6 -3
Q 6 6

样例输出

1 4 2 12 7 5 5 30 4 14
44
1 8 2 16 7 5 5 34 4 14
20
1 8 2 16 7 2 5 31 4 14
-5

代码

#include<iostream>
#include<string.h>
using namespace std;

int n,m;
int a[100],c[100]; //对应原数组和树状数组

int lowbit(int x){
   
   //求sum的时候用到
    return x&(-x);
}

void updata(int i,int k){
   
       //在i位置加上k
    while(i <= n){
   
   
        c[i] += k;
        i += lowbit(i);//更新i以后的前缀和
    }
}

int getsum(int i){
   
           //求A[1 - i]的和
    int res = 0;
    while(i > 0){
   
   
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

int main()
{
   
   
    memset(a, 0, sizeof a);
    memset(c, 0, sizeof c);//全部初始化为0
    cin>>n;
    //创建树状数组
    for(int i = 1; i <= n; i++){
   
   
        cin>>a[i]