不等概抽样
提高估计精度、放回的PPS抽样简化方差计算
前提条件:通常需要一个辅助变量用以确定其入样概率
放回不等概抽样
入样概率的确定:总体的第i个单元被抽中的概率
M
0
M_0
M0:总体的总规模
M
i
M_i
Mi:总体的第i个单元的大小为
M
i
M_i
Mi

这种不等概抽样称作放回的与规模大小成比例的概率抽样简称PPS抽样
PPS的实施主要有两种方法:
代码法
就是根据样本规模来分配代码(id),然后对所有代码进行简单随机抽样
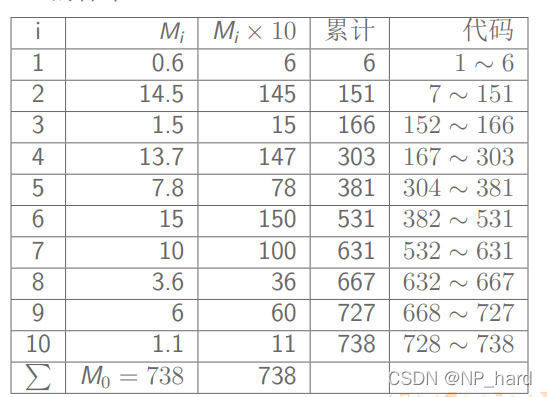
拉希里法
不用累计代码确定样本总数,直接两次随机数决定抽中的单位
第一次:[1, N]之间的随机数i
第二次:[1, max(M)]之间的随机数m
如果
M
i
>
m
M_i > m
Mi>m,则第i个单位被抽中
(只抽取一个样本单元的不等概抽样)
总体总量的估计
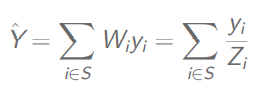

总体总量的方差
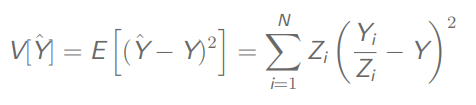
估计量
总体总值
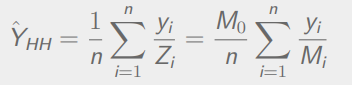
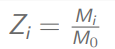
总体总值方差
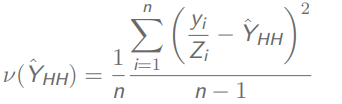
如果采用pps抽样
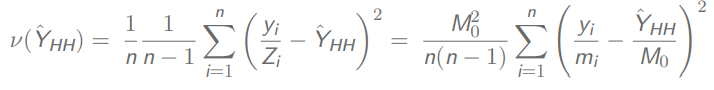
例题

解:
先嗯算一波总体总值
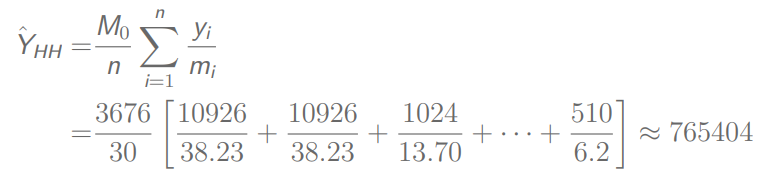
暴算方差和标准差
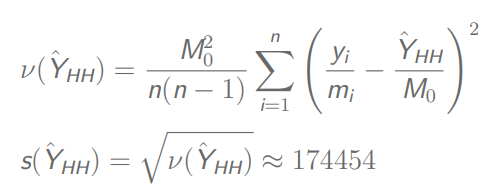
根据置信度得到分位数,然后算相对误差
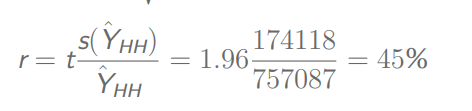
再由公式求出相对误差为20%时的样本量

有放回不等概整群抽样
总体总值(PPS抽样):
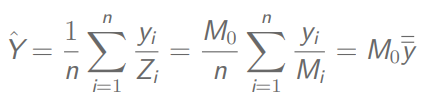
总体方差:
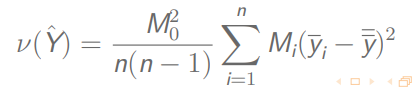
两阶段有放回不等概抽样
总体总值:
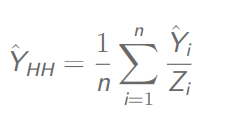
总体方差:
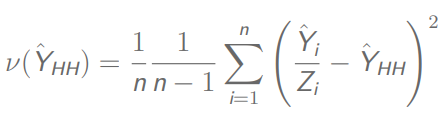
总体总值:
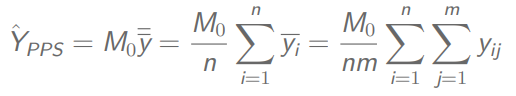
总体方差:
(这里的Y少了个V())
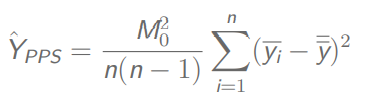
多阶段有放回不等概抽样
总体总值:
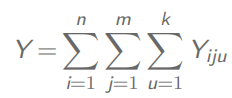
总体方差:
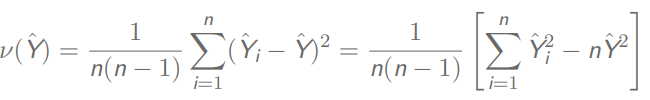
自加权
总体总值:
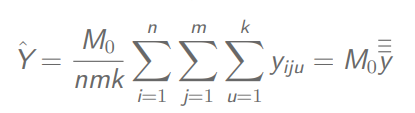
总体方差:
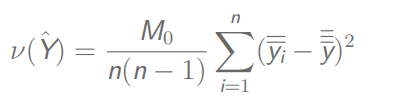
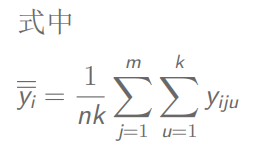
例题
不放回不等概抽样
包含概率:
在不放回不等概抽样中,每个单元的入样概率为
π
i
\pi_i
πi,任意两个单元同时入样的概率为
π
i
j
\pi_{ij}
πij,它们统称为包含概率
对于固定的n,包含概率有:
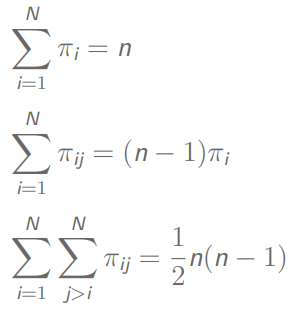
π P S \pi PS πPS抽样

总体总值:
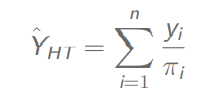
总值方差:
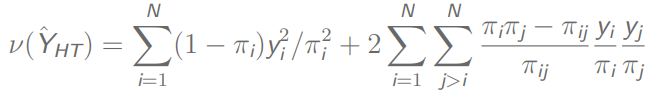
固定n的话,方差为:
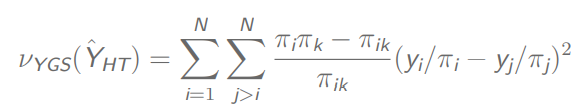
不同情况下的
π
P
S
\pi PS
πPS抽样
👴不玩了,赌一把,肯定不考,内容死鬼多
两阶段不放回不等概抽样
总体总值:
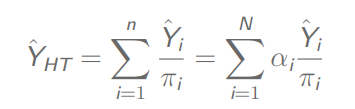
总体方差:
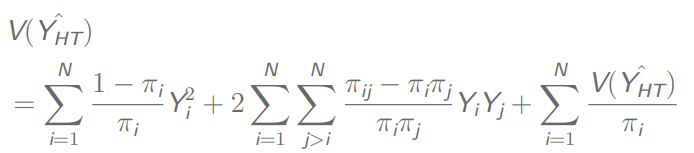





 本文介绍了不等概率抽样技术,重点讨论了放回不等概抽样和不放回不等概抽样的各种形式,包括PPS抽样、整群抽样和两阶段抽样。内容涵盖了抽样概率的确定、估计量的计算以及总体总量和方差的估计,旨在提高估计精度。辅助变量在确定入样概率中的作用和不同抽样方法的适用场景也有所阐述。
本文介绍了不等概率抽样技术,重点讨论了放回不等概抽样和不放回不等概抽样的各种形式,包括PPS抽样、整群抽样和两阶段抽样。内容涵盖了抽样概率的确定、估计量的计算以及总体总量和方差的估计,旨在提高估计精度。辅助变量在确定入样概率中的作用和不同抽样方法的适用场景也有所阐述。
















 1842
1842

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








