C语言中求最大公约数的两种方法：辗转相除法和更相减损术

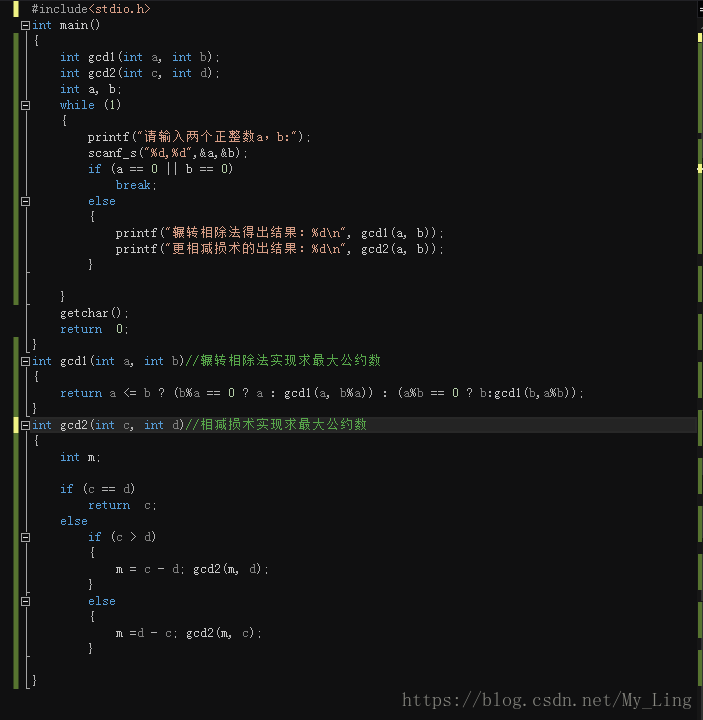
辗转相除法：

       辗转相除法， 又名欧几里德算法（Euclidean algorithm），是求最大公约数的一种方法。它的具体做法是：用较小数除较大数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止。如果是求两个数的最大公约数，那么最后的除数就是这两个数的最大公约数。

更相减损术：

       以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。其中所说的“减数和差数相等的数”，就是 最大公约数。求“等数”的办法是“更相减损”法。

代码部分：

     

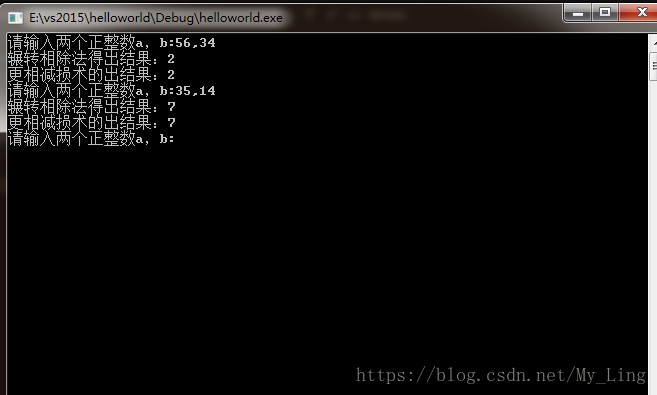
效果图：