Algorithm and Data Structure - leetcode-最小路径和

最新推荐文章于 2026-01-05 22:36:07 发布

原创最新推荐文章于 2026-01-05 22:36:07 发布 · 453 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #动态规划

算法与数据结构专栏收录该内容

1 篇文章

订阅专栏

本文介绍了一种解决LeetCode中“最小路径和”问题的方法，通过动态规划算法实现，并对比了不同初始化列表的方式对代码效率的影响。文章还强调了理解状态转移方程的重要性。

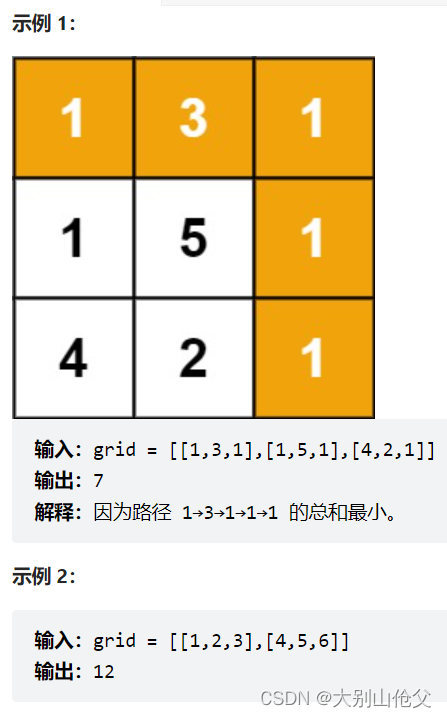
https://leetcode.cn/problems/minimum-path-sum/submissions/
在这里插入图片描述

Tips

使用列表生成式时代码用时更少，但是不熟练的话不建议使用。
dp = [[0]*columns for _ in range(rows)]
直接使用copy（）方法用时长，而且列表的初始值不为0。
dp = grid.copy()
也可以将代码空间复杂度直接变为O(1)，在grid上直接修改。
此题为dynamic programming的二维形式的题，与一维度相比，需要考虑好边界条件以及使用两个for循环，其本质与1D相同。
了解状态-状态转移方程-最优子结构-重叠子问题，较为熟练后尽量牺牲空间来避免递归（Tabulation and Memorization）。

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        if not grid[0]: return 0
        rows, columns = len(grid), len(grid[0])
		# 使用列表生成式时代码用时更少，但是不熟练的话不建议使用
        # dp = [[0]*columns for _ in range(rows)] 
        # 直接使用copy（）方法用时长，而且列表的初始值不为0
        dp = grid.copy()
        for i in range(rows):
            for j in range(columns):
                if i==0 and j==0: 
                    dp[i][j] = grid[i][j]  
                elif j==0:
                    dp[i][j] = grid[i][j] + dp[i-1][j]
                elif i==0:
                    dp[i][j] = grid[i][j] + dp[i][j-1]
                else:
                    dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
        return dp[rows-1][columns-1]