【算法修炼】前缀和

前缀和，和双指针一样，前缀和更多是一种处理技巧，它可以帮助我们 很快地计算出一个连续区间内的和。 通常题目中不会单独为前缀和出题，会隐藏在题目中，需要发掘。

一、区域和检索（简单）

以本题为例讲解如何构造前缀和。

不了解前缀和，可能会写出下面的代码：

class NumArray {
    int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    public int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(left,right);
 */

这并不是最优的，定义一个数组preNum[i]，它记录第0个元素到第 i - 1个元素的和。

// 计算 nums 的累加和
for (int i = 1; i < preSum.length; i++) {
    preSum[i] = preSum[i - 1] + nums[i - 1];
}

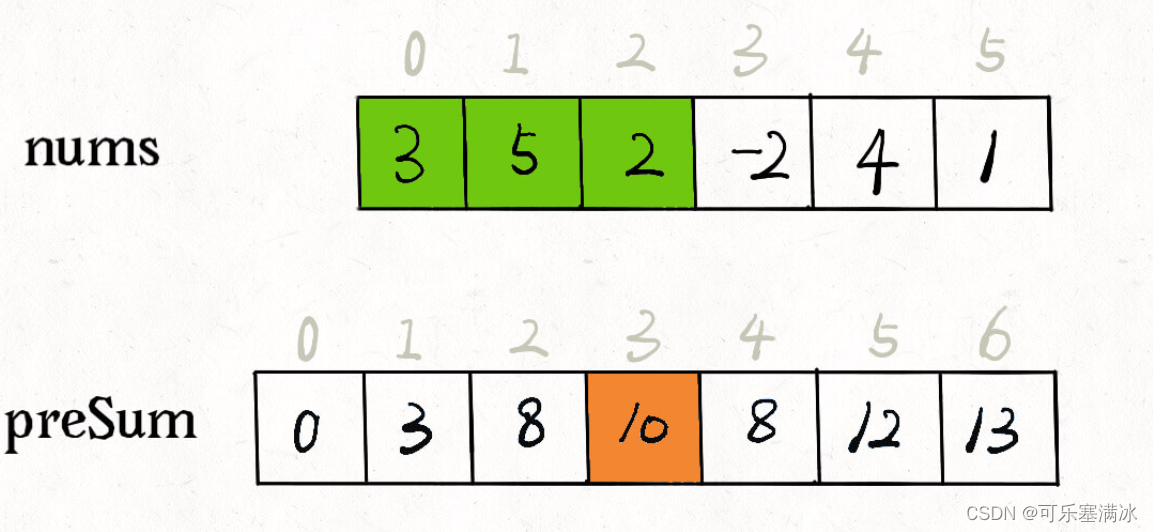
图源：https://labuladong.gitee.io/algo/2/21/56/

有了上图，如果我们要找0 - 1区间的和，就 = presum[2] - presum[0]，找1 - 2区间的和，就 = presum[3] - presum[1]，要注意preSum前缀和数组，是从1开始存的，第0个位置要留给0，这样对于从0下标到任意下标的和才能求得。i - j区间和 = presum[j + 1] - presum[i]，当然也可以不把第一个位置留0，细节要做微调。

下面是经过优化的代码：

class NumArray {
    int[] presum;
    public NumArray(int[] nums) {
        presum = new int[nums.length + 1];
        for (int i = 1; i < nums.length + 1; i++) {
            presum[i] = presum[i - 1] + nums[i - 1]; 
        }
    }
    
    public int sumRange(int left, int right) {
        return presum[right + 1] - presum[left];
    }
}

二、和为k的子数组（中等）

先记录下前缀和数组，遍历所有可能连续子数组，判断和是否=k。

class Solution {
    public int subarraySum(int[] nums, int k) {
        // 先声明前缀和数组
        int[] preSum = new int[nums.length + 1];
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
        // 遍历所有连续子数组，看=k的个数
        int ans = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j <= i; j++) {
                if (preSum[i + 1] - preSum[j] == k) {
                    ans++;
                }
            }
        }
        return ans;
    }
}

但是上面代码的时间复杂度仍然是O(n^2)，还可以如何进行优化呢？

我们可以确定preSum[i]，再去找preSum[i] - k是否存在？存在几个？具体可以用Map实现。

class Solution {
    public int subarraySum(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        int sum = 0;
        int ans = 0;
        // 注意：如果sum - k = 0，答案应该是 + 1
        map.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            // 这个sum就相当于在记录前缀和，就不要数组了
            sum += nums[i];
            if (map.containsKey(sum - k)) {
                ans += map.get(sum - k);
            }
            // 把求得的前缀和放入map
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }
        return ans;
    }
}

这样就可以把时间复杂度降到O(n)。

可以用preSum数组来记录前缀和，也可以通过map来检索前缀和出现的次数，具体选哪种根据题目的意思定。