1.2 Kruskal’s MST Algorithm

最新推荐文章于 2024-05-20 22:00:16 发布

原创最新推荐文章于 2024-05-20 22:00:16 发布 · 282 阅读

0 ·

CC 4.0 BY-SA版权

本文详细解析了Kruskal算法，一种用于寻找加权图最小生成树的有效算法。通过逐步介绍算法原理，包括如何初始化结果、创建顶点集合、排序边并避免闭环，帮助读者理解算法的具体实现过程。

Kruskal’s MST

1. 问题

假设G＝(V, E)是一个无向连通图，U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中u∈U，v∈V－U，则必存在一棵包含边(u,v)的最小生成树。

2. 解析

1、设图的顶点集合为U，树的顶点集合为V
2、从图中任一点出发，选择权重值最小的边，检查加入这条边后最小生成树是否形成闭环，如果没有形成了闭环，加上这条边，否则，跳过这条边。
3、重复步骤2找到V-1条边（x，y），x∈U， y∈V，且权值最小。
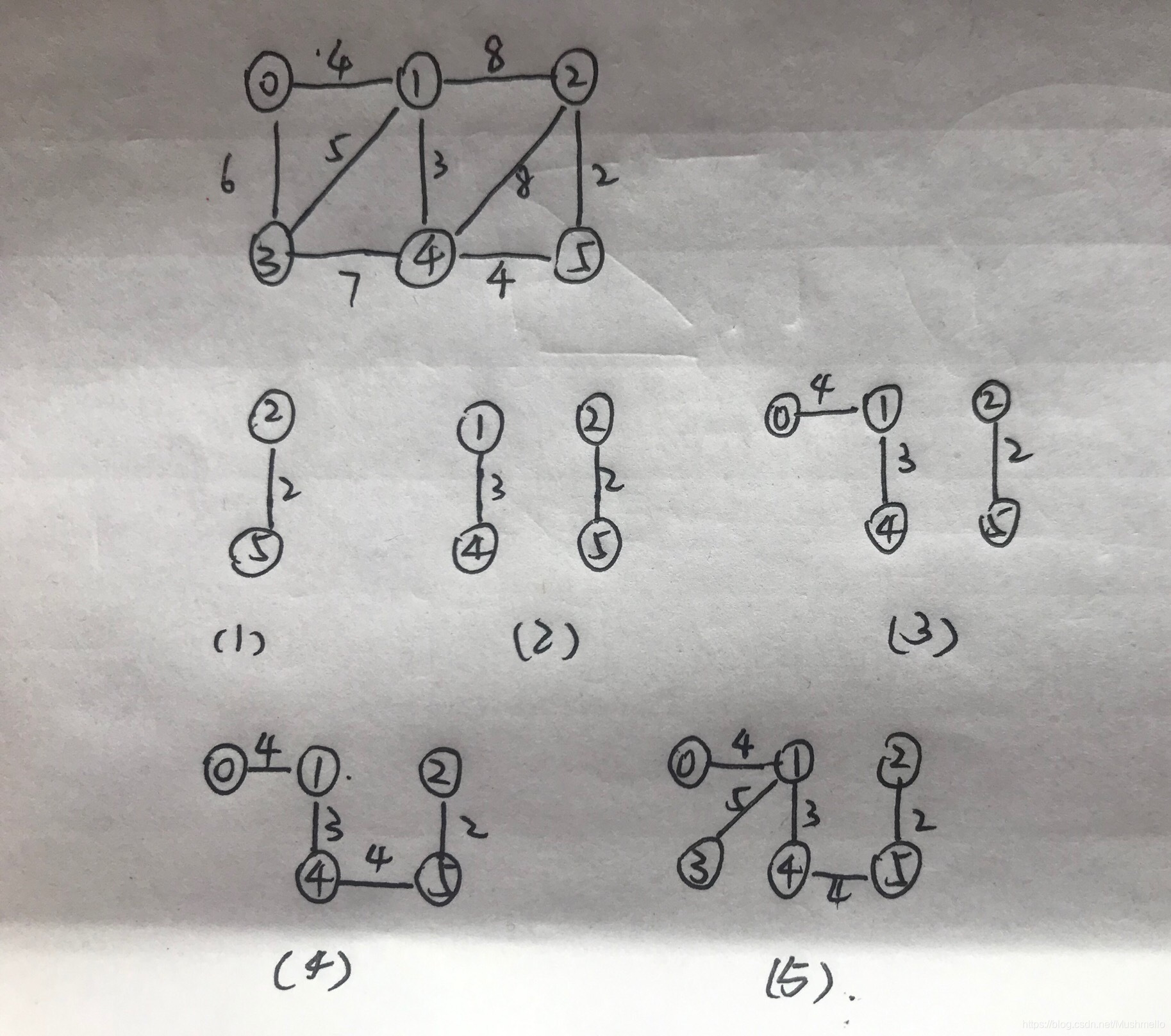
在这里插入图片描述

3. 设计

// Initialize result
mst_weight = 0

// Create V single item sets
for each vertex v
	parent[v] = v;
	rank[v] = 0;

Sort all edges into non decreasing 
order by weight w

for each (u, v) taken from the sorted list  E
    do if FIND-SET(u) != FIND-SET(v)
        print edge(u, v)
        mst_weight += weight of edge(u, v)
        UNION(u, v)