矩形覆盖

贝勒里恩

于 2020-03-25 16:19:37 发布

阅读量185

点赞数

CC 4.0 BY-SA版权

分类专栏： # 刷题记录

本文链接：https://blog.youkuaiyun.com/Mr_robot_strange/article/details/105097960

刷题记录专栏收录该内容

16 篇文章

订阅专栏

本文探讨了一个数学问题，即使用2*1的小矩形无重叠覆盖2*n的大矩形的方法总数，并通过观察规律发现其与斐波那契数列的关系，提供了一种递归解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

比如n=3时，2*3的矩形块有3种覆盖方法：
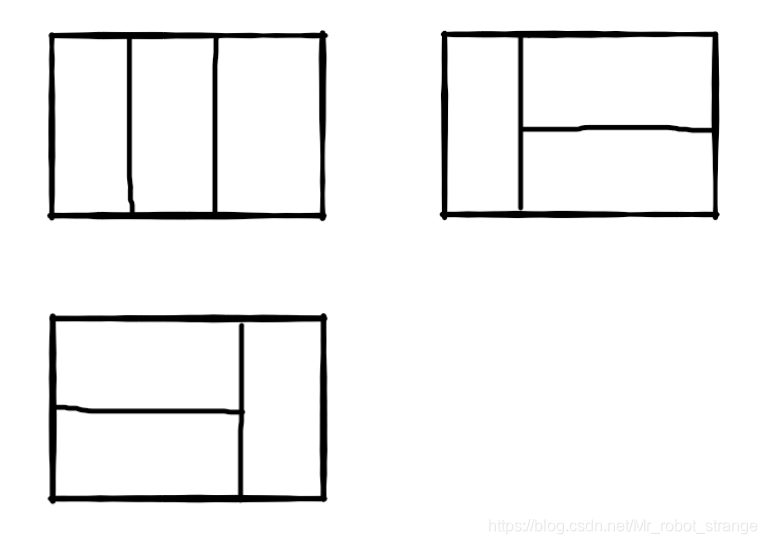
在这里插入图片描述

题目分析：对于这种题型我们可以采取找规律的方法来解答，显然F(0)=0,F(1)=1,F(2)=2,F(3)=3，那么F(4)=?我们可以试着画一下：
在这里插入图片描述
显然只有以上5种覆盖方案，所以F(4)=5，我们已经可以观测到规律了，没错，又是斐波那契数列，所以我们可以推出F(5)=8，小伙伴们可以去画一下验证。
具体代码：

class Solution {
public:
    int rectCover(int number) {
        if(number <= 2)
            return number;
        else
            return rectCover(number-1)+rectCover(number-2);
    }
};