pytorch——实现自编码器和变分自编码器

最新推荐文章于 2025-04-08 18:45:00 发布

Mr. Wanderer

最新推荐文章于 2025-04-08 18:45:00 发布

阅读量4.8k

点赞数 1

分类专栏：机器学习

本文链接：https://blog.youkuaiyun.com/Mr_Wanderer/article/details/119788639

版权

机器学习专栏收录该内容

13 篇文章

订阅专栏

文章目录

数据降维
pytorch实现

本文只设计简单的介绍和pytorch实现，数学原理部分请移步知乎“不刷知乎”大佬的文章：半小时理解变分自编码器
本文部分观点引自上述知乎文章。

数据降维

降维是减少描述数据的特征数量的过程。可以通过选择（仅保留一些现有特征）或通过提取（基于旧特征组合来生成数量更少的新特征）来进行降维。降维在许多需要低维数据（数据可视化，数据存储，繁重的计算…）的场景中很有用。

主成分分析（PCA）

PCA的想法是构建m个新的独立特征，这些特征是n个旧特征的线性组合，并使得这些新特征所定义的子空间上的数据投影尽可能接近初始数据（就欧几里得距离而言）。换句话说，PCA寻找初始空间的最佳线性子空间（由新特征的正交基定义），以使投影到该子空间上的近似数据的误差尽可能小。

自编码器（AE）

简单来说就是使用神经网络做编码器（Encoder）和解码器（Decoder）。

输入和输出的维度是一致的，保证能够重建
中间有一个neck，可以升维或者降维（常用与降维）

在这里插入图片描述
自编码器的缺点：

缺乏规则性：隐空间中缺乏可解释和可利用的结构
自编码器的高自由度使得可以在没有信息损失的情况下进行编码和解码（尽管隐空间的维数较低）但会导致严重的过拟合，这意味着隐空间的某些点将在解码时给出无意义的内容。

变分自编码器（VAE）

隐空间的规则性可以通过两个主要属性表示：

连续性（continuity，隐空间中的两个相邻点解码后不应呈现两个完全不同的内容）；
完整性（completeness，针对给定的分布，从隐空间采样的点在解码后应提供“有意义”的内容）。

简单来说，为了保证隐空间的规则性，VAE的编码器不是将输入编码为隐空间中的单个点，而是将其编码为隐空间中的概率分布。然后解码时按照此概率分布从隐空间中采样进行解码。训练过程：

首先，将输入编码为在隐空间上的分布；
第二，从该分布中采样隐空间中的一个点；
第三，对采样点进行解码并计算出重建误差；
最后，重建误差通过网络反向传播。

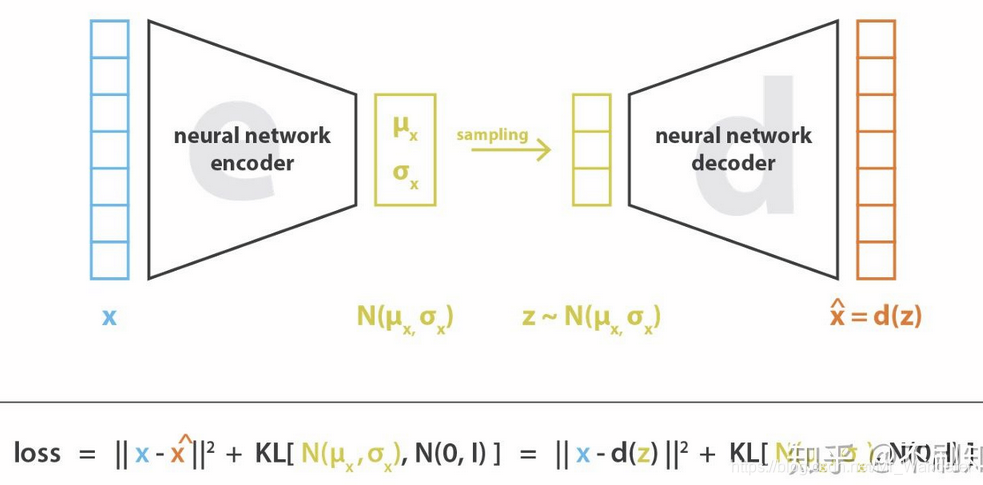在这里插入图片描述

在这里插入图片描述如何计算KL散度：

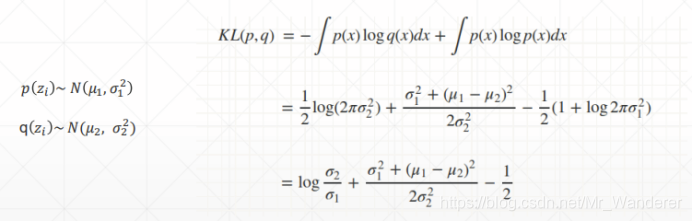
将输入编码为具有一定方差而不是单个点的分布的原因是这样可以非常自然地表达隐空间规则化：编码器返回的分布被强制接近标准正态分布。

pytorch实现

本节实现AE和VAE对MNIST数据集的编码与解码（重现）。

AE

实现自编码器网络结构

'''
定义自编码器网络结构
'''

import torch
from torch import nn


class AE(nn.Module):
    def __init__(self):
        super(AE, self).__init__()

        # [b, 784] => [b, 20]
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 20),
            nn.ReLU()
        )

        # [b, 20] => [b, 784]
        self.decoder = nn.Sequential(
            nn.Linear(20, 64),
            nn.ReLU(),
            nn.Linear(64, 256),
            nn.ReLU(),
            nn.Linear(256, 784),
            nn.Sigmoid()
        )


    def forward(self, x):
        """
        :param x: [b, 1, 28, 28]
        :return:
        """
        batchsz = x.size(0)
        # flatten（打平）
        x = x.view(batchsz, 784)
        # encoder
        x = self.encoder(x)
        # decoder
        x = self.decoder(x)
        # reshape
        x = x.view(batchsz, 1, 28, 28)

        return x

实现AE对MNIST数据集的处理

'''
此处需要安装并开启visdom
安装：pip install visdom
开启：python -m visdom.server
'''

import torch
from torch.utils.data import DataLoader
from torch import nn, optim
from torchvision import transforms, datasets

from ae import AE

import visdom


def main():
    '''import mnist dataset'''
    mnist_train = datasets.MNIST('mnist', True, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_train = DataLoader(mnist_train, batch_size=32, shuffle=True)

    mnist_test = datasets.MNIST('mnist', False, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_test = DataLoader(mnist_test, batch_size=32, shuffle=True)

    '''show shape of data'''
    x, label_unuse = iter(mnist_train).next()
    print('x:', x.shape)  # torch.Size([32, 1, 28, 28])

    '''定义神经网络相关内容'''
    device = torch.device('cuda')
    model = AE().to(device)
    # model = VAE().to(device)
    criteon = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr=1e-3)
    print(model)

    '''可视化'''
    viz = visdom.Visdom()

    for epoch in range(1000):

        '''train'''
        for batchidx, (x, label_unuse) in enumerate(mnist_train):
            # [b, 1, 28, 28]
            x = x.to(device)

            x_hat = model(x)
            loss = criteon(x_hat, x)

            # backprop
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

        print(epoch, 'loss:', loss.item())

        '''test'''
        x, label_unuse = iter(mnist_test).next()
        x = x.to(device)
        with torch.no_grad():
            x_hat = model(x)

        '''show test result'''
        viz.images(x, nrow=8, win='x', opts=dict(title='x'))
        viz.images(x_hat, nrow=8, win='x_hat', opts=dict(title='x_hat'))


if __name__ == '__main__':
    main()

VAE

实现变分自编码器网络结构

'''
定义变分自编码器网络结构
'''

import torch
from torch import nn


class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        # [b, 784] => [b, 20]
        # u: [b, 10]
        # sigma: [b, 10]
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 20),
            nn.ReLU()
        )

        # [b, 10] => [b, 784]
        self.decoder = nn.Sequential(
            nn.Linear(10, 64),
            nn.ReLU(),
            nn.Linear(64, 256),
            nn.ReLU(),
            nn.Linear(256, 784),
            nn.Sigmoid()
        )

        self.criteon = nn.MSELoss()

    def forward(self, x):
        """

        :param x: [b, 1, 28, 28]
        :return:
        """
        batchsz = x.size(0)
        # flatten
        x = x.view(batchsz, 784)

        # encoder
        # [b, 20], including mean and sigma
        h_ = self.encoder(x)

        # [b, 20] => [b, 10] and [b, 10]
        mu, sigma = h_.chunk(2, dim=1)
        # reparametrize trick, epison~N(0, 1)
        h = mu + sigma * torch.randn_like(sigma)  # 随机抽样

        # decoder
        x_hat = self.decoder(h)

        # reshape
        x_hat = x_hat.view(batchsz, 1, 28, 28)

        kld = 0.5 * torch.sum(
            torch.pow(mu, 2) +
            torch.pow(sigma, 2) -
            torch.log(1e-8 + torch.pow(sigma, 2)) - 1
        ) / (batchsz*28*28)  # 计算与标准正态分布相比的散度

        return x_hat, kld

实现VAE对MNIST数据集的处理

'''
此处需要安装并开启visdom
安装：pip install visdom
开启：python -m visdom.server
'''

import torch
from torch.utils.data import DataLoader
from torch import nn, optim
from torchvision import transforms, datasets

from vae import VAE

import visdom


def main():
    '''import data set'''
    mnist_train = datasets.MNIST('mnist', True, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_train = DataLoader(mnist_train, batch_size=32, shuffle=True)

    mnist_test = datasets.MNIST('mnist', False, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_test = DataLoader(mnist_test, batch_size=32, shuffle=True)

    '''show data shape'''
    x, _ = iter(mnist_train).next()
    print('x:', x.shape)  # torch.Size([32, 1, 28, 28])

    '''def model'''
    device = torch.device('cuda')
    model = VAE().to(device)
    criteon = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr=1e-3)
    print(model)

    viz = visdom.Visdom()

    for epoch in range(1000):
        '''train'''
        for batchidx, (x, _) in enumerate(mnist_train):
            # [b, 1, 28, 28]
            x = x.to(device)

            x_hat, kld = model(x)
            loss = criteon(x_hat, x)

            if kld is not None:
                elbo = - loss - 1.0 * kld
                loss = - elbo

            # backprop
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

        print(epoch, 'loss:', loss.item(), 'kld:', kld.item())

        '''test'''
        x, _ = iter(mnist_test).next()
        x = x.to(device)
        with torch.no_grad():
            x_hat, kld = model(x)

        '''show test result'''
        viz.images(x, nrow=8, win='x', opts=dict(title='x'))
        viz.images(x_hat, nrow=8, win='x_hat', opts=dict(title='x_hat'))


if __name__ == '__main__':
    main()