一、KNN算法原理
K近邻是一种基本的分类和回归方法。原理是根据其k个最近邻的训练实例的类别,通过多数表决的方式进行预测。K近邻不具备显示的学习过程。在预测时只是在训练集中找最接近的K个样本进行预测。所以k近邻关键在于如何快速找到邻近的k个样本。尤其是特征维度大,样本数量众多的时候。kd树是进行快速查找的一种方式。
二、KNN算法三要素
KNN算法的三要素:距离度量方式,K值的选择,分类决策规则。
1)距离度量的方式
可有多种度量方式,一般常用Lp距离。
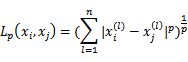
p=2时是欧氏距离,p=1时是曼哈顿距离,p= ∞时,为各维距离最大值。
2)k值选择
k值较小时,模型预测的结果有较小的近似误差,意味着模型越复杂,容易发生过拟合。
k值较大时,模型预测的结果有较大的近似误差,意味着模型越简单。极端例子是K=训练样本总数N。就是训练样本多的那一类就是模型的预测值。
3)分类决策规则
一般是多数表决。
三、KNN算法实现
使用python在不调用sklearn实现KNN算法。代码中skleran只用来生成数据,数据集划分和模型评估。
#%%
import sklearn
from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
X,Y = datasets.make_classification(n_samples=500,n_clusters_per_class=1,n_features=30,n_classes=3)
#%%
#生成数据的形式
print(X.shape)
print(Y.shape)
#%%
x_train,x_test,y_train,y_test = train_test_split(X,Y,test_size=.2)
#%%
'''
k-nn 的三要素:
# 1、k值选择
# 2、距离度量方式
# 3、分类决策规则
k-nn model没有训练的过程,主要要考虑的问题是如何快速对训练数据进行快速的k近邻搜索。
尤其是在特征空间维数大及训练数据容量大时尤其必要
'''
def distance(x1,x2,p):
temp = np.abs(np.array(x1)-np.array(x2))
temp = np.power(temp,p)
temp = np.power(np.sum(temp),1.0/p)
return temp
def k_nn_search(x,x_train,y_train,n=5,p=2):
dis_list = []
for i in range(len(x_train)):
dis_list.append([distance(x,x_train[i],p),y_train[i]])
dis_list.sort(key=lambda x:x[0])
k_res = [i[1] for i in dis_list[0:n]]
counts = np.bincount(k_res)
return np.argmax(counts)
#%%
n = 10
p = 1
preds = []
for j in range(len(x_test)):
pred = k_nn_search(x_test[j],x_train,y_train,n,p)
preds.append(pred)
print(classification_report(y_test,preds))
P=1,N=10时的测试结果如下:
'''
precision recall f1-score support
0 0.89 0.94 0.91 33
1 0.94 0.81 0.87 36
2 0.91 1.00 0.95 31
accuracy 0.91 100
macro avg 0.91 0.91 0.91 100
weighted avg 0.91 0.91 0.91 100
'''










 本文深入讲解了K近邻(KNN)算法的原理,包括其在分类和回归中的应用,探讨了KNN算法的三个核心要素:距离度量方式、K值选择和分类决策规则,并提供了使用Python从零实现KNN算法的示例代码。
本文深入讲解了K近邻(KNN)算法的原理,包括其在分类和回归中的应用,探讨了KNN算法的三个核心要素:距离度量方式、K值选择和分类决策规则,并提供了使用Python从零实现KNN算法的示例代码。
















 958
958

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








