Datawhale Leecode基础算法篇 task03：回溯算法-优快云博客

本文链接：https://blog.youkuaiyun.com/MrBlackmzq/article/details/142456166

官方学习文档：datawhalechina

往期task01：枚举算法链接：Datawhale Leecode基础算法篇 task01：枚举算法

往期task02：递归算法and分治算法：Datawhale Leecode基础算法篇 task02：递归算法and分治算法

回溯算法

回溯算法简介

回溯算法（Backtracking）：一种能避免不必要搜索的穷举式的搜索算法。采用试错的思想，在搜索尝试过程中寻找问题的解，当探索到某一步时，发现原先的选择并不满足求解条件，或者还需要满足更多求解条件时，就退回一步（回溯）重新选择，这种走不通就退回再走的技术称为「回溯法」，而满足回溯条件的某个状态的点称为「回溯点」。

简单来说，回溯算法采用了一种 「走不通就回退」 的算法思想。

回溯算法通常用简单的递归方法来实现，在进行回溯过程中更可能会出现两种情况：

找到一个可能存在的正确答案；
在尝试了所有可能的分布方法之后宣布该问题没有答案。

利用全排列问题理解回溯算法

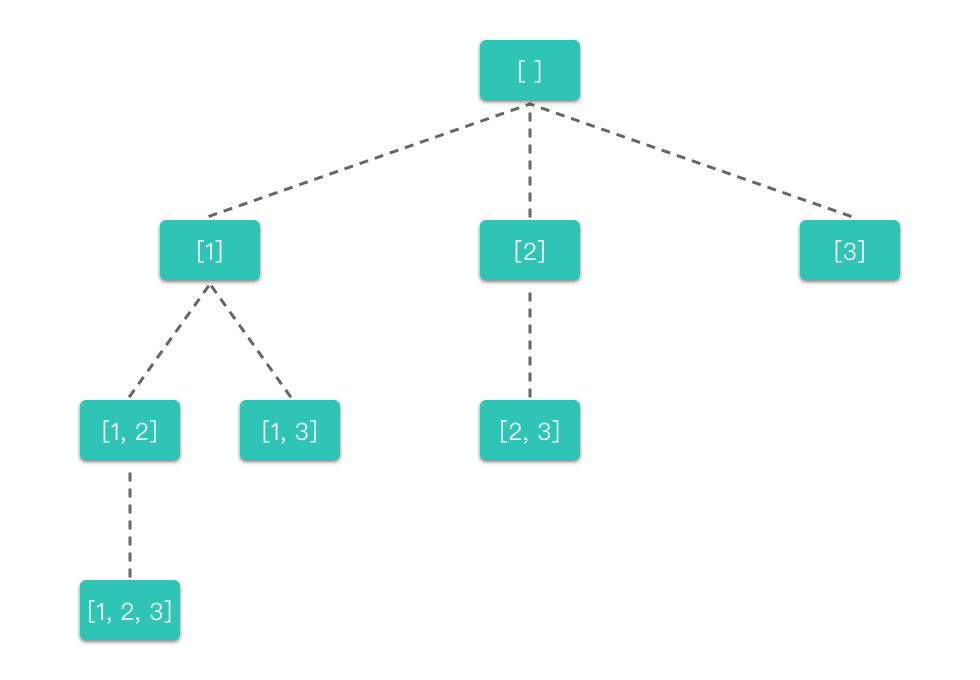
以求解 [1,2,3] 的全排列为例，我们分析一下全排列的回溯过程：

按顺序枚举每一位上可能出现的数字，之前已经出现的数字在接下来要选择的数字中不能再次出现。
对于每一位，进行如下几步：
1. 选择元素：从可选元素列表中选择一个之前没有出现过的元素。
2. 递归搜索：从选择的元素出发，一层层地递归搜索剩下位数，直到遇到边界条件时，不再向下搜索。
3. 撤销选择：一层层地撤销之前选择的元素，转而进行另一个分支的搜索。直到完全遍历完所有可能的路径。

具体决策过程用决策树表示如下图所示：

从中我们可以看出：

每一层中有一个或多个不同的节点，这些节点以及节点所连接的分支代表了「不同的选择」。
每一个节点代表了求解全排列问题的一个「状态」，这些状态是通过「不同的值」来表现的。
每向下递推一层就是在「可选元素列表」中选择一个「元素」加入到「当前状态」。
当一个决策分支探索完成之后，会逐层向上进行回溯。
每向上回溯一层，就是把所选择的「元素」从「当前状态」中移除，回退到没有选择该元素时的状态（或者说重置状态），从而进行其他分支的探索。

根据上文的思路和决策树，我们来写一下全排列的回溯算法代码（假设给定数组 nums 中不存在重复元素）。则代码如下所示：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []    # 存放所有符合条件结果的集合
        path = []   # 存放当前符合条件的结果
        def backtracking(nums):             # nums 为选择元素列表
            if len(path) == len(nums):      # 说明找到了一组符合条件的结果
                res.append(path[:])         # 将当前符合条件的结果放入集合中
                return

            for i in range(len(nums)):      # 枚举可选元素列表
                if nums[i] not in path:     # 从当前路径中没有出现的数字中选择
                    path.append(nums[i])    # 选择元素
                    backtracking(nums)      # 递归搜索
                    path.pop()              # 撤销选择

        backtracking(nums)
        return res

具体对于上述例子，遍历完【1,2】和【1,3】后，那层的backtracking函数就相当于执行结束了，返回上一层进行 path.pop()回到【1】层再返回到【】层，以此类推，实现要求的功能。

回溯算法的通用模板

根据上文全排列的回溯算法代码，我们可以提炼出回溯算法的通用模板，回溯算法的通用模板代码如下所示：

res = []    # 存放所欲符合条件结果的集合
path = []   # 存放当前符合条件的结果
def backtracking(nums):             # nums 为选择元素列表
    if 遇到边界条件:                  # 说明找到了一组符合条件的结果
        res.append(path[:])         # 将当前符合条件的结果放入集合中
        return

    for i in range(len(nums)):      # 枚举可选元素列表
        path.append(nums[i])        # 选择元素
        backtracking(nums)          # 递归搜索
        path.pop()                  # 撤销选择

backtracking(nums)

回溯算法三步走

明确所有选择：画出搜索过程的决策树，根据决策树来确定搜索路径。
明确终止条件：推敲出递归的终止条件，以及递归终止时的要执行的处理方法。
将决策树和终止条件翻译成代码：
1. 定义回溯函数（明确函数意义、传入参数、返回结果等）。
2. 书写回溯函数主体（给出约束条件、选择元素、递归搜索、撤销选择部分）。
3. 明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

回溯算法的终止条件也就是决策树的底层，即达到无法再做选择的条件。

回溯函数的终止条件一般为给定深度、叶子节点、非叶子节点（包括根节点）、所有节点等。并且还要给出在终止条件下的处理方法，比如输出答案，将当前符合条件的结果放入集合中等等。

传入参数和全局变量：是由递归搜索阶段时的「当前状态」来决定的。最好是能通过传入参数和全局变量直接记录「当前状态」。

比如全排列中，backtracking(nums) 这个函数的传入参数是 nums（可选择的元素列表），全局变量是 res（存放所有符合条件结果的集合数组）和 path（存放当前符合条件的结果）。

返回结果：返回结果是在遇到递归终止条件时，需要向上一层函数返回的信息。

一般回溯函数的返回结果都是单个节点或单个数值，告诉上一层函数我们当前的搜索结果是什么即可。

当然，如果使用全局变量来保存「当前状态」的话，也可以不需要向上一层函数返回结果，即返回空结果。比如上文中的全排列。

根据当前可选择的元素列表、给定的约束条件（例如之前已经出现的数字在接下来要选择的数字中不能再次出现）、存放当前状态的变量，就可以写出回溯函数的主体部分。即：
for i in range(len(nums)):          # 枚举可选元素列表
    if 满足约束条件:                  # 约束条件
        path.append(nums[i])        # 选择元素
        backtracking(nums)          # 递归搜索
        path.pop()                  # 撤销选择

回溯算法的应用

子集

题目链接：

78. 子集 - 力扣（LeetCode）

描述：给定一个整数数组 nums，数组中的元素互不相同。

要求：返回该数组所有可能的不重复子集。可以按任意顺序返回解集。

说明：

1≤nums.length≤10。
−10≤nums[i]≤10。
nums 中的所有元素互不相同。

示例：

示例 1：

输入 nums = [1,2,3]
输出 [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

解题思路：

这个问题我们可以用递推解决：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        def generate_subsets(nums):
            if not nums:
                return [[]]
            
            first = nums[0]
            subsets_without_first = generate_subsets(nums[1:])
            subsets_with_first = [[first] + subset for subset in subsets_without_first]
            
            return subsets_without_first + subsets_with_first
        
        return generate_subsets(nums)

递归逻辑：

获取第一个元素 first。
递归调用 generate_subsets(nums[1:]) 来计算不包含第一个元素的所有子集。
对于每个不包含第一个元素的子集，添加 first 来生成包含第一个元素的子集。
将包含和不包含第一个元素的子集合并。

现在我们尝试用本节所学的回溯算法解决：

数组的每个元素都有两个选择：选与不选。

我们可以通过向当前子集数组中添加可选元素来表示选择该元素。也可以在当前递归结束之后，将之前添加的元素从当前子集数组中移除（也就是回溯）来表示不选择该元素。

下面我们根据回溯算法三步走，写出对应的回溯算法。

明确所有选择：根据数组中每个位置上的元素选与不选两种选择，画出决策树，如下图所示。

明确终止条件：

当遍历到决策树的叶子节点时，就终止了。即当前路径搜索到末尾时，递归终止。

那么怎么判断是否到了叶子节点呢？

将决策树和终止条件翻译成代码：

for i in range(index, len(nums)):   # 枚举可选元素列表
    path.append(nums[i])            # 选择元素
    backtracking(nums, i + 1)       # 递归搜索
    path.pop()                      # 撤销选择

定义回溯函数：
- backtracking(nums, index): 函数的传入参数是 nums（可选数组列表）和 index（代表当前正在考虑元素是 nums[i] ），全局变量是 res（存放所有符合条件结果的集合数组）和 path（存放当前符合条件的结果）。
- backtracking(nums, index): 函数代表的含义是：在选择 nums[index] 的情况下，递归选择剩下的元素。
书写回溯函数主体（给出选择元素、递归搜索、撤销选择部分）。
- 从当前正在考虑元素，到数组结束为止，枚举出所有可选的元素。对于每一个可选元素：
  - 约束条件：之前选过的元素不再重复选用。每次从 index 位置开始遍历而不是从 0 位置开始遍历就是为了避免重复。集合跟全排列不一样，子集中 1,2 和 2,1 是等价的。为了避免重复，我们之前考虑过的元素，就不再重复考虑了。
  - 选择元素：将其添加到当前子集数组 path 中。
  - 递归搜索：在选择该元素的情况下，继续递归考虑下一个位置上的元素。
  - 撤销选择：将该元素从当前子集数组 path 中移除。
明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。
- 当遍历到决策树的叶子节点时，就终止了。也就是当正在考虑的元素位置到达数组末尾（即 start≥len(nums)）时，递归停止。
- 从决策树中也可以看出，子集需要存储的答案集合应该包含决策树上所有的节点，应该需要保存递归搜索的所有状态。所以无论是否达到终止条件，我们都应该将当前符合条件的结果放入到集合中。

整体的代码为：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []  # 存放所有符合条件结果的集合
        path = []  # 存放当前符合条件的结果
        def backtracking(nums, index):          # 正在考虑可选元素列表中第 index 个元素
            res.append(path[:])                 # 将当前符合条件的结果放入集合中
            if index >= len(nums):              # 遇到终止条件（本题）
                return

            for i in range(index, len(nums)):   # 枚举可选元素列表
                path.append(nums[i])            # 选择元素
                backtracking(nums, i + 1)       # 递归搜索
                path.pop()                      # 撤销选择

        backtracking(nums, 0)
        return res

也可以简化成这样：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []  # 存放所有符合条件结果的集合
        path = []  # 存放当前符合条件的结果
        
        def backtracking(start_index):
            res.append(path[:])  # 将当前符合条件的结果放入集合中
            
            # 从 start_index 开始枚举可选元素列表
            for i in range(start_index, len(nums)):
                path.append(nums[i])  # 选择元素
                backtracking(i + 1)  # 递归搜索
                path.pop()  # 撤销选择
        
        backtracking(0)
        return res

这里没有显式地在递归函数中使用 return 语句，但是这并不影响它的正常运行。这是因为 Python 的函数如果在函数体中没有显式地使用 return 语句会默认返回 None。

在递归调用的过程中，当递归到达叶子节点，start_index 大于或等于 len(nums) 时，for 循环不会执行，递归自然终止。即使没有显式的 return 语句，递归也会逐层返回，最终返回到最初的调用位置，并返回结果。这是因为递归调用的每一层都在等待其子调用完成并返回控制权。

N 皇后

题目链接：

51. N 皇后 - 力扣（LeetCode）

描述：给定一个整数 n。

要求：返回所有不同的「n 皇后问题」的解决方案。每一种解法包含一个不同的「$n$ 皇后问题」的棋子放置方案，该方案中的 Q 和 . 分别代表了皇后和空位。

说明：

n 皇后问题：将 n 个皇后放置在 n×n 的棋盘上，并且使得皇后彼此之间不能攻击。
皇后彼此不能相互攻击：指的是任何两个皇后都不能处于同一条横线、纵线或者斜线上。
1≤n≤9。

示例：

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如下图所示，4 皇后问题存在 2 个不同的解法。

解题思路：

这道题是经典的回溯问题。我们可以按照行序来放置皇后，也就是先放第一行，再放第二行 …… 一直放到最后一行。

对于 n×n 的棋盘来说，每一行有 n 列，也就有 n 种放法可供选择。我们可以尝试选择其中一列，查看是否与之前放置的皇后有冲突，如果没有冲突，则继续在下一行放置皇后。依次类推，直到放置完所有皇后，并且都不发生冲突时，就得到了一个合理的解。

并且在放置完之后，通过回溯的方式尝试其他可能的分支。

下面我们根据回溯算法三步走，写出对应的回溯算法。

明确所有选择：根据棋盘中当前行的所有列位置上是否选择放置皇后，画出决策树，如下图所示。

明确终止条件：当遍历到决策树的叶子节点时，就终止了。也就是在最后一行放置完皇后时，递归终止。

将决策树和终止条件翻译成代码：

1. 定义回溯函数：

首先我们先使用一个 n∗n 大小的二维矩阵 chessboard 来表示当前棋盘，chessboard 中的字符 Q 代表皇后，. 代表空位，初始都为 .。
然后定义回溯函数 backtrack(chessboard, row): 函数的传入参数是 chessboard（棋盘数组）和 row（代表当前正在考虑放置第 row 行皇后），全局变量是 res（存放所有符合条件结果的集合数组）。
backtrack(chessboard, row): 函数代表的含义是：在放置好第 row 行皇后的情况下，递归放置剩下行的皇后。

2. 书写回溯函数主体（给出选择元素、递归搜索、撤销选择部分）。

枚举出当前行所有的列。对于每一列位置：
- 约束条件：定义一个判断方法，先判断一下当前位置是否与之前棋盘上放置的皇后发生冲突，如果不发生冲突则继续放置，否则则继续向后遍历判断。
- 选择元素：选择 row,col 位置放置皇后，将其棋盘对应位置设置为 Q。
- 递归搜索：在该位置放置皇后的情况下，继续递归考虑下一行。
- 撤销选择：将棋盘上 row,col 位置设置为 . 。

# 判断当前位置 row, col 是否与之前放置的皇后发生冲突
def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):
    for i in range(row):
        if chessboard[i][col] == 'Q':
            return False

    i, j = row - 1, col - 1
    while i >= 0 and j >= 0:
        if chessboard[i][j] == 'Q':
            return False
        i -= 1
        j -= 1
    i, j = row - 1, col + 1
    while i >= 0 and j < n:
        if chessboard[i][j] == 'Q':
            return False
        i -= 1
        j += 1

    return True

这段函数用于判断当前位置是否与之前棋盘上放置的皇后发生冲突，分别表示如果上面的皇后出现在同一列或者左斜线或者右斜线时返回False，否则返回Ture。

for col in range(n):                            # 枚举可放置皇后的列
   if self.isValid(n, row, col, chessboard):   # 如果该位置与之前放置的皇后不发生冲突
       chessboard[row][col] = 'Q'              # 选择 row, col 位置放置皇后
       backtrack(row + 1, chessboard)          # 递归放置 row + 1 行之后的皇后
       chessboard[row][col] = '.'              # 撤销选择 row, col 位置

3. 明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

当遍历到决策树的叶子节点时，就终止了。也就是在最后一行放置完皇后（即 row==n）时，递归停止。
递归停止时，将当前符合条件的棋盘转换为答案需要的形式，然后将其存入答案数组 res 中即可。

代码：

class Solution:
    res = []
    def backtrack(self, n: int, row: int, chessboard: List[List[str]]):
        if row == n:
            temp_res = []
            for temp in chessboard:
                temp_str = ''.join(temp)
                temp_res.append(temp_str)
            self.res.append(temp_res)
            return
        for col in range(n):
            if self.isValid(n, row, col, chessboard):
                chessboard[row][col] = 'Q'
                self.backtrack(n, row + 1, chessboard)
                chessboard[row][col] = '.'

    def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):
        for i in range(row):
            if chessboard[i][col] == 'Q':
                return False

        i, j = row - 1, col - 1
        while i >= 0 and j >= 0:
            if chessboard[i][j] == 'Q':
                return False
            i -= 1
            j -= 1
        i, j = row - 1, col + 1
        while i >= 0 and j < n:
            if chessboard[i][j] == 'Q':
                return False
            i -= 1
            j += 1

        return True

    def solveNQueens(self, n: int) -> List[List[str]]:
        self.res.clear()
        chessboard = [['.' for _ in range(n)] for _ in range(n)]
        self.backtrack(n, 0, chessboard)
        return self.res

if row == n:
    temp_res = []
    for temp in chessboard:
        temp_str = ''.join(temp)
        temp_res.append(temp_str)
    self.res.append(temp_res)
    return

代码的主体部分在之前基本都提到过，约束条件这部分还需要额外再注意一下：

条件判断：
- if row == n: 当 row 的值等于棋盘的大小 n 时，意味着已经成功放置了一个皇后在每一行。
记录解：
- temp_res = []: 创建一个临时列表 temp_res 来保存当前的解。
- for temp in chessboard: 遍历棋盘的每一行。
- temp_str = ''.join(temp): 将当前行的列表转换成字符串。棋盘上每个位置如果是 'Q' 表示放置了皇后，如果是 '.' 表示没有放置皇后。
- temp_res.append(temp_str): 将当前行的字符串表示形式添加到 temp_res 列表中。
保存解：
- self.res.append(temp_res): 将当前的解 temp_res 保存到结果列表 self.res 中。
递归返回：
- return: 找到一个解后，递归返回，不再继续深入搜索。

    def solveNQueens(self, n: int) -> List[List[str]]:
        self.res.clear()
        chessboard = [['.' for _ in range(n)] for _ in range(n)]
        self.backtrack(n, 0, chessboard)
        return self.res

这里self.res.clear()的作用是在每次调用 solveNQueens 方法之前清空结果列表 self.res。这样做的目的是为了避免将前一次计算的结果遗留到当前的计算中，确保每次调用 solveNQueens 方法时都是从一个干净的状态开始计算。

练习

全排列2

题目链接：

0047. 全排列 II - 力扣

描述：给定一个可包含重复数字的序列 nums。

要求：按任意顺序返回所有不重复的全排列。

说明：

1≤nums.length≤8。
−10≤nums[i]≤10。

示例：

示例 1：

输入：nums = [1,1,2]
输出：[[1,1,2],[1,2,1],[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

解题思路：

这道题跟「0046. 全排列」不一样的地方在于增加了序列中的元素可重复这一条件。这就涉及到了如何去重。我们可以先对数组 nums 进行排序，然后使用一个数组 visited 标记该元素在当前排列中是否被访问过。如果未被访问过则将其加入排列中，并在访问后将该元素变为未访问状态。

然后再递归遍历下一层元素之前，增加一句语句进行判重：

if i > 0 and nums[i] == nums[i - 1] and not visited[i - 1]: continue。

这里前一个相同的元素visited[i - 1]值为False时跳到下一个循环是因为这证明了这时前一个元素已经被访问过了，而不是前一个元素正在被访问的阶段（也就是正在求解包含前一个元素的子集）

然后再进行回溯遍历。

代码：

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        res = []    # 存放所欲符合条件结果的集合
        path = []   # 存放当前符合条件的结果
        visited = [False for _ in range(len(nums))]
        nums.sort()
        def backtracking(nums,visited):             # nums 为选择元素列表
            if len(path) == len(nums):                  # 说明找到了一组符合条件的结果
                res.append(path[:])         # 将当前符合条件的结果放入集合中
                return

            for i in range(len(nums)):      # 枚举可选元素列表
                if i > 0 and nums[i] == nums[i - 1] and not visited[i - 1] :
                    continue
                if  not visited[i]:
                    visited[i]=True
                    path.append(nums[i])        # 选择元素
                    backtracking(nums,visited)          # 递归搜索
                    path.pop()                  # 撤销选择
                    visited[i]=False
        
        visited = [False for _ in range(len(nums))]
        backtracking(nums,visited)
        return res

这是基于Leetcode算法笔记以及全排列1的代码按照回溯算法的通用模版修改完善出的代码，与算法笔记不同的是，我将对应的两个函数结合起来了，这里要注意的是，对于这行代码的处理：

if  not visited[i]:

而不能是：

 if nums[i] not in path  and not visited[i]:

这是因为与nums[i]相同的值，比如nums[i-1]也会同样被代码判断在不在path中，这会导致代码把相同的元素筛去而出现错误。

这里是算法笔记的完整代码，可以作为参照：

class Solution:
    res = []
    path = []
    def backtrack(self, nums: List[int], visited: List[bool]):
        if len(self.path) == len(nums):
            self.res.append(self.path[:])
            return
        for i in range(len(nums)):
            if i > 0 and nums[i] == nums[i - 1] and not visited[i - 1]:
                continue

            if not visited[i]:
                visited[i] = True
                self.path.append(nums[i])
                self.backtrack(nums, visited)
                self.path.pop()
                visited[i] = False

    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        self.res.clear()
        self.path.clear()
        nums.sort()
        visited = [False for _ in range(len(nums))]
        self.backtrack(nums, visited)
        return self.res

子集2

题目链接:子集2

描述：给定一个整数数组 nums，其中可能包含重复元素。

要求：返回该数组所有可能的子集（幂集）。

说明：

解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。
1≤nums.length≤10。
−10≤nums[i]≤10。

示例：

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

实现思路：

在原求解子集1的代码基础上修改即可，原代码为：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []  # 存放所有符合条件结果的集合
        path = []  # 存放当前符合条件的结果
        def backtracking(nums, index):          # 正在考虑可选元素列表中第 index 个元素
            res.append(path[:])                 # 将当前符合条件的结果放入集合中
            if index >= len(nums):              # 遇到终止条件（本题）
                return

            for i in range(index, len(nums)):   # 枚举可选元素列表
                path.append(nums[i])            # 选择元素
                backtracking(nums, i + 1)       # 递归搜索
                path.pop()                      # 撤销选择

        backtracking(nums, 0)
        return res

我们只要考虑对重复元素的处理即可，参考全排列2问题，我们首先需要对sums数组排序，然后在递归搜索前加一个小小的判断即可，如果出现相同元素则跳到下一个循环中去，这里判断i > index是为了防止i为index时出现错误：

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        res = []  # 存放所有符合条件结果的集合
        path = []  # 存放当前符合条件的结果
        nums.sort()
        def backtracking(nums, index):          # 正在考虑可选元素列表中第 index 个元素
            res.append(path[:])                 # 将当前符合条件的结果放入集合中
            if index >= len(nums):              # 遇到终止条件（本题）
                return

            for i in range(index, len(nums)):   # 枚举可选元素列表
                if i > index and nums[i] == nums[i - 1]:
                    continue
                path.append(nums[i])            # 选择元素
                backtracking(nums, i + 1)       # 递归搜索
                path.pop()                      # 撤销选择

        backtracking(nums, 0)
        return res

如此我们就简单的了解了回溯算法，后续的拓展算法练习我会持续更新，那么今天的学习就到这里，我我们下期再见！