Datawhale Leecode基础算法篇 task01：枚举算法-优快云博客

确定枚举对象、枚举范围和判断条件，并判断条件设立的正确性。
1. 确定枚举对象：枚举对象为公鸡、母鸡、小鸡的只数，那么我们可以用变量 x、y、z 分别来代表公鸡、母鸡、小鸡的只数。
2. 确定枚举范围：因为总共买了 100 只鸡，所以 0≤x,y,z≤100，则 x、y、z 的枚举范围为 [0,100]。
3. 确定判断条件：根据题意，我们可以列出两个方程式：5x + 3y + 1/3z = 100，x + y + z = 100。在枚举 x、y、z 的过程中，我们可以根据这两个方程式来判断当前状态是否满足题意。
一一枚举可能的情况，并验证是否是问题的解。
- 根据枚举对象、枚举范围和判断条件，我们可以顺利写出对应的代码。

class Solution:
    def buyChicken(self):
        for x in range(101):
            for y in range(101):
                for z in range(101):
                    if z % 3 == 0 and 5 * x + 3 * y + z // 3 == 100 and x + y + z == 100:
                        print("公鸡 %s 只，母鸡 %s 只，小鸡 %s 只" % (x, y, z))

3.考虑提高枚举算法的效率。

在上面的代码中，我们枚举了 x、y、z，但其实根据方程式 x+y+z=100，得知：z 可以通过 z=100−x−y 而得到，这样我们就不用再枚举 z 了。
在上面的代码中，对 x、y 的枚举范围是 [0,100]，但其实如果所有钱用来买公鸡，最多只能买 20 只，同理，全用来买母鸡，最多只能买 33 只。所以对 x 的枚举范围可改为 [0,20]，y 的枚举范围可改为 [0,33]。

class Solution:
    def buyChicken(self):
        for x in range(21):
            for y in range(34):
                z = 100 - x - y
                if z % 3 == 0 and 5 * x + 3 * y + z // 3 == 100:
                    print("公鸡 %s 只，母鸡 %s 只，小鸡 %s 只" % (x, y, z))

枚举算法的应用

两数之和

题目链接：两数之和 - 力扣

描述：给定一个整数数组 nums 和一个整数目标值 target。

要求：在该数组中找出和为 target 的两个整数，并输出这两个整数的下标。可以按任意顺序返回答案。

说明：

2 ≤nums.length≤ 104。
−109 ≤nums[i]≤ 109。
−109 ≤target≤ 109。
只会存在一个有效答案。

示例：

示例 1：

输入：nums = [2,7,11,15], target = 9

输出：[0,1]

解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6

输出：[1,2]

解题思路

这里说下枚举算法的解题思路。

使用两重循环枚举数组中每一个数 nums[i]、nums[j]，判断所有的 nums[i]+nums[j] 是否等于 target。
如果出现 nums[i]+nums[j]==target，则说明数组中存在和为 target 的两个整数，将两个整数的下标 i、j 输出即可。

代码

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums)):
            for j in range(i + 1, len(nums)):
                if i != j and nums[i] + nums[j] == target:
                    return [i, j]
        return []

self: 是指向当前对象实例的引用，在类的方法内部不需要显式传递，但在调用时会被自动传入。
nums: List[int]: 表示输入参数是一个整数类型的列表。
target: int: 表示输入参数是一个整数。
-> List[int]: 这是一个类型注解，表示该方法返回一个整数列表（如果遍历完所有的可能组合后仍然没有找到符合条件的两个元素，则返回一个空列表 []）。

复杂度分析

时间复杂度： $O(n^2)$ ，其中 n 为数组 nums 的元素数量。
空间复杂度： $O(1)$ 。（所需内存空间在一个固定的界限内，不会随着输入规模的增长而增长）

计数质数

题目链接：计数质数-力扣

描述：给定一个非负整数 n。

要求：统计小于 n 的质数数量。

说明：

0 ≤ n ≤ 5 × $10^{6}$ 。

示例：

示例 1：

输入 n = 10
输出 4
解释 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7。

示例 2：

输入：n = 1
输出：0

解题思路

这里说下枚举算法的解题思路（注意：提交会超时，只是讲解一下枚举算法的思路）。

对于小于 n 的每一个数 x，我们可以枚举区间 [2,x−1] 上的数是否是 x 的因数，即是否存在能被 x 整除的数。如果存在，则该数 x 不是质数。如果不存在，则该数 x 是质数。这样我们就可以通过枚举 [2,n−1] 上的所有数 x，并判断 x 是否为质数。

在遍历枚举的同时，我们定义一个用于统计小于 n 的质数数量的变量 cnt。如果符合要求，则将计数 cnt 加 1。最终返回该数目作为答案。

考虑到如果 i 是 x 的因数，则 x/i 也必然是 x 的因数，则我们只需要检验这两个因数中的较小数即可。而较小数一定会落在 $[2,\sqrt{x}]$ 上。因此我们在检验 x 是否为质数时，只需要枚举 $[2,\sqrt{x}]$ 中的所有数即可。

利用枚举算法单次检查单个数的时间复杂度为 $O(\sqrt{n})$ ，检查 n 个数的整体时间复杂度为 $O(n\sqrt{n})$ 。

代码

class Solution:
    def isPrime(self, x):
        for i in range(2, int(pow(x, 0.5)) + 1):
            if x % i == 0:
                return False
        return True

    def countPrimes(self, n: int) -> int:
        cnt = 0
        for x in range(2, n):
            if self.isPrime(x):
                cnt += 1
        return cnt

复杂度分析

时间复杂度： $O(n \times \sqrt{n})$ 。
空间复杂度： $O(1)$ 。

统计平方和三元组的数目

题目链接：统计平方和三元组的数目-力扣

描述：给你一个整数 n。

要求：请你返回满足 1 ≤a,b,c≤ n 的平方和三元组的数目。

说明：

平方和三元组：指的是满足 $a^{2}+b^{2}=c^{2}$ 的整数三元组 (a,b,c)。
1 ≤ n ≤ 250。

示例：

示例 1：

输入 n = 5
输出 2
解释 平方和三元组为 (3,4,5) 和 (4,3,5)。

示例 2：

输入：n = 10
输出：4
解释：平方和三元组为 (3,4,5)，(4,3,5)，(6,8,10) 和 (8,6,10)。

此处表示a、b交换位置的话不是同一组。

解题思路

我们可以在 [1,n] 区间中枚举整数三元组 (a,b,c) 中的 a 和 b。然后判断 $a^{2}+b^{2}$ 是否等于 $c^{2}$ 且c小于等于 n。

在遍历枚举的同时，我们定义一个用于统计平方和三元组数目的变量 cnt。如果符合要求，则将计数 cnt 加 1。最终，我们返回该数目作为答案。

利用枚举算法统计平方和三元组数目的时间复杂度为 $O(n^{2})$ 。

注意：在计算中，为了防止浮点数造成的误差，并且两个相邻的完全平方正数之间的距离一定大于 1，所以我们可以用 $\sqrt{a^{2}+b^{2}+1}$ 来代替 $\sqrt{a^{2}+b^{2}}$ 。

代码

class Solution:
    def countTriples(self, n: int) -> int:
        cnt = 0
        for a in range(1, n + 1):
            for b in range(1, n + 1):
                c = int(sqrt(a * a + b * b + 1))
                if c <= n and a * a + b * b == c * c:
                    cnt += 1
        return cnt

复杂度分析

时间复杂度： $O(n^2)$ 。
空间复杂度： $O(1)$ 。

练习

练习一的题目上面都讲过

公因子的数目

题目链接：https://leetcode.cn/problems/number-of-common-factors/

描述：给定两个正整数 a 和 b。

要求：返回 a 和 b 的公因子数目。

说明：

公因子：如果 x 可以同时整除 a 和 b，则认为 x 是 a 和 b 的一个公因子。
1≤a,b≤1000。

示例：

示例 1：

输入：a = 12, b = 6
输出：4
解释：12 和 6 的公因子是 1、2、3、6。

示例 2：

输入：a = 25, b = 30
输出：2
解释：25 和 30 的公因子是 1、5。

代码：

class Solution:
    def commonFactors(self, a: int, b: int) -> int:
        cnt=0
        for i in range(1,int(min(a,b)+1)):
            if a % i ==0 and b % i==0:
                cnt+=1
        return cnt

因为a、b两者的最大公因子一定小于等于两者的较小值，因此可据此对 i 的约束条件进行简化。

和为s的正数序列

题目链接：https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/

描述：给定一个正整数 target。

要求：输出所有和为 target 的连续正整数序列（至少含有两个数）。序列中的数字由小到大排列，不同序列按照首个数字从小到大排列。

说明：

1≤target≤105。

示例：

示例 1：

输入：target = 9
输出：[[2,3,4],[4,5]]

示例 2：

输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

代码：

class Solution:
    def fileCombination(self, target: int) -> List[List[int]]:
        you_list = []
        for k in range(2,1000):
            for n in range(int(target//k-k//2)-1,int(target//k-k//2)+2):
                my_list = []
                if k*n + 1/2*k*(k-1)==target:
                    if n<=0:
                        continue
                    for i in range(n,n+k):
                        my_list.append(i)
                    you_list.append(my_list)
        you_list.sort(key=lambda x: x[0])
        return you_list

首先要注意返回的是List[List[int]]类型，不同序列按照首个数字从小到大排列表示最后还需要对列表进行排序。

观察发现，如果把满足条件的一组值第一个值设为n，之后就是n+1、n+2……，这组值一共有k个，其和满足f(k)=kn+1/2k(k−1)，由此可以得出判断条件kn+1/2k(k−1)==target。

然后根据已定的k可以推出n的大概范围，即在target/k取中间值后减去k/2附近。

此外注意列表清空 ! 把子列表放在循环内定义，避免重复添加同一个子列表。

return会直接终止函数执行，为了避免找到一组值就输出，我们只在循环中将子列表加入列表，最后在return。

还有注意要输出的是连续正整数序列，要注意约束条件避免输出负值和0。现在这个约束条件应该还有改进的空间，因为现在是先筛选出满足条件的n值在对其进行处理，应该会有方法在筛选的同时就避免了输出负值和0，之后写出来再改进吧。

统计圆内格点数目

描述：给定一个二维整数数组 circles。其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆。

要求：返回出现在至少一个圆内的格点数目。

说明：

格点：指的是整数坐标对应的点。
圆周上的点也被视为出现在圆内的点。
1≤circles.length≤200。
circles[i].length==3。
1≤xi,yi≤100。
1≤ri≤min(xi,yi)。

示例：

示例 1：

输入：circles = [[2,2,1]]
输出：5
解释：
给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。
因此，出现在至少一个圆内的格点数目是 5。

示例 2：

输入：circles = [[2,2,2],[3,4,1]]
输出：16
解释：
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4)。

代码：

class Solution:
    def countLatticePoints(self, circles: List[List[int]]) -> int:
        map_dict = {}
        for (xi, yi, ri) in circles:
            for tmp_x in range(xi - ri, xi + ri + 1):
                for tmp_y in range(yi - ri, yi + ri + 1):
                    if (tmp_x - xi) * (tmp_x - xi) + (tmp_y - yi) * (tmp_y - yi) <= ri * ri:
                        map_dict[(tmp_x, tmp_y)] = 1
        return len(map_dict)

初始化一个空字典 map_dict，用来存储所有被至少一个圆覆盖的格点坐标。键是格点的坐标 (tmp_x, tmp_y)，值为 1，表示该格点已被记录。

如果 (tmp_x, tmp_y) 在圆内，则将其坐标作为键存入 map_dict 中，并赋予值 1。这样可以确保每个格点只被记录一次。

在既定时间做作业的人数

描述：给你两个长度相等的整数数组，一个表示开始时间的数组 startTime ，另一个表示结束时间的数组 endTime。再给定一个整数 queryTime 作为查询时间。已知第 i 名学生在 startTime[i] 时开始写作业并于 endTime[i] 时完成作业。

要求：返回在查询时间 queryTime 时正在做作业的学生人数。即能够使 queryTime 处于区间 [startTime[i],endTime[i]] 的学生人数。

说明：

startTime.length==endTime.length。
1 ≤ startTime.length ≤ 100。
1 ≤ startTime[i] ≤ endTime[i] ≤ 1000。
1 ≤ queryTime ≤ 1000。

示例：

示例 1：

输入：startTime = [4], endTime = [4], queryTime = 4
输出：1
解释：在查询时间只有一名学生在做作业。

代码：

class Solution:
    def busyStudent(self, startTime: List[int], endTime: List[int], queryTime: int) -> int:
        cnt=0
        for i in range(0,len(startTime)):
            if startTime[i]<= queryTime <= endTime[i]:
                cnt+=1
        return cnt

和为K的子数组

题目链接：https://leetcode.cn/problems/subarray-sum-equals-k/

描述：给定一个整数数组 nums 和一个整数 k。

要求：找到该数组中和为 k 的连续子数组的个数。

说明：

1 ≤ nums.length ≤ $2\times 10^{4}$ 。
−1000 ≤ nums[i] ≤ 1000。 $-10^{7}$ ≤ k ≤ $10^{7}$ 。

示例：

示例 1：

输入：nums = [1,1,1], k = 2

输出：2

示例 2：

输入：nums = [1,2,3], k = 3
输出：2

代码：

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        cnt = 0
        
        # 子数组的最大长度
        max_length = len(nums)
        
        # 遍历子数组的长度
        for i in range(1, max_length + 1):
            # 遍历子数组的起始位置
            for start in range(max_length - i + 1):
                sum = 0
                # 计算当前子数组的和
                for j in range(start, start + i):
                    sum += nums[j]
                    
                    
                # 如果当前子数组的和等于 k，则计数器加 1
                if sum == k:
                    cnt += 1
                    
        return cnt

先按照简单思路解决，显然这种方法有三层嵌套循环，时间复杂度高，在面对大量数据时会出现超出时间限制的情况，现在对其进行优化。

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        count = 0
        current_sum = 0
        prefix_sums = {0: 1}
        
        for num in nums:
            current_sum += num
            if current_sum - k in prefix_sums:
                count += prefix_sums[current_sum - k]
            if current_sum in prefix_sums:
                prefix_sums[current_sum] += 1
            else:
                prefix_sums[current_sum] = 1
        
        return count

这种方法通过利用哈希表，找到一个子数组，使得 current_sum - previous_sum = k，即 previous_sum = current_sum - k。换句话说，我们需要找到一个之前遇到过的前缀和，使得当前前缀和减去这个前缀和等于 k。

如果 current_sum - k 已经存在于 prefix_sums 中，那么说明从某个位置到当前位置的子数组的和为 k。此时，我们就可以增加计数器 count。

网络信号最好的坐标

题目链接:https://leetcode.cn/problems/coordinate-with-maximum-network-quality/

给你一个数组 towers 和一个整数 radius 。

数组 towers 中包含一些网络信号塔，其中 towers[i] = [xi, yi, qi] 表示第 i 个网络信号塔的坐标是 (xi, yi) 且信号强度参数为 qi 。所有坐标都是在 X-Y 坐标系内的整数坐标。两个坐标之间的距离用 欧几里得距离 计算。

整数 radius 表示一个塔 能到达 的 最远距离 。如果一个坐标跟塔的距离在 radius 以内，那么该塔的信号可以到达该坐标。在这个范围以外信号会很微弱，所以 radius 以外的距离该塔是 不能到达的 。

如果第 i 个塔能到达 (x, y) ，那么该塔在此处的信号为 ⌊qi / (1 + d)⌋ ，其中 d 是塔跟此坐标的距离。一个坐标的 信号强度 是所有 能到达 该坐标的塔的信号强度之和。

请你返回数组 [cx, cy] ，表示 信号强度 最大的整数坐标点 (cx, cy) 。如果有多个坐标网络信号一样大，请你返回字典序最小的非负坐标。

注意：

坐标 (x1, y1) 字典序比另一个坐标 (x2, y2) 小，需满足以下条件之一：
- 要么 x1 < x2 ，
- 要么 x1 == x2 且 y1 < y2 。
⌊val⌋ 表示小于等于 val 的最大整数（向下取整函数）。

示例 1：

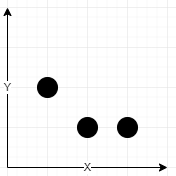
输入：towers = [[1,2,5],[2,1,7],[3,1,9]], radius = 2
输出：[2,1]
解释：
坐标 (2, 1) 信号强度之和为 13
- 塔 (2, 1) 强度参数为 7 ，在该点强度为 ⌊7 / (1 + sqrt(0)⌋ = ⌊7⌋ = 7
- 塔 (1, 2) 强度参数为 5 ，在该点强度为 ⌊5 / (1 + sqrt(2)⌋ = ⌊2.07⌋ = 2
- 塔 (3, 1) 强度参数为 9 ，在该点强度为 ⌊9 / (1 + sqrt(1)⌋ = ⌊4.5⌋ = 4
没有别的坐标有更大的信号强度。

示例 2：

输入：towers = [[23,11,21]], radius = 9
输出：[23,11]
解释：由于仅存在一座信号塔，所以塔的位置信号强度最大。

示例 3：

输入：towers = [[1,2,13],[2,1,7],[0,1,9]], radius = 2
输出：[1,2]
解释：坐标 (1, 2) 的信号强度最大。

提示：

1 <= towers.length <= 50
towers[i].length == 3
0 <= xi, yi, qi <= 50
1 <= radius <= 50

代码：

import math
class Solution:
    def bestCoordinate(self, towers: List[List[int]], radius: int) -> List[int]:
        max=0
        x_max=0
        y_max=0
        for x in range(100):
            for y in range(100):
                sum=0
                for i in range(len(towers)):
                    if math.sqrt((x-towers[i][0])*(x-towers[i][0])+(y-towers[i][1])*(y-towers[i][1]))<= radius:
                        d=math.sqrt((x-towers[i][0])*(x-towers[i][0])+(y-towers[i][1])*(y-towers[i][1]))
                        sum+=int(towers[i][2]//(1+d))
                if sum>max:
                    max=sum
                    x_max=x
                    y_max=y
                if sum==max:
                    if x<x_max or (x==x_max and y<y_max):
                        x_max=x
                        y_max=y
        return [x_max,y_max]

这里采用了最笨的方法暴力求解，效率比较低。

最大正方形

题目链接：https://leetcode.cn/problems/maximal-square/

描述：给定一个由 '0' 和 '1' 组成的二维矩阵 matrix。

要求：找到只包含 '1' 的最大正方形，并返回其面积。

说明：

m==matrix.length。
n==matrix[i].length。
1≤m,n≤300。
matrix[i][j] 为 `'0'` 或 `'1'`。

示例：

示例 1：

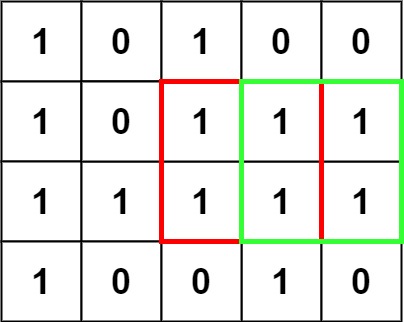
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],
["1","0","0","1","0"]]
输出：4

示例 2：

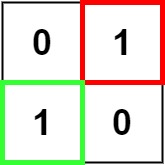
输入：matrix = [["0","1"],["1","0"]]
输出：1

代码:



class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        """
        dp[i][j] 表示以第 i 行第 j 列为右下角所能构成的最大正方形边长，
        则递推式为：
        dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
        """
        m = len(matrix)
        if m == 0:
            return 0
        n = len(matrix[0])
        max_side = 0
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if matrix[i-1][j-1] == '1':
                    dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
                    max_side = max(max_side, dp[i][j])
        
        return max_side * max_side

m 和 n：分别表示矩阵的行数和列数。
max_side：记录最大正方形的边长。
dp：动态规划的二维列表，用于存储每个位置的最大正方形边长。列表的大小为 (m + 1) x (n + 1)，多出的一行一列用于边界条件的处理。

                if matrix[i-1][j-1] == '1':
                    dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
                    max_side = max(max_side, dp[i][j])

条件判断：如果当前位置的元素为 '1'，则考虑能否形成更大的正方形。
递推公式：dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])，表示当前位置 (i, j) 可以形成的最大正方形边长为 1 加上三个相邻位置的最小值。

这里的逻辑是：

如果当前位置 (i, j) 为 '1'，则可以考虑它是否能成为某个正方形的一个角。
如果它可以成为一个正方形的一个角，那么该正方形的边长将是 1 加上三个相邻位置（左上角、上方、左侧）的最大正方形边长的最小值。
例如，如果当前位置 (i, j) 的左上角、上方和左侧的最大正方形边长分别为 a、b 和 c，那么当前位置 (i, j) 的最大正方形边长就是 1 + min(a, b, c)。

这段代码能够正确地找出给定矩阵中最大正方形的边长，并返回该正方形的面积。通过动态规划的方法，代码的时间复杂度为 O(m * n)，空间复杂度为 O(m * n)。

感谢大家的观看，我们下期再见！