从约瑟夫斯问题引发的算法优化_约瑟夫问题python优化-优快云博客

本文链接：https://blog.youkuaiyun.com/MorganFish/article/details/148419783

文章目录

前言

【序】¹
在翻阅《西望》杂志的时候，偶然看到一篇题为对于约瑟夫斯问题的概率条件变种问题的求解与论证（之后简称原文）的文章，详尽地向读者介绍了并综合信息技术与数学方法论证了约瑟夫斯问题（的变种）。然而读的过程中，我们发现这篇八页的报告中，利用Python模拟实验流程并且绘制图表的代码足足“占用”了三页半的篇幅，冲散了数学论证的重心。本着从简的原则，我们尝试使用通俗易懂的方法对代码，或者说，对算法，进行优化。

原命题（约瑟夫斯）

首先让我们先了解一下引入了概率条件的约瑟夫斯变种问题（简称变种问题）。

将排成一列的100个人从头开始，依此用从1开始的正整数编号，接着随机抽杀一个编号为奇数的人，之后序号的人顺序补位（例：第一次中抽中“杀死”97号，则原本的98,99,100号依次变为97,98,99号），随后对余下的人重复此操作，直至队伍中只剩最后一个人。问：初始编号为多少的人最安全？

数学问题很复杂，不过幸运的是这不是我们讨论的命题，我们需要实现的是用Python模拟抽杀的实验过程。

发现问题

我们期望得到的结果是初始编号为100的人最安全，同时整体上生存频率（多次实验后）与初始编号成正相关。在读明白变种问题后我们欣赏一下原文编者给出的模拟实验代码² ：

import itertools
import random
import numpy as np
from concurrent.futures import ProcessPoolExecutor, as_completed
import multiprocessing
import matplotlib.pyplot as plt
import tqdm

b = 100
count = np.zeros(b, dtype=int)
count_lock = multiprocessing.Lock()


def find_max_index(arr):
    max_index = 0
    for i in range(1, len(arr)):
        if arr[i] > arr[max_index]:
            max_index = i
    return max_index


def remove(numbers):
    n = random.randrange(0, len(numbers), 2)
    for i in range(n, len(numbers) - 1):
        numbers[i] = numbers[i + 1]
    numbers.pop()
    return numbers


def run_experiment(experiment_id):
    numbers = list(itertools.islice(itertools.count(1), b))
    while len(numbers) != 2:
        numbers = remove(numbers)
    return numbers[1]


def main():
    global count
    num_experiments = 100000  # 实验总次数
    num_processes = multiprocessing.cpu_count()  # 使用的进程数量，等于CPU核心数

    with ProcessPoolExecutor(max_workers=num_processes) as executor:
        futures = {executor.submit(run_experiment, i): i for i in range(num_experiments)}
        for future in tqdm.tqdm(as_completed(futures), total=num_experiments, desc="处理实验结果"):
            result = future.result()
            with count_lock:
                count[result - 1] += 1

    max_index = find_max_index(count) + 1
    print("Final count array:")
    print(count)
    print(f"Most frequent last number: {max_index}")

    # 绘制图表
    plt.figure(figsize=(10, 6))
    plt.bar(range(1, b + 1), count, color='blue')
    plt.xlabel('Number')
    plt.ylabel('Frequency')
    plt.title('Frequency of Each Number Being the Last Remaining')
    plt.grid(True)
    plt.savefig('number_frequency.png')  # 保存图表为文件
    plt.show()  # 显示图表


if __name__ == "__main__":
    main()

有意思的来了，试运行了一下，实际的结果输出是这样的：

到这里还是“可观”的，但到了画图的一步…

并没有得到图像的输出。实际上，原文中一开始也没有给出图像，而是在给出代码后这样说明：

请注意标蓝的那一行代码，我们在这里进行了一个着重的修改。它的意义是：当数列长度不为2（即数列中不只有两个数时），循环变种问题的操作；当数列长度为2时，停止循环操作，并输出第二项的初始位置。这种操作与正常循环变种问题是等价的。在附录中，我们会解释我们为什么进行了这样的修改。

然后编者进行了几次初始人数为10的预备实验，给出了1000000次实验后生存次数-编号图像³：

然而事实上，在附录中我发现其实编者团队在进行计算机实验的时候程序遇到了问题⁴，发现得到的10次实验中的数据为：

352. 1394. 1128. 1661.1211. 1340. 1018. 973. 581. 342.

他们“分析后认为，此代码的问题出在最后一次抽杀上：在最后一次抽杀时，程序会在第一象和第二项之间进行一个选择”，但至于“为什么当最后一次抽杀出现了问题之后，初始编号4立即成为了存活概率最高的位置”他们并没有合理的解释，只是说“受限于时间因素和篇幅因素，我们无法在本文中更加深入地探讨这一问题”并结束了文章⁵。

那么，如果我们对代码，或者说算法，进行优化……？

思路分析

我们看看Baidu Comate对源代码的注解：

注意：这个代码示例演示了如何使用并发和进程间同步来解决一个计算密集型的问题，并通过绘图库来可视化结果。然而，由于实验的数量和并发执行，这可能需要相当长的时间来完成，特别是在多核CPU上。

代码整体的思路并不复杂：

初始化变量：
- b：定义数字序列的上限，这里是100。
- count：一个长度为100的数组，用来记录每个数字作为最终结果的次数，初始值都为0。
- count_lock：一个锁，用来在多进程环境下保护count数组，确保数据的安全访问。
定义函数：
- find_max_index：这个函数用来找出count数组中最大值所在的索引，即哪个数字最终留下的次数最多。
- remove：这个函数模拟移除数字的过程，根据一个随机间隔来移除数字，直到剩下两个数字为止。
- run_experiment：这个函数执行一次实验，它创建一个从1到100的数字序列，然后不断调用remove函数直到剩下两个数字，最后返回第二个数字作为结果。
主函数（main）：
- 设置实验的总次数（100,000次）和并发进程的数量（等于CPU的核心数）。
- 使用ProcessPoolExecutor来并发执行实验。ProcessPoolExecutor会创建多个进程来并行运行run_experiment函数。
- 使用tqdm和as_completed来跟踪实验的完成情况。每当一个实验完成时，就获取其结果，并在count_lock的保护下更新count数组。
- 在所有实验完成后，使用find_max_index函数找出count数组中最大值所在的索引，并加1（因为数字是从1开始的），得到最终留下次数最多的数字。
- 使用matplotlib绘制一个条形图，展示每个数字作为最终结果的频率。
- 将图表保存为文件并显示出来。
运行代码：
- 直接运行这个脚本，就会调用main函数开始执行上述过程。

算法解析

简单拆解代码后我们发现，其实过程就是一个“编号——杀人——统计——重复——输出”的简单链式过程，并不值得调动函数、多进程并发复杂化处理。经我们简单分析后，短短26行代码（含注释）解决了绘图问题，同时并没有出现原编者所描述的最后一次抽杀数据不符现象。代码如下：

import random
import matplotlib.pyplot as plt

#开始鞭尸
a=[]
for i in range(1000000):
    #建立100个人的名单并以第一次编号给元素命名
    jsf = list(range(1,101))
    #开始杀人
    while len(jsf)>1:
        l=len(jsf)
        n=random.randrange(0,l,2)
        del jsf[n]
    a.append(jsf[0])

#输出结果
dict = {}    #字典统计
for key in a:
    dict[key]=dict.get(key,0)+1

#绘制柱状图
plt.bar(dict.keys(), height=dict.values())
plt.title('Who is the Safest?')
plt.xlabel('n')
plt.ylabel('v')

#显示图表
plt.savefig('frequency.png')
plt.show()
print(dict)

话先不多说，让我们试运行一下：
100000
很好，图表画出来了，而且，同是100000次实验，进程运行的时间被大大压缩。其实对比下来，不考虑画图过程，修改上述代码试验次数为1000000次，所消耗的时间甚至还比原文中程序运行100000次时间还要短一些，效率提升超10倍（100万次实验仅需约20秒⁶），这或许就是优化掉了并发执行的优势。下面是运行了100万次的图表：
1000000
也是进一步有助于原命题的猜想。
现在，让我们来仔细地讲解一下算法优化的核心思路。

导入

原文中是这样的：

import itertools   #用于迭代
import random    #随机抽数
import numpy as np    #核心运算
from concurrent.futures import ProcessPoolExecutor, as_completed    #并行执行
import multiprocessing    #多进程模块
import matplotlib.pyplot as plt    #绘图
import tqdm    #进度条

肉眼可见这里导入了一大堆module，那么他们对于我们目标的实现是否都是必须？这需要我们的思考。我想，或许原作者在发表原文的时候将数学论证作为核心，忘却了程序本身的目的性（生图），~~在使用ai生成实验代码的时候~~ 添加了很多过程性的功能，包括进程的实时显示。但我们都清楚，每多导入一个外部库，程序实际的启动时间包括电脑本身的内存占用都会有所提升。后续我们还发现，原作者在编译的过程中选择了函数调用的方式来运行，并且将运算交给了导入的模块，诚然增强了代码的可读性，但是同时增加了出错的概率。

接下来就让我们把多余的内容删掉：

import random
import matplotlib.pyplot as plt

没错，随机和绘图，这就是核心。

实验过程

原文先给定了个初始人数，并构设了一个数组：

b = 100
count = np.zeros(b, dtype=int)
count_lock = multiprocessing.Lock()

然后定义了一系列的函数：

def find_max_index(arr):
def remove(numbers):
def run_experiment(experiment_id):
# 然后处理
def main():

不能说错，很经典的处理方式，但……麻烦。于是，我们确定思路：

初始化：创建 1-100 的编号列表 [1, 2, 3, ..., 100]
特别地，为了区分初始编号与后面的实时编号，我们将列表中元素的名称记为初始编号，之后所在的索引（由于从零开始所以所选奇数实为偶数索引）为实时编号
循环判定：当列表长度 > 1 时继续淘汰
关键操作：
- 计算当前人数 L = len(jsf)
- 随机选择 偶数索引 n（对应奇数位置的人）
- 删除该索引处的元素（淘汰）
- 后续元素自动前移补位（隐式重新编号）
终止条件：当只剩 1 人时记录幸存者编号
重复实验：外部循环执行 100 万次并统计频率

以流程图的形式呈现如下：

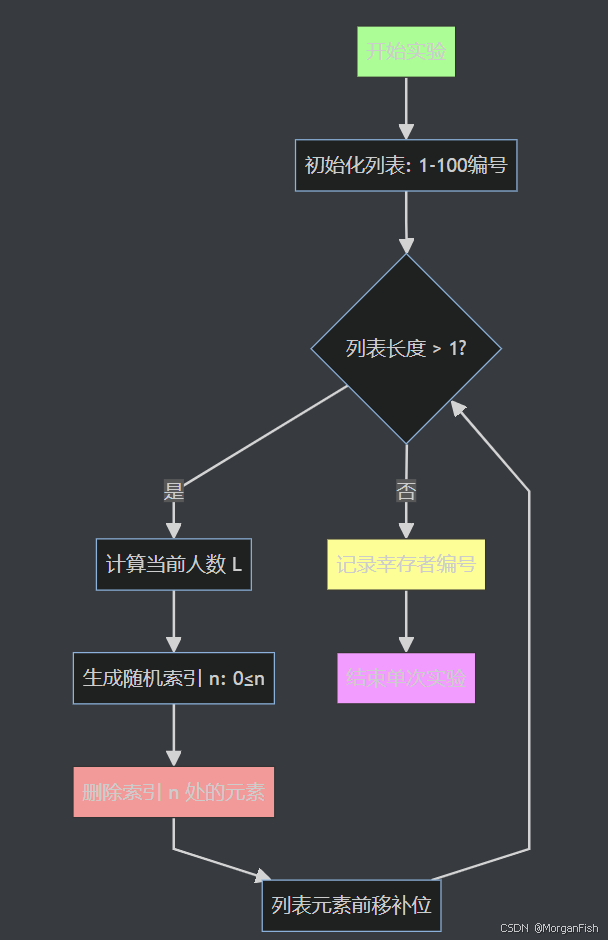
之后用代码呈现就理所当然了：

a=[]    # 准备一个容器盛装幸存者
for i in range(1000000):    # 构建实验次数
    # 建立100个人的名单并以第一次编号给元素命名
    jsf = list(range(1,101))
    # 开始杀人
    while len(jsf)>1:
        l=len(jsf)
        n=random.randrange(0,l,2)    # 由于步长为2，选择的就是偶数索引，对应命题中的奇数序号
        del jsf[n]    # 通过删除元素对应枪毙过程，同时实现了之后的人顺序补位
    a.append(jsf[0])    # 将最后幸存的元素添加到容器中以便后续统计

是不是也一目了然？

绘图

绘图其实就没什么好多说的了，无非是根据已知数据利用matplotlib.pyplot生成一幅棒状图罢了。不过，如何统计横纵坐标值得稍微思考一下。原文选择直接通过打印count数组直接绘图，其实也有另一种方法，非常简单。试问：Python中什么原生工具可以将数据与频数一一对应？没错，就是字典。

dict = {}    # 创建字典
for key in a:
    dict[key]=dict.get(key,0)+1    # 计数

然后直接画图：

plt.bar(dict.keys(), height=dict.values())
plt.title('Who is the Safest?')
plt.xlabel('n')
plt.ylabel('v')
# 存储并显示图表
plt.savefig('frequency.png')
plt.show()

然后你会在目录中看到生成的数据图。没错，就是上面文章中出现的几幅图。

回顾总结

做完以上的工作，我们可以发现“优化”这项工作并不是简单的代码润色；实际上，它是需要我们运用归纳思维将未知转化为已知。实际生活中我们常常会遇到需要我们优化的进程，我们需要铭记：学会改变我们思考的方式。在当下ai盛行的时代，回归根本往往是将复杂问题简单化处理的基础。在编程领域，这可能表现为将模糊的需求转化为清晰的函数模块；在生产生活中，则可能是将杂乱的操作步骤梳理成标准化的作业流程。因此，真正的优化过程始于人类思维的转变，在此基础上辅以技术工具的应用，才能实现从量变到质变的提升。

感谢阅读！（不介意的话可以要个小小的点赞嘛~）

这份报告同样发布于本人所在的研究性学习小组结题报告 ↩︎
原文可能由于排版出错导致有一些错乱，下面的代码是ds修正过的原本代码恢复版本，但代码内容未发生改变；同时还移除了未使用的导入的模块 ↩︎
源文档（顶部关联资源）中图片不好提取，因为我只有纸质稿，所以图像是根据我重新编写（优化后）的程序画出来的图像，含义和结果相同，后续会说明。原图可以见本报告顶部关联中的资源 ↩︎
详情见原报告图片 ↩︎
值得肯定的是，本文的数学论证思想值得研究与赞美，显然计算机程序不是他们设计的中心，因而产生了些许查错（严重怀疑ai生成代码），但是正是他们所留下的这个问题为我们的研究提供了方向 ↩︎
在i5-12450H上实测，优化后代码处理100万次仅19.3秒 ↩︎