数据结构之并查集：并查集的介绍与Python代码实现——18

并查集的介绍

• 并查集（Union-find）数据结构也称作合并查找集（Merge-find set）或者不相交集数据结构（disjoint-set data structure），它是一种记录了由一个或多个元素组成的不连续的分组的集合。并查集提供常数量的复杂度来添加、合并以及确定两个元素是否属于同一个集合。
• 并查集除了能够实现这些快速便利的操作，它在Krukal算法中寻找最小生成树的图也起着关键的作用
  
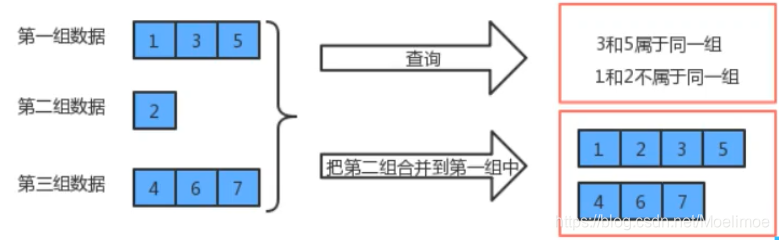
  并查集结构
  并查集是一种树形数据结构，但是它和二叉树、红黑树、B树不同，它对树形结构的要求十分简单：
  1. 同一个数据组中的元素对应在同一颗树（判断两个元素是否在同一颗树时，可以判断根结点是否相同）
  2. 同一数据组中的每一个元素对应树中的一个结点
  3. 不同数据组之间不存在任何相关的联系，可以看做多个数据组成一个森林（合并数据组时，只需要将一棵树的根结点指向另一颗树的根结点即可）
  4. 树中的结点不存在硬性的顺序/父子关系

并查集的功能实现

方法设计

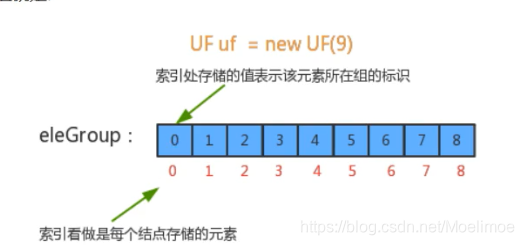
1. self.groups 是一个列表，其索引代表传入的元素的值，其元素代表传入元素所在分组
2. count_groups() 返回并查集中组的数量
3. which_group(item) 判断传入的元素item属于哪一个群组
4. in_the_same_group(item1, item2) 判断传入的两个元素是否在同一个分组
5. merge(item1, item2) 将两个元素各自所在的分组合并到一个组，合并后的分组为后者所在的组
   

Python代码实现

class UnionFind:
    def __init__(self, n):
        self.num_groups = n
        self.groups = [i for i in range(n)]  # Let the indices be the elements, and the elements be the group numbers

    def count_groups(self):
        return self.num_groups

    def which_group(self, item):
        """The indices are items, the elements are group numbers"""
        return self.groups[item]

    def in_the_same_group(self, item1, item2):
        return self.which_group(item1) == self.which_group(item2)

    def merge(self, item1, item2):
        group1 = self.which_group(item1)
        group2 = self.which_group(item2)
        if group1 == group2:
            return
        for i in range(len(self.groups)):
            if self.groups[i] == group1:
                self.groups[i] = group2
        self.num_groups -= 1

代码测试

if __name__ == '__main__':
    UF = UnionFind(5)

    print(f"The initial number of groups is {UF.num_groups}")
    print(f"The initial groups is {UF.groups}")

    while True:
        p = int(input(f'Input the to-be-merge element: '))
        q = int(input(f"Merge to the target element's group: "))

        if UF.in_the_same_group(p, q):
            print(f"They are already in the same group")
            continue
        UF.merge(p, q)
        print(f"The number of groups now is {UF.count_groups()}")
        print(UF.groups)

测试结果

The initial number of groups is 5
The initial groups is [0, 1, 2, 3, 4]
Input the to-be-merge element: 0
Merge to the target element's group: 1
The number of groups now is 4
[1, 1, 2, 3, 4]
Input the to-be-merge element: 1
Merge to the target element's group: 2
The number of groups now is 3
[2, 2, 2, 3, 4]
Input the to-be-merge element: 2
Merge to the target element's group: 3
The number of groups now is 2
[3, 3, 3, 3, 4]
Input the to-be-merge element: 3
Merge to the target element's group: 4
The number of groups now is 1
[4, 4, 4, 4, 4]
Input the to-be-merge element: 

最少需要n-1 = 4 次合并，就可以将所有元素都合并到一个分组到一个组。