HDU 6470 Count 【矩阵快速幂】（广东工业大学第十四届程序设计竞赛）

最新推荐文章于 2025-09-21 17:57:55 发布

原创最新推荐文章于 2025-09-21 17:57:55 发布 · 217 阅读

0 ·

CC 4.0 BY-SA版权

博客围绕一道题目展开，该题是矩阵快速幂类型，已给出递推式。解题关键在于构造转移矩阵，特别是处理 n 的 3 次方。最后给出了最终的转移矩阵和 AC 代码。

题目传送门：http://acm.hdu.edu.cn/showproblem.php?pid=6470

Count

Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 301 Accepted Submission(s): 127

Problem Description

Farmer John有n头奶牛.
某天奶牛想要数一数有多少头奶牛,以一种特殊的方式:
第一头奶牛为1号,第二头奶牛为2号,第三头奶牛之后,假如当前奶牛是第n头,那么他的编号就是2倍的第n-2头奶牛的编号加上第n-1头奶牛的编号再加上自己当前的n的三次方为自己的编号.
现在Farmer John想知道,第n头奶牛的编号是多少,估计答案会很大,你只要输出答案对于123456789取模.

Input

第一行输入一个T,表示有T组样例
接下来T行,每行有一个正整数n,表示有n头奶牛 (n>=3)
其中，T=10^4,n<=10^18

Output

共T行,每行一个正整数表示所求的答案

Sample Input

Sample Output

700

7486

64651

527023

Source

“字节跳动-文远知行杯”广东工业大学第十四届程序设计竞赛

解题思路：

很裸的一道矩阵快速幂的题，递推式都给出来了。

问题在于如何构造转移矩阵？也就是如何搞定 n 的3次方？

最终的转移矩阵：

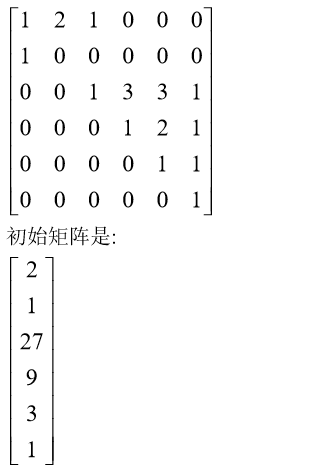
AC code：

 1 #include <bits/stdc++.h>
 2 #define INF 0x3f3f3f3f
 3 #define LL long long
 4 using namespace std;
 5 const int MAXN = 7;
 6 const LL MOD = 123456789;
 7 template<typename T, int N = 1>
 8 struct Matrix
 9 {
10     Matrix(int f = 0):n(sizeof(data[0])/sizeof(data[0][0])){
11         for(int i = 0; i < n; i++)
12             for(int j = 0; j < n; j++)
13                 data[i][j] = 0;
14         if(f)
15             for(int i = 0; i < n; i++) data[i][i] = T(1);
16     }
17 
18     Matrix operator * (const Matrix other) const{
19         Matrix<T, N> ret;
20         for(int i = 0; i < n; i++)
21             for(int j = 0; j < n; j++)
22                 for(int k = 0; k < n; k++)
23                 ret.data[i][j] = (ret.data[i][j] + data[i][k] * other.data[k][j]%MOD)%MOD;
24         return ret;
25     }
26 
27     Matrix operator + (const Matrix other) const{
28         Matrix<T, N> ret;
29         for(int i = 0; i < n; i++)
30             for(int j = 0; j < n; j++)
31             ret.data[i][j] = (data[i][j] + other[i][j])%MOD;
32         return ret;
33     }
34 
35     Matrix operator % (const LL MOD){
36         return *this;
37     }
38 
39     T data[N][N];
40     int n;
41 
42 };
43 
44 template<typename T>
45 T mul(T a, LL n, LL mod)
46 {
47     T ret(1);
48     for(; n ; n >>= 1){
49         ret = ret*(n&1 ? a:T(1)) %mod;
50         a = a*a%mod;
51     }
52     return ret;
53 }
54 
55 const LL modulu[MAXN][MAXN] = {
56     {1, 2, 1, 0, 0, 0},
57     {1, 0, 0, 0, 0, 0},
58     {0, 0, 1, 3, 3, 1},
59     {0, 0, 0, 1, 2, 1},
60     {0, 0, 0, 0, 1, 1},
61     {0, 0, 0, 0, 0, 1}
62 };
63 
64 int main()
65 {
66     std::ios::sync_with_stdio(false);
67     int T;
68     cin >> T;
69     for(LL n; T--; ){
70         cin >> n;
71         if(n <= 2){
72             cout << n << endl;
73             continue;
74         }
75         Matrix<LL, MAXN> a;
76         memcpy(a.data, modulu, sizeof(modulu));
77         a = mul(a, n-2, MOD);
78         cout << (a.data[0][0]*2 + a.data[0][1]*1 + a.data[0][2]*27 + a.data[0][3]*9 + a.data[0][4]*3 + a.data[0][5]*1)%MOD << endl;
79     }
80     return 0;
81 }