题目在这里就不再赘述,想看的话请参考上一篇【分治法】解决循环赛问题
看到网上关于循环赛问题提出过一种多边形法,感觉这个思路挺简单的,但是看别人代码没看懂,这里我简单分析几种情况然后写出自己理解的代码:
- n = 3,三边形如下:
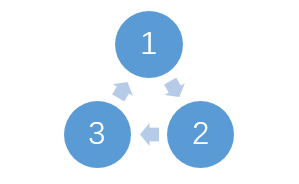
赛程安排如下:
第一天:(1,0) (2,3) //1轮空,2和3比赛,也可以表示为(3,2)
第二天:(2,0) (3,1) //2轮空,3和1比赛,也可以表示为(1,3)
第三天:(3,0) (1,2) //3轮空,1和2比赛,也可以表示为(2,1)
你看出有啥规律了吗,虽然我还没看出
这个其实就是每次以某一个运动员为对称轴,分割之后对称的一组比赛,剩下的一轮空也就是和0号组成一对。
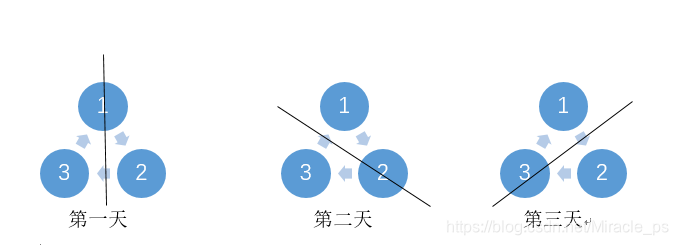
-
n = 4
对于偶数的情况,仅仅需要考虑奇数即可,就比如就可以用n=3来代替,然后将0换成4即可得到三天赛程(或者是“这个其实就是每次以某一个运动员为对称轴,分割之后对称的一组比赛,剩下的这个运动员也就和4号组成一对。”)
第一天:(1,4) (2,3)
第二天:(2,4) (3,1)
第三天:(3,4) (1,2) -
n = 5,五边形如下:
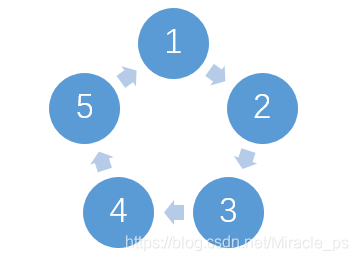
同理根据中心轴对称的原则来看:
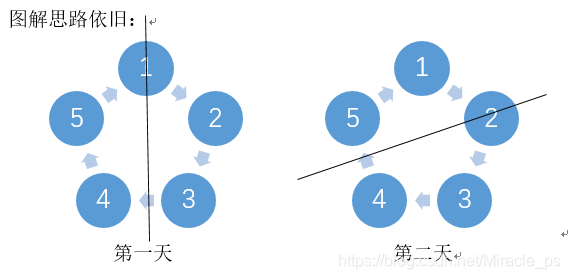
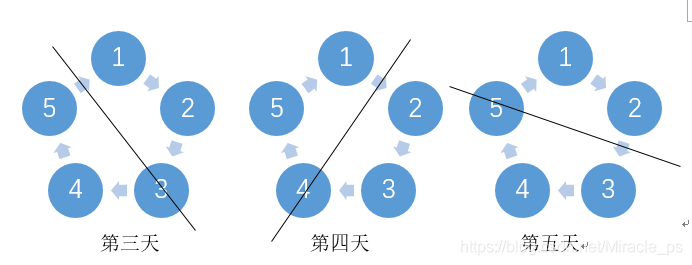
依然可以有以下安排:
第一天:(1,0) (2,5) (3,4)
第二天:(2,0) (3,1) (4,5)
第三天:(3,0) (4,2) (5,1)
第四天:(4,0) (5,3) (1,2)
第五天:(5,0) (1,4) (2,3)
看出规律了吗,看第一天和第二天,第二天和第三天,……第i天和第i+1天 -
n = 6类似,将0换成6即可得到安排
第一天:(1,6) (2,5) (3,4)
第二天:(2,6) (3,1) (4,5)
第三天:(3,6) (4,2) (5,1)
第四天:(4,6) (5,3) (1,2)
第五天:(5,6) (1,4) (2,3)
总结
那么问题来了,怎样用代码将以上问题描述出来呢,我们可以看到,对于n = 5中五天的赛程安排第二天就是在第一天的基础上循环加1(0不变,5 = (5 + 1)% 5, 其余的1、2、3、4自加就可以),对比之后其实所有的情况都是这样的,这样就可以经过n = 5次循环就得到所有的安排。
问题的合并考虑,对于所有情况,我们也像分治法一样全部转化为偶数情况(为了输出考虑),但是考虑问题得到时候用奇数多边形考虑(也就是考虑问题时候将以上的0全部换成相应的偶数,然后输出的时候依据情况而定)
算法设计
我们只需要分出第一天的安排就可以,然后其余的就根据规律一次求解。
对于n = 5,我们考虑数组[1,2,3,4,5,6],分成两半:对应关系就出来了:
第一天即为:(1,6) (2,5) (3,4)
然后其余赛程即是循环加法就可以(6不变,5 = (5 + 1)% 5, 1,2,3,4自加)完整代码如下:
# include <iostream>
using namespace std;
//多边形法--序列对
void Table(int n, int **a)
{
int m; //多边形边数
if(n % 2 == 0) m = n -1;
else m = n;
//int b[m][2];
int **b = new int *[m];//辅助序列数组
for(int i = 0;i < m; ++ i)
b[i] = new int[2];
for(int i = 1;i <= m + 1; i++)
{
a[i][1] = i;
}
for(int i = 2; i <= m+1; i ++)
{
int k, p, j;
if( i == 2)
for(j = 1; j <= (m + 1)/2; j ++)
{
//1-8 2-7 3-6 4-5
k = j;
p = m + 2 - j; //(k, p)
b[j][0] = k;
b[j][1] = p;
a[k][i] = p; //第1天预先设定好
a[p][i] = k;
}
else
for (j = 1; j <= (m + 1) / 2; j++)
{
if( b[j][0] == m - 1)
b[j][0] ++; //6
else if( b[j][0] == m + 1) ; //8
else
b[j][0] = (b[j][0] + 1) % m; //1~5 & 7
if( b[j][1] == m - 1)
b[j][1] ++;
else if( b[j][1] == m + 1) ;
else
b[j][1] = (b[j][1] + 1) % m;
k = b[j][0];
p = b[j][1]; //(k, p)
a[k][i] = p; //第i天:k VS p
a[p][i] = k;
}
}
for (int i = 0; i < m; ++i)
delete [] b[i];
delete [] b;
}
void display(int n, int **a)
{
if (n % 2 == 1) //n为奇数时候的输出
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n + 1; j++)
{
if (a[i][j] == n + 1)
cout << 0;
else
cout << a[i][j];
if (j == n + 1)
cout << endl;
else
cout << ' ';
}
}
else //n为偶数时候的输出
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cout << a[i][j];
if (j == n)
cout << endl;
else
cout << ' ';
}
}
}
int main()
{
int n;
cin >> n;
int **a = new int *[2 + n];
for (int i = 0; i < 2 + n; i++)
a[i] = new int[2 + n];
Table(n, a);
display(n, a);
for (int i = 0; i < 2 + n; i++)
delete [] a[i];
delete [] a;
return 0;
}
另外前面我说王晓东书上答案的那段代码如下,我其实没怎么看懂,但是感觉很nb,我试了试是可以解出答案的,我贴在下面
//多边形法--网上
void Table1(int n, int **p_array)
{
p_array[n][1] = n;
if (n == 1)
return;
int m = (n % 2 == 1) ? n : n - 1;
int b[m * 2];
int i, j, k, r;
for (i = 1; i <= m; ++i)
{
p_array[i][1] = i;
b[i] = i + 1;
b[m + i] = i + 1;
}
for (i = 1; i <= m; ++i)
{
p_array[1][i + 1] = b[i];
p_array[b[i]][i + 1] = 1;
for (j = 1; j <= m / 2; ++j)
{
k = b[i + j];
r = b[i + m - j];
p_array[k][i + 1] = r;
p_array[r][i + 1] = k;
}
}
}
测试样例
输入:只需输入整数n
输出:输出矩阵,第一列代表几号运动员,第二列到第n(n-1)列代表该天赛程(0表示改天轮空)
测试结果(均在vscode上面输出)
N = 3
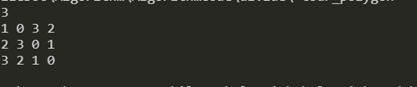
n = 7

n = 8
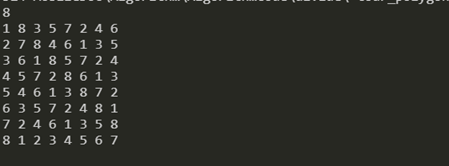





 本文介绍了一种使用多边形法解决循环赛赛程编排问题的算法,通过实例解析了不同人数下的赛程安排规律,并提供了一段C++代码实现。该算法适用于任意数量的参赛者,通过循环和模运算实现了赛程的自动生成。
本文介绍了一种使用多边形法解决循环赛赛程编排问题的算法,通过实例解析了不同人数下的赛程安排规律,并提供了一段C++代码实现。该算法适用于任意数量的参赛者,通过循环和模运算实现了赛程的自动生成。
















 421
421

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








