Dragonfly 拓扑的路由算法
John Kim, William J. Dally 等人在 2008 年的 ISCA 中提出技术驱动、高度可扩展的 Dragonfly 拓扑。而文章中也提到了 针对 Dragonfly 拓扑的路由算法。本文对其中提到的路由算法进行汇总归纳。主要是讨论蜻蜓拓扑的最小和非最小路由算法。
1. Dragonfly 上的路由
图 7 显示了如何使用虚拟通道 (VC) 来避免路由死锁。为了防止路由死锁,最小路由需要两个VC,非最小路由需要三个VC。此分配消除了由于路由而产生的所有通道依赖性。对于某些应用程序,可能需要额外的虚拟通道来避免协议死锁 - 例如,对于共享内存系统,请求和回复消息需要单独的虚拟通道集。
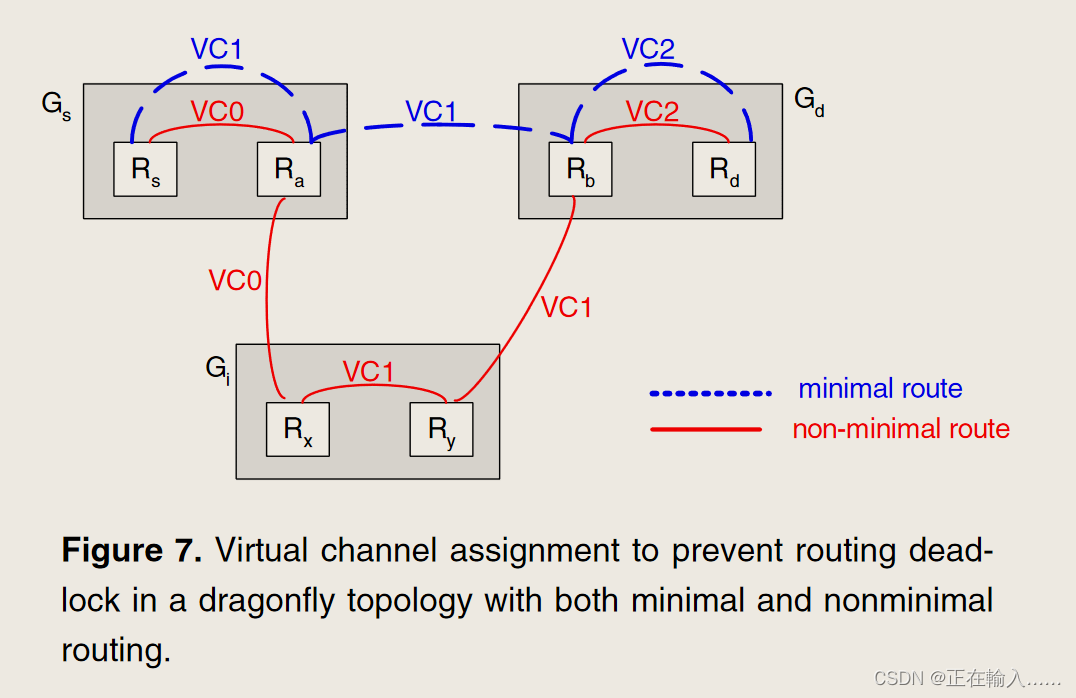
(1)最小路由
Dragonfly 中位于组Gs中的路由器Rs,连接着源节点s,到组Gd中的路由器Rd的目标节点d的最小路由经过单个全局通道,由三步组成:
- 步骤 1:如果 Gs != Gd,并且 Rs 没有到 Gd 的连接,在 Gs 内从 Rs 路由到 Ra,Ra 路由器具有到 Gd 的全局通道。
- 步骤 2:如果 Gs != Gd,则从 Ra 经过全局信道到达 Gd 中的路由器 Rb。
- 步骤 3:如果 Rb != Rd,则在 Gd 内从 Rb 到 Rd 路由。
这种最小路由非常适合负载平衡流量(load-balanced traffic),但会导致对抗性流量模式的性能非常差。
(2)非最小路由
为了对对抗性流量模式进行负载平衡,Valiant 的算法可以应用于系统级别 - 首先将每个数据包路由到随机选择的中间组 Gi,然后路由到其最终目的地 d。将 Valiant 的算法应用于组足以平衡全局和本地通道上的负载。这种随机非最小路由最多遍历两个全局通道,需要五个步骤:
- 步骤 1:如果 Gs != Gi 并且 Rs 没有到 Gi 的连接,则在 Gs 内从 Rs 路由到 Ra,一个具有到 Gi 的全局通道的路由器。
- 步骤 2:如果 Gs != Gi 从 Ra 经过全局信道到达 Gi 中的路由器 Rx。
- 步骤 3:如果 Gi != Gd 并且 Rx 没有到 Gd 的连接,则在 Gi 内从 Rx 路由到 Ry(具有到Gd 的全局通道的路由器)。
- 步骤 4:如果 Gi != Gd,则遍历从 Ry 到 Gd 中的路由器 Rb 的全局通道。
- 步骤 5:如果 Rb != Rd,则在 Gd 内从 Rb 到 Rd 路由。
2. 评估
实验评估最小路由算法 (MIN),Valiant (VAL)路由,UGAL 通用全局自适应负载平衡(UGAL-G,UGAL-L)。UGAL逐个数据包在 MIN 和 VAL 之间进行选择以平衡网络负载。通过使用队列长度和跳数来估计网络延迟并选择延迟最小的路径来做出选择。实验实现了两个版本的 UGAL:
- UGAL-L —— 使用当前路由器节点的本地队列信息。
- UGAL-G —— 使用 Gs 中所有全局通道的队列信息(原文中是使用 Gs 中所有全局通道的队列信息,但应该是具有全局信息)。假设了解其他路由器上的队列长度。虽然难以实现,但这代表了 UGAL 的理想实现,因为负载平衡需要全局通道,而不是本地通道。
理想的 UGAL 路由称为 UGAL-G(具有全局信息的 UGAL),假设精确的全局网络状态信息可用,并使用路径上所有链路上的总队列长度来估计路径上最小的数据包延迟。令 T Q M I N TQ_{MIN} TQMIN 为 M I N MIN MIN 路径的总队列长度, T Q V L B TQ_{VLB} TQVLB 为 V L B VLB VLB 路径的总队列长度。若
T Q M I N ≤ T Q V L B + T TQ_{MIN} \leq TQ_{VLB} + T TQMIN≤TQVLB+T
否则为 VLB 路径。这里的 T 是一个偏移常数,可以调整它来决定路径选择将在多大程度上偏向 MIN 路径(T 的较大值优先考虑 MIN 路径)。
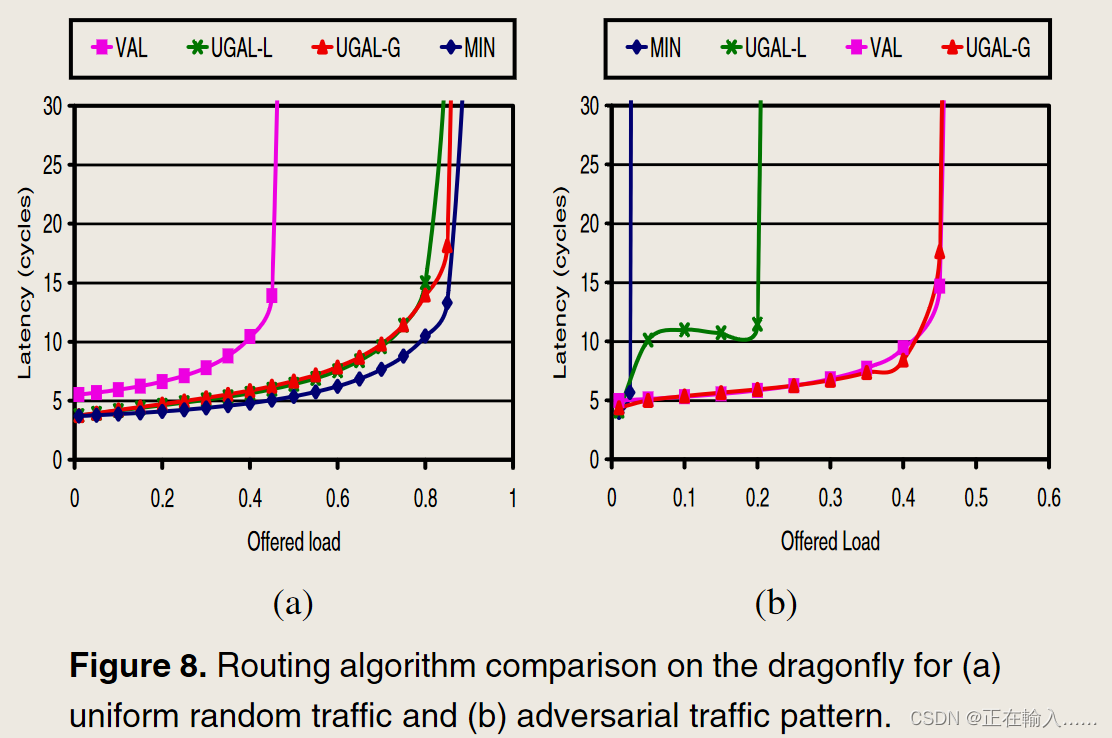
使用良性和对抗性合成流量模式来评估不同的路由算法。对于均匀随机 (UR) 等良性流量,MIN 足以提供低延迟和高吞吐量,如图 8(a)。 VAL 实现了大约一半的网络容量,因为它的负载均衡使全局通道上的负载加倍。UGAL-G 和 UGAL-L 都接近 MIN 的吞吐量,但在接近饱和时延迟稍高。较高的延迟是由使用并行或贪婪分配引起的,其中每个端口的路由决策是并行做出的。使用顺序分配将减少延迟,但代价是分配器更复杂。
为了测试路由算法的负载平衡能力,使用最坏情况 (WC) 流量模式,其中组 Gi 中的每个节点将流量发送到组 Gi+1 中随机选择的节点。通过最小路由,此模式将导致每个组 Gi 中的所有节点通过单个全局通道将其所有流量发送到组 Gi+1,需要非最小路由通过将大部分流量分散到其他全局通道来平衡此流量模式的负载。此 WC 流量的评估如图 8(b) 所示。由于 MIN 通过单个通道转发来自每个组的所有流量,因此其吞吐量限制为 1/ah。VAL 实现略低于 50% 的吞吐量,这是该流量的最大可能吞吐量。UGAL-G 实现了与 VAL 相似的吞吐量,但 UGAL-L 导致吞吐量有限,并且在中间负载时平均数据包延迟较高。
3. 存在问题
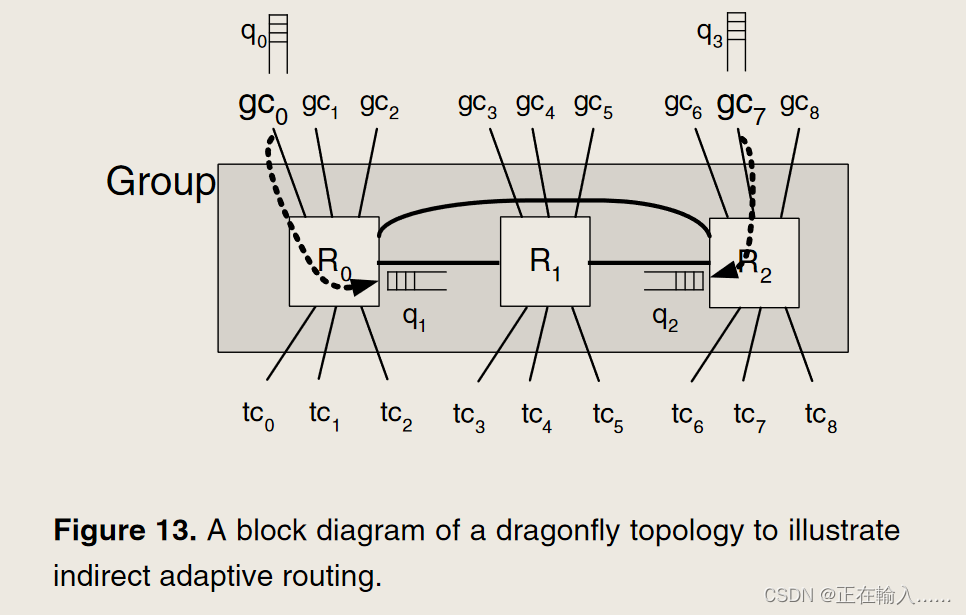
蜻蜓上的自适应路由具有挑战性,因为需要平衡的是全局通道、组输出,而不是路由器输出。这会导致间接路由问题(indirect adaptive routing)。以前的全局自适应路由方法使用本地队列信息、源队列和输出队列来生成网络拥塞的准确估计,本地队列是全局拥塞的准确代表,因为直接指示它们发起的路线上的拥塞。然而在蜻蜓拓扑中,本地队列只能通过本地通道上的反压来感知全局通道上的拥塞,并不准确。之前提到在WC流量模式下 UGAL-L 导致吞吐量有限,并且在中间负载时平均数据包延迟较高就是这个原因。
(1)吞吐量限制
UGAL-L 的吞吐量问题是由于单个本地通道同时处理最小和非最小流量造成的。例如在图 13 中,R1 中的数据包具有使用 gc7 的最小路径和使用 gc6 的非最小路径。这两条路径共享从 R1 到 R2 的相同本地通道。由于两条路径共享相同的本地队列(因此具有相同的队列占用率),并且最小路径较短(一跳与两跳),因此即使在饱和时,也始终会选择最小通道。这导致最小全局通道过载,并且与最小通道共享同一路由器的非最小全局通道未得到充分利用。
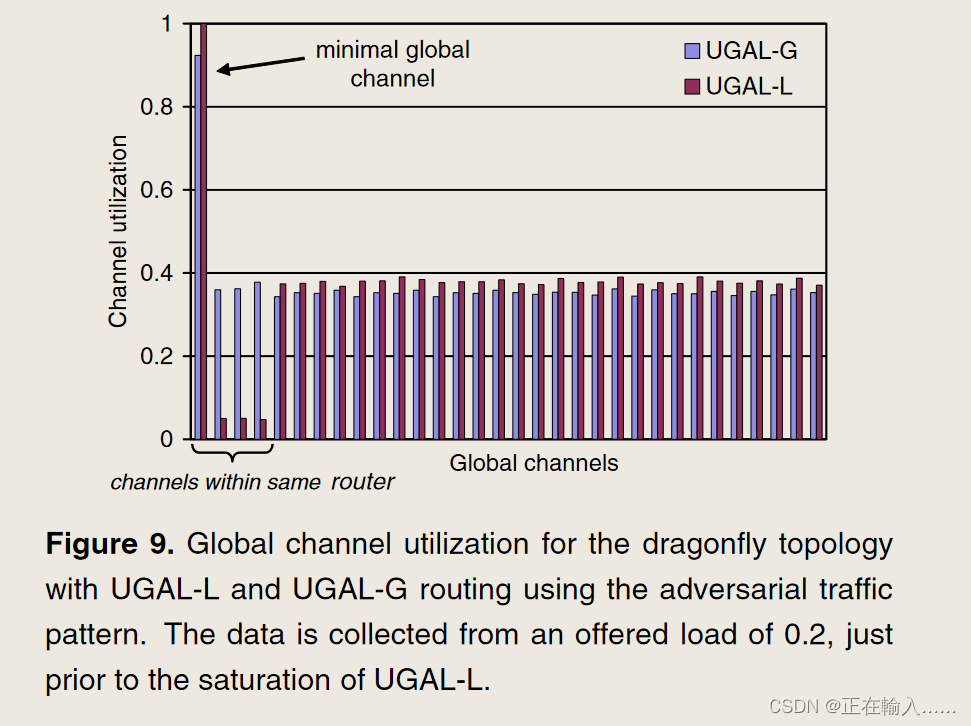
如图9所示。第一个全局通道是最小全局通道,接下来的三个全局通道是与最小通道共享同一路由器的非最小通道(h = 4),其余通道是共享同一组的非最小通道。对于 UGAL-G,最小通道是首选,并且负载在所有其他全局通道之间均匀平衡。另一方面,对于 UGAL-L,路由器上包含最小全局信道的非最小信道未得到充分利用,从而导致网络吞吐量下降。为了克服这个限制,我们修改了 UGAL 算法,通过使用单独的 VC (UGAL-LVC) 将队列占用率分成最小和非最小分量。

这种修改对于大部分流量需要非最小化发送的 WC 流量,UGALLVC 表现良好,因为最小队列负载很重。然而,对于负载平衡流量来说,当大多数流量应以最低限度发送时,各个 VC 无法提供通道拥塞的准确表示,从而导致吞吐量下降。为了克服这个限制,我们进一步修改 UGAL 算法,仅当最小和非最小路径以相同的输出端口开始时,将队列占用分为最小和非最小分量。我们的混合修改 UGAL 路由算法 (UGAL-LVC H ) 是

与 UGAL-LVC 相比,UGAL-LVC H 在 WC 流量模式上提供相同的吞吐量,在 UR 流量上与 UGAL-G 的吞吐量匹配,但在提供的 0.8 负载(接近饱和)下导致延迟高出近 2 倍。对于 WC 流量,与 UGAL-G 相比,UGAL-LVC H 还会导致更高的中间延迟(图 10(b))。
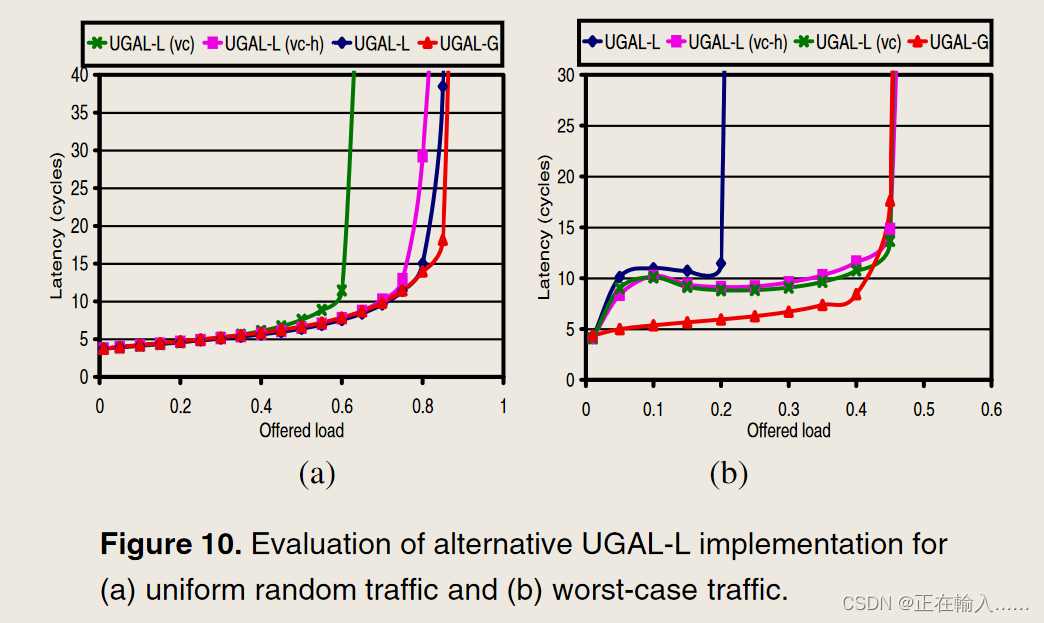
(2)较高的中间延迟
UGAL-L 的较高中间延迟是由于在检测到拥塞之前最小路由数据包必须填充源和拥塞点之间的通道缓冲区。如图13所示在此示例中,q1 反映 q0 的状态,q2 反映 q3 的状态。当 q0 或 q3 已满时,流量控制向 q1 和 q2 提供背压,如图 13 中的箭头所示。因此,在稳定状态下-状态测量,这些本地队列信息可以用来精确测量吞吐量。由于吞吐量被定义为当延迟达到无穷大(或队列占用率达到无穷大)时提供的负载,因此这个本地队列信息就足够了。然而,q0 需要完全满,以便 q1 反映 gc0 的拥塞情况并允许 R1 非最小路由数据包。因此,使用本地信息需要牺牲一些数据包来正确确定拥塞情况,从而导致以最低限度发送的数据包具有更高的延迟。随着负载的增加,尽管最小路由数据包的延迟持续增加,但更多数据包以非最小路由方式发送,导致平均延迟减少直至饱和。**为了使本地队列能够对全局拥塞提供良好的估计,全局队列需要完全满,并向本地队列提供严格的背压。反压的刚度与缓冲区的深度成反比——缓冲区越深,反压传播所需的时间就越长,而缓冲区越浅,提供的反压就越硬。**缓冲区大小变化时的仿真结果如图 14 所示。
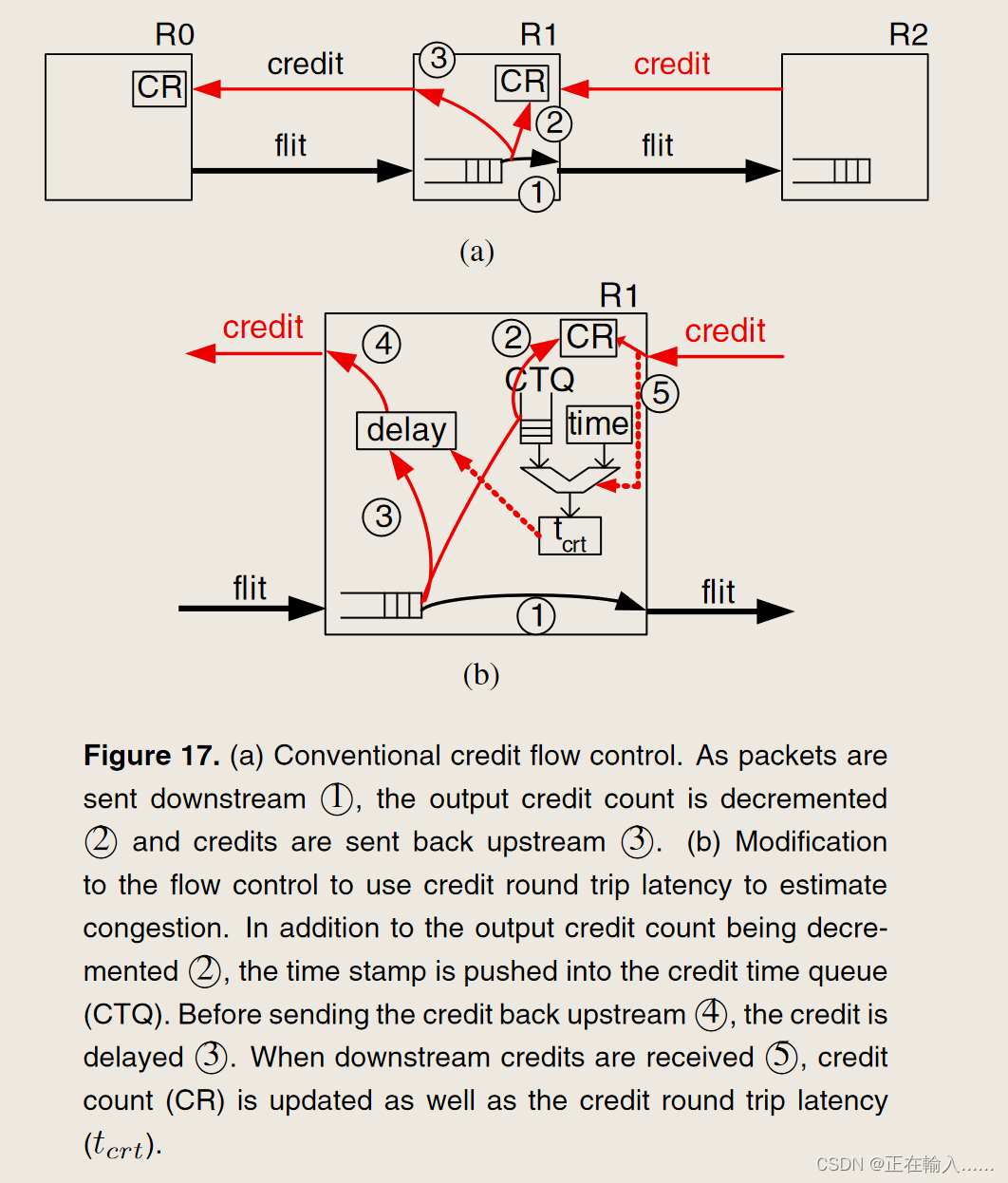
为了克服高中间延迟,建议使用信用往返延迟来更快地感知拥塞并减少延迟。 tcrt的值可以用来估计全局信道的拥塞情况。通过使用此信息来延迟上游信用,我们加强了背压并更快地向上游传播拥塞信息。对于每个输出 O,测量 tcrt(O),并将数量 td(O)=tcrt(O) − tcrt0 存储在寄存器中。然后,当一个 flit 被发送到输出 O 时,不是立即将信用值发送回上游,而是将信用值延迟 td(O) − min[td(o)]。通过全球渠道发送的积分不会延迟。这保证了该机制中不存在循环,并允许全局通道得到充分利用。返回积分的延迟提供了较浅缓冲区的出现,从而产生了硬的背压。
references
[1] J. Kim, W. J. Dally, S. Scott, and D. Abts, “Technology-Driven, Highly-Scalable Dragonfly Topology,” in 2008 International Symposium on Computer Architecture, Beijing, China: IEEE, Jun. 2008, pp. 77–88. doi: 10.1109/ISCA.2008.19.







 文章详细介绍了Dragonfly拓扑的最小和非最小路由算法,以及UGAL路由策略。评估结果显示最小路由在负载平衡方面表现良好,但对对抗性流量模式不利。非最小路由通过随机选择中间组进行负载均衡,但存在吞吐量限制和较高的中间延迟。后续的UGAL算法优化解决了部分问题,但仍需考虑全局拥塞感知和信用往返延迟来降低延迟。
文章详细介绍了Dragonfly拓扑的最小和非最小路由算法,以及UGAL路由策略。评估结果显示最小路由在负载平衡方面表现良好,但对对抗性流量模式不利。非最小路由通过随机选择中间组进行负载均衡,但存在吞吐量限制和较高的中间延迟。后续的UGAL算法优化解决了部分问题,但仍需考虑全局拥塞感知和信用往返延迟来降低延迟。

















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










