《LeetCode之每日一题》：64.最小好进制

有关题目

对于给定的整数 n, 如果n的k（k>=2）进制数的所有数位全为1，则称 k（k>=2）是 n 的一个好进制。

以字符串的形式给出 n, 以字符串的形式返回 n 的最小好进制。

示例 1：

输入："13"
输出："3"
解释：13 的 3 进制是 111。

示例 2：

输入："4681"
输出："8"
解释：4681 的 8 进制是 11111。

示例 3：

输入："1000000000000000000"
输出："999999999999999999"
解释：1000000000000000000 的 999999999999999999 进制是 11。

提示：

n的取值范围是 [3, 10^18]。
输入总是有效且没有前导 0。

题解

法一：数学
参考官方题解

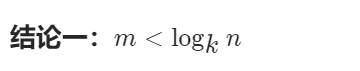
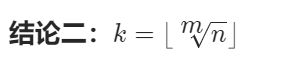
class Solution {
public:
    string smallestGoodBase(string n) {
        long nVal = stol(n);//参数提供的字符串转换为long int
        int mMax = floor(log(nVal) / log (2));//y = floor(x)。则y等于：不大于x的最大整数。
        for (int m = mMax; m > 1; m--)//根据对数函数的单调性，这边k其实就是从 2开始从小到大
        //寻找满足条件的最小好进制
        {
            int k = pow(nVal,1.0 / m);
            long mul = 1,sum = 1;//sum = 1把最后一位1包含进去了
            for (int i = 0; i < m; i++)
            {
                mul *= k;//计算出最后一位1外其他位之和
                sum += mul;
            }
            if (sum == nVal)   
                return to_string(k);
        }
        //m = 1 直接返回 k = n - 1;
        return to_string(nVal - 1);
    }
};