CRT+LUCAS+EX欧拉 古代猪文

求这个东西

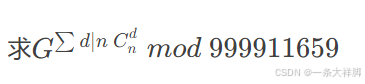
指数取模，想到欧拉定理，注意到模数是个比底数大的质数，底数和模数肯定是互质的，并且模数是个指数，$m$的欧拉函数值就是$m-1$。那么$a^b\mathrm{mod}m$等价于$a^{b\mathrm{mod}m-1}\mathrm{mod}m$

于是转化为求$b\mathrm{mod}m-1$，现在的问题是$m-1$不是质数了，但它可以分解成几个质数的一次方，这种取模一般就考虑先分别求出对每个质因子的余数，然后用中国剩余定理，就能求出来对原模数的余数。

那么下一步的问题是怎么求出来$b\mathrm{mod}fa{c}_i$，也就是求出来指数对于每个质因子的余数，注意到质因子不大，并且指数是个组合数求和，考虑$lucas$定理

需要注意的是，求一个质因子的余数时，$lucas$的模数都是固定的，只用预处理一次

long long CRT(vi& W,vi& B,int k/*方程组数*/){
	long long x,y,a=0,m,n=1;
	for(long long i=0;i<k;i++) n*=W[i];
	for(long long i=0;i<k;i++){
		m=n/W[i];
		a=(a+B[i]*m%n*power(m,W[i]-2,W[i])%n)%n;
	}
	return a>0?a:a+n;
}
vi fa(N);
void init(int n,int p){
	fa[0]=1;
	rep(i,1,n){
		fa[i]=fa[i-1]*i%p;
	}
}
int lucas(int n,int m,int p){
	auto C=[&](int n,int m,int p)->int{
		if(n<m)return 0;
		return fa[n]*power(fa[m],p-2,p)%p*power(fa[n-m],p-2,p)%p;
	};
	auto &&lu=[&](auto &&lu,int n,int m,int p)->int{
		if(n<m)return 0;
		if(m==0)return 1;	
		return C(n%p,m%p,p)*lu(lu,n/p,m/p,p)%p;
	};
	return lu(lu,n,m,p);
}
void solve() {
    int n,g;
    cin>>n>>g;
    vi d={2,3,4679,35617};
    vi r;
    int mod=999911659;
    rep(i,0,3){
    	init(d[i],d[i]);
    	int sum=0;
		rep(j,1,sqrt(n)){
			if(n%j==0){
				sum+=lucas(n,j,d[i]);
				sum%=d[i];
				if(n/j!=j){
					sum+=lucas(n,n/j,d[i]);
					sum%=d[i];
				}
			}
		}
		r.push_back(sum);
	}
	int res=CRT(d,r,4);
	cout<<power(g,res,mod);
}