【HMM预测】基于HMM隐马尔可夫模型的金融数据预测算法matlab仿真

✅作者简介：热爱数据处理、建模、算法设计的Matlab仿真开发者。

🍎更多Matlab代码及仿真咨询内容点击 🔗：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

在金融市场这片波涛汹涌的大海里，投资者们如同勇敢的航海家，渴望找到准确预测市场走势的 “宝藏地图”。就拿股票市场来说，无数投资者每日紧盯股票价格走势，试图从那起起伏伏的曲线中，找到未来价格变化的蛛丝马迹，预测股票价格明天是涨是跌、下周会如何波动，以此来决定自己的投资决策，获取丰厚的收益 。

而在众多探索金融数据预测的道路上，隐马尔可夫模型（Hidden Markov Model，HMM）宛如一张独特而神秘的 “隐形地图”，逐渐崭露头角，吸引了众多研究者和投资者的目光。简单来说，HMM 是一种统计模型，它主要用于描述一个含有隐含未知参数的马尔可夫过程。这里面有两个关键概念，一个是 “隐含未知参数”，就好比在股票市场中，股票价格的涨跌看似杂乱无章，但背后其实受到许多隐藏因素的影响，如公司的内部管理、宏观经济形势、行业竞争态势等，这些因素我们很难直接观测到，却对股票价格有着重要作用，这就是 HMM 中的 “隐含” 部分；另一个是 “马尔可夫过程”，它有个很有趣的特性，即下一时刻的状态只依赖于当前时刻的状态，而与过去的状态无关。想象一下你在玩大富翁游戏，你下一次走到哪个格子，只取决于你当前所在的格子和骰子的点数，而和你之前走过哪些格子没有关系，这就是简单的马尔可夫过程示例，在 HMM 里，金融数据的状态转移也遵循类似的规律。

探秘 HMM：工作原理大起底

（一）核心组件剖析

要深入了解 HMM 这张 “隐形地图” 是如何引导我们在金融数据的海洋中航行的，就必须剖析它的核心组件 。

1. 隐藏状态（Hidden States）：这是 HMM 中最为神秘的部分，就如同幕后的操纵者，虽不直接露面，却掌控着一切。在金融市场里，隐藏状态可以代表市场的不同趋势阶段，比如牛市、熊市或者震荡市。以股票市场为例，一只股票的价格走势背后，可能隐藏着市场对该公司未来盈利预期的不同状态，也许是市场普遍预期公司未来盈利大幅增长，处于乐观的 “牛市状态”；也许是预期公司将面临困境，盈利下滑，处于悲观的 “熊市状态”，但这些状态我们无法直接观测到，只能通过一些外在的表现来推测。

1. 观测序列（Observation Sequence）：与隐藏状态相对应，观测序列是我们能够直接观察和获取的数据。在金融领域，最常见的观测序列就是各种金融时间序列数据，如股票价格、成交量、汇率等。还是以股票市场来说，我们每天都能从财经媒体、交易软件上获取某只股票的收盘价，这些收盘价就构成了一个观测序列 。通过对这些可见的观测序列进行分析，我们试图揭开背后隐藏状态的秘密。

1. 状态转移概率矩阵（State Transition Probability Matrix）：它描述了系统从一个隐藏状态转移到另一个隐藏状态的概率。用数学语言来说，如果有 N 个隐藏状态，那么状态转移概率矩阵就是一个 N×N 的方阵，矩阵中的元素 Aij 表示在当前时刻处于状态 i 的情况下，下一个时刻转移到状态 j 的概率。在股票市场的例子中，假设市场只有牛市（状态 1）和熊市（状态 2）两种隐藏状态，那么状态转移概率矩阵中的 A11 就表示当前处于牛市时，下一个阶段仍然处于牛市的概率；A12 则表示当前处于牛市时，下一个阶段转变为熊市的概率。这个矩阵反映了市场状态之间的动态变化规律，对于预测市场未来趋势至关重要 。

1. 观测概率矩阵（Observation Probability Matrix）：也叫发射概率矩阵，它表示在每个隐藏状态下，产生各种观测值的概率。同样，若有 N 个隐藏状态和 M 种可能的观测值，观测概率矩阵就是一个 N×M 的矩阵，其中元素 Bij 表示在状态 i 下，观测到值 j 的概率。继续以股票为例，在牛市状态下，股票价格上涨（观测值 1）、下跌（观测值 2）或者持平（观测值 3）都有各自不同的概率，这些概率就构成了观测概率矩阵中对应牛市状态的那一行元素 。通过这个矩阵，我们建立起了隐藏状态与观测序列之间的概率联系。

（二）关键假设解读

HMM 能够在金融数据预测中发挥作用，离不开两个重要的假设，它们就像是 HMM 运行的基石。

1. 马尔可夫性质（Markov Property）：这个性质可以简单理解为 “未来只依赖于现在，而与过去无关”。在 HMM 的世界里，它意味着系统在 t 时刻的隐藏状态只取决于 t - 1 时刻的隐藏状态，与 t - 2 及更早时刻的状态没有直接关系。回到金融市场的例子，在预测股票价格明天的走势时，根据马尔可夫性质，我们主要关注今天股票价格所处的状态（是上涨、下跌还是横盘）以及当前市场的整体状态（牛市、熊市或震荡市），而不需要过多考虑昨天或者上周的价格走势细节。虽然在现实中金融市场并非完全严格遵循马尔可夫性质，过去的很多因素实际上也会对未来产生影响，但马尔可夫性质的假设在一定程度上简化了模型的复杂度，使得我们能够在有限的信息下对未来进行合理的预测 。

1. 输出独立性假设（Output Independence Assumption）：该假设表明在每个时刻，观测值仅依赖于当前时刻的隐藏状态，与其他时刻的观测值和隐藏状态都无关。以股票市场为例，今天股票的收盘价只取决于当天市场所处的隐藏状态（比如是牛市还是熊市），而与昨天的收盘价以及前天市场处于什么状态没有直接的概率依赖关系。这个假设使得我们在处理观测序列时更加便捷，能够将每个时刻的观测值看作是独立产生的，从而可以基于当前的隐藏状态来计算观测值出现的概率 。但同样，在实际金融市场中，这种独立性假设并不完全成立，股票价格之间往往存在一定的相关性和趋势延续性，但在 HMM 模型中，为了模型的可解性和实用性，我们做了这样的简化假设。

这两个假设虽然在一定程度上对复杂的金融市场进行了简化，但正是基于它们，HMM 才构建起了一套完整的、可用于金融数据预测的理论框架，帮助我们从看似杂乱无章的金融数据中挖掘出潜在的规律和趋势。

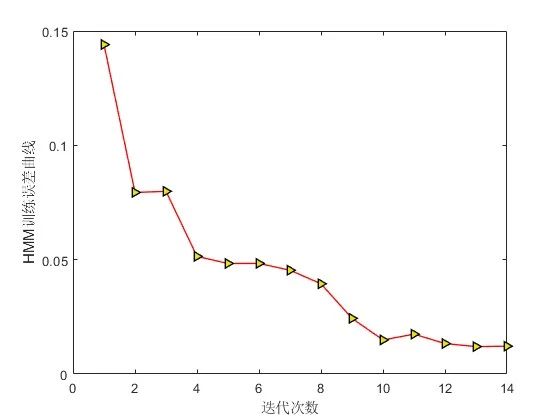
⛳️ 运行结果

🔗 参考文献

🎈 部分理论引用网络文献，若有侵权联系博主删除

本主页优快云博客涵盖以下领域：

🌈 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱调度、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划（2E-VRP）、充电车辆路径规划（EVRP）、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题、港口调度、港口岸桥调度、停机位分配、机场航班调度、泄漏源定位

🌈 机器学习和深度学习时序、回归、分类、聚类和降维

2.1 bp时序、回归预测和分类

2.2 ENS声神经网络时序、回归预测和分类

2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类

2.4 CNN|TCN|GCN卷积神经网络系列时序、回归预测和分类

2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类

2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类

2.7 ELMAN递归神经网络时序、回归\预测和分类

2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类

2.9 RBF径向基神经网络时序、回归预测和分类

2.10 DBN深度置信网络时序、回归预测和分类

2.11 FNN模糊神经网络时序、回归预测

2.12 RF随机森林时序、回归预测和分类

2.13 BLS宽度学习时序、回归预测和分类

2.14 PNN脉冲神经网络分类

2.15 模糊小波神经网络预测和分类

2.16 时序、回归预测和分类

2.17 时序、回归预测预测和分类

2.18 XGBOOST集成学习时序、回归预测预测和分类

2.19 Transform各类组合时序、回归预测预测和分类

方向涵盖风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、用电量预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

🌈图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

🌈 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、 充电车辆路径规划（EVRP）、 双层车辆路径规划（2E-VRP）、 油电混合车辆路径规划、 船舶航迹规划、 全路径规划规划、 仓储巡逻

🌈 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化、车辆协同无人机路径规划

🌈 通信方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化、水声通信、通信上传下载分配

🌈 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化、心电信号、DOA估计、编码译码、变分模态分解、管道泄漏、滤波器、数字信号处理+传输+分析+去噪、数字信号调制、误码率、信号估计、DTMF、信号检测

🌈电力系统方面

微电网优化、无功优化、配电网重构、储能配置、有序充电、MPPT优化、家庭用电

🌈 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 金属腐蚀

🌈 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合、SOC估计、阵列优化、NLOS识别

🌈 车间调度

零等待流水车间调度问题NWFSP 、 置换流水车间调度问题PFSP、 混合流水车间调度问题HFSP 、零空闲流水车间调度问题NIFSP、分布式置换流水车间调度问题 DPFSP、阻塞流水车间调度问题BFSP