【参数估计】基于Volterra积分算子的固定时间自适应参数估计算法实现Chua混沌电路固定时间自适应参数估计附Matlab代码-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab_dashi/article/details/148493335

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎 往期回顾关注个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🔥 内容介绍

在科学的广袤领域中，混沌现象宛如一颗神秘而璀璨的星辰，吸引着无数研究者的目光。从大气中捉摸不定的气象变化，到生物系统里微妙复杂的生命活动，混沌现象无处不在，深刻地影响着我们对世界的认知。混沌，这一非线性科学中的重要概念，打破了传统科学中关于确定性和可预测性的固有观念，揭示了在看似随机无序的表象下，隐藏着的深层确定性规律。

Chua 混沌电路，作为混沌研究领域的一颗明珠，于 1983 年由蔡少棠教授发表，当时他正在日本早稻田大学担任访问学者。因其简单的电路结构和典型的混沌特性，成为了研究混沌现象的经典范例，被誉为 “混沌系统的典范”。这个电路仅由几个基本的电子元件组成，却能展现出极为复杂的混沌行为，就像是一个微观的宇宙，蕴含着无尽的奥秘，为我们深入理解混沌现象提供了一个直观而有效的平台。通过电磁学定律，蔡氏电路可以被准确地建立数学模型，用一组耦合的非线性微分方程来描述其动力学特性，这使得对其进行理论分析和数值模拟成为可能。

在 Chua 混沌电路的研究和应用中，准确的参数估计是至关重要的环节，就如同为混沌电路这台精密仪器校准刻度。电路中的参数，如电阻、电容、电感等，它们的精确值直接影响着电路的混沌行为和性能表现。在通信领域，利用 Chua 混沌电路进行信号加密时，参数的准确性决定了加密的强度和安全性；在混沌控制中，只有准确掌握电路参数，才能实现对混沌状态的有效调控，使电路按照我们期望的方式运行。

传统的参数估计方法在面对复杂的混沌系统时，往往显得力不从心。而固定时间自适应参数估计方法的出现，为混沌电路的参数估计带来了新的曙光。与传统方法相比，它具有独特的优势。在收敛速度方面，固定时间自适应参数估计方法能够在更短的时间内达到收敛，大大提高了参数估计的效率，就像是一辆高速行驶的汽车，能够更快地到达目的地。而且，其收敛时间不依赖于初始条件，这使得在不同的初始状态下，都能稳定、可靠地完成参数估计，如同一位坚定的行者，不受外界干扰，始终朝着目标前进。这种稳定性和可靠性，为混沌电路在各种实际应用中的稳定运行提供了坚实的保障。

Volterra 积分算子：核心钥匙的解析

在我们探索 Chua 混沌电路固定时间自适应参数估计的征程中，Volterra 积分算子无疑是一把至关重要的核心钥匙。它为我们打开了一扇通往更高效、更精确参数估计的大门，让我们能够在混沌的世界中捕捉到那些隐藏的参数信息。

Volterra 积分算子，作为数学分析中的一个重要概念，具有独特的性质和广泛的应用。它的基本定义为：对于定义在区间\([a,b]\)上的函数\(f(t)\)，Volterra 积分算子\(V_k\)对其的作用结果\([V_kf](t)\)为\(\int_{a}^{t}k(t,\tau)f(\tau)d\tau\)，其中\(k(t,\tau)\)被称为核函数，它就像是 Volterra 积分算子的 “灵魂”，决定着算子的具体行为和作用效果。

在参数估计的领域中，Volterra 积分算子发挥着不可或缺的作用。它能够将复杂的系统方程进行巧妙的变换，把一些难以直接处理的未知量通过积分运算进行转化，从而为我们设计参数估计器提供便利。就如同一位神奇的魔术师，能够将看似杂乱无章的信息整理得井井有条，让我们能够从中找到解决问题的线索。

为了更好地实现固定时间自适应参数估计，我们需要巧妙地选取核函数\(k(t,\tau)\)，使其满足特定的条件。经过深入的研究和分析，我们发现当核函数\(k(t,\tau)\)满足在\(\tau = 0\)和\(\tau = t\)时，核函数及其导数为零，即\(k^{(i)}(t,t) = 0\)且\(k^{(i)}(t,0) = 0\)（\(i\)表示导数的阶数），能够带来诸多优势。

这种特殊的核函数选择，就像是为我们的参数估计之旅铺设了一条平坦的道路。它能够有效地消除系统初始值的影响，使得我们的参数估计结果更加稳定和可靠。在实际的混沌电路中，初始值往往是难以精确确定的，而 Volterra 积分算子通过这种巧妙的核函数选取，成功地避开了这个难题，让我们的参数估计不再受到初始值的干扰，就如同在茫茫大海中航行的船只，不再被风浪所左右，能够坚定地朝着目标前进。

同时，这样的核函数选择还避免了对系统输出导数的计算。在实际应用中，计算系统输出导数不仅复杂繁琐，还容易引入误差，而 Volterra 积分算子的这一特性，大大简化了计算过程，提高了参数估计的效率和准确性。它就像是一位智慧的工匠，用巧妙的方法简化了复杂的工艺，让我们能够更轻松地完成参数估计的任务。

Chua 混沌电路数学建模：搭建研究基石

在深入探索基于 Volterra 积分算子的固定时间自适应参数估计算法对 Chua 混沌电路的应用之前，我们首先需要深入了解 Chua 混沌电路的数学建模，这是我们后续研究的基石，为我们理解电路的行为和特性提供了关键的线索。

Chua 混沌电路的拓扑结构相对简洁，却蕴含着复杂的动力学奥秘。它主要由两个电容（\(C_1\)和\(C_2\)）、一个电感（\(L\)）、一个线性电阻（\(R\)）以及一个关键的非线性电阻（蔡氏二极管）构成。当电路通电后，电流在这些元件之间流动，电容储存和释放电荷，电感阻碍电流的变化，而蔡氏二极管则以其独特的非线性特性，打破了电路中原本可能存在的简单线性关系，为混沌现象的产生创造了条件。

通过严谨的电路分析和电磁学定律，我们可以将 Chua 混沌电路的行为转化为精确的数学语言。以电容\(C_1\)和\(C_2\)两端的电压\(u_{C1}\)、\(u_{C2}\)以及电感\(L\)上的电流\(i_{L}\)作为状态变量，建立起描述 Chua 混沌电路的微分方程组：\( \begin{cases} C_1\frac{du_{C1}}{dt} = G(u_{C2} - u_{C1}) - g(u_{C1}) \\ C_2\frac{du_{C2}}{dt} = G(u_{C1} - u_{C2}) + i_{L} \\ L\frac{di_{L}}{dt} = -u_{C2} \end{cases} \)

其中，\(G = \frac{1}{R}\)为电导，\(g(u_{C1})\)是非线性电阻的电流 - 电压特性函数，通常表现为分段线性函数，它就像是电路中的 “魔法开关”，在不同的电压区间展现出不同的电阻特性，使得电路的行为变得复杂而多变。

为了进一步简化分析，我们引入无量纲化处理，这是一种在科学研究中常用的技巧，就像是给复杂的问题穿上一件简洁的外衣。通过适当的变量替换，将实际的物理量转化为无量纲的量，使得方程的形式更加简洁，便于我们进行深入的理论分析和数值计算。经过无量纲化处理后，Chua 混沌电路的数学模型变为：\( \begin{cases} \frac{dx}{dt} = \alpha(y - x - f(x)) \\ \frac{dy}{dt} = x - y + z \\ \frac{dz}{dt} = -\beta y \end{cases} \)

这里，\(x\)、\(y\)、\(z\)是无量纲的状态变量，\(\alpha\)和\(\beta\)是与电路元件参数相关的无量纲参数，它们就像是电路的 “基因密码”，决定了电路的混沌特性。而\(f(x)\)同样是一个非线性函数，与之前的\(g(u_{C1})\)相对应，在无量纲的世界里继续发挥着它的关键作用。

从实际的电路到抽象的数学方程，这个转化过程是我们理解 Chua 混沌电路的关键一步。它让我们能够运用数学这一强大的工具，对电路的行为进行精确的描述和深入的分析。通过求解这些微分方程，我们可以得到电路在不同时刻的状态，预测电路的混沌行为，为后续的参数估计工作提供了坚实的理论基础。

固定时间自适应参数估计算法实现：关键步骤详解

算法推导过程

基于 Volterra 积分算子推导固定时间自适应参数估计算法，是一个充满挑战但又极具创造性的过程，每一步都蕴含着深刻的数学原理和逻辑。

我们从 Chua 混沌电路的无量纲化数学模型出发，这是我们整个推导的基础。该模型由以下方程组描述：\( \begin{cases} \frac{dx}{dt} = \alpha(y - x - f(x)) \\ \frac{dy}{dt} = x - y + z \\ \frac{dz}{dt} = -\beta y \end{cases} \)

为了实现固定时间自适应参数估计，我们首先对系统方程进行 Volterra 积分算子的映射。这一步的目的是通过积分运算，将方程中的未知量进行巧妙的转化，从而为后续的参数估计创造条件。

对于 Volterra 积分算子\(V_k\)，它对函数\(f(t)\)的映射定义为\([V_kf](t) = \int_{a}^{t}k(t,\tau)f(\tau)d\tau\)，其中核函数\(k(t,\tau)\)的选择至关重要。我们精心选取满足特定条件的核函数，即当\(\tau = 0\)和\(\tau = t\)时，核函数及其导数为零，这样的选择能够有效消除系统初始值的影响，同时避免对系统输出导数的计算。

对系统方程两边同时进行积分算子\(V_k\)运算，得到新的方程。在这个过程中，我们会遇到一些未知量，比如\(y_1\)，\(y_2\)，\(y_3\)的导数是未知的。为了消去这些未知量，我们利用 Volterra 积分算子的性质，将\([V_kf^{(i)}](t)\)展开成关于核函数\(k(t,\tau)\)导数的表达式，然后代入方程中。经过一系列复杂而严谨的数学推导，最终得到一个除了待估计参数\(\alpha\)和\(\beta\)外，其他变量均已知的方程。

有了这个方程后，我们就可以设计观测器来对参数进行精确估计。观测器的设计是基于 Lyapunov 稳定性理论，通过构造合适的 Lyapunov 函数，分析其导数的性质，来确保观测器的稳定性和收敛性。我们定义观测器的状态变量，并建立其与原系统状态变量之间的关系，然后根据得到的方程设计观测器的更新律，使得观测器能够在固定时间内收敛到真实的参数值。

整个推导过程就像是一场精密的数学舞蹈，每一个步骤都紧密相连，每一次数学变换都有着明确的目的和依据。从系统方程的积分算子映射，到未知量的消去，再到观测器的设计，每一步都凝聚着研究者的智慧和努力，为我们实现 Chua 混沌电路的固定时间自适应参数估计奠定了坚实的理论基础。

算法关键参数与设置

在基于 Volterra 积分算子的固定时间自适应参数估计算法中，有几个关键参数对算法的性能起着决定性的作用。

首先是核函数\(k(t,\tau)\)中的设计参数，如\(\omega\)和\(h\)。这些参数就像是核函数的 “调节器”，它们的取值直接影响着核函数的形状和特性，进而影响到 Volterra 积分算子对系统方程的映射效果。当\(\omega\)取值较大时，核函数在积分区间内的变化更加剧烈，这可能会使得积分算子对系统信息的捕捉更加敏感，但同时也可能引入更多的噪声和干扰；而当\(\omega\)取值较小时，核函数的变化相对平缓，积分算子对系统信息的处理更加平滑，但可能会损失一些细节信息。\(h\)参数同样重要，它控制着核函数在\(\tau = 0\)和\(\tau = t\)附近的行为，对消除系统初始值的影响起着关键作用。通过合理调整\(h\)的值，可以使得核函数在这些关键位置的导数满足为零的条件，从而有效地消除初始值的干扰。

观测器中的相关参数，如观测器增益矩阵\(L\)，也是不容忽视的。观测器增益矩阵\(L\)决定了观测器对系统状态估计的速度和精度。如果\(L\)的取值过大，观测器可能会对测量噪声过于敏感，导致估计结果出现较大的波动，就像一个过于敏感的探测器，容易被外界的干扰所误导；而如果\(L\)的取值过小，观测器的收敛速度会变慢，无法及时准确地估计系统状态，就像一个反应迟钝的观察者，总是慢半拍。

在实际应用中，我们需要根据 Chua 混沌电路的具体特性和实际需求来合理设置这些参数。通常可以采用试错法，先根据经验设定一组初始参数值，然后通过仿真实验来观察算法的性能表现。如果算法的收敛速度不理想，我们可以适当调整核函数参数或观测器增益矩阵，再次进行仿真，直到找到一组能够使算法在固定时间内准确收敛的参数值。

也可以结合一些优化算法，如遗传算法、粒子群优化算法等，来自动搜索最优的参数组合。这些优化算法能够在参数空间中进行高效的搜索，快速找到使算法性能最优的参数值，大大提高了参数设置的效率和准确性。

仿真验证：算法效果的直观呈现

仿真实验设置

为了全面而深入地验证基于 Volterra 积分算子的固定时间自适应参数估计算法在 Chua 混沌电路中的性能，我们精心设计并开展了一系列仿真实验。在这个数字化的实验室里，我们选用了功能强大的 Matlab 软件作为实验平台，它就像是一个万能的实验工作台，为我们提供了丰富的工具和函数，使得复杂的数值计算和图形绘制变得轻而易举。

在实验中，我们对 Chua 混沌电路的参数进行了精确的设定。电路中的电容\(C_1 = 10nF\)，\(C_2 = 100nF\)，电感\(L = 18mH\)，电阻\(R = 1000\Omega\)，这些参数的选择并非随意为之，而是基于对 Chua 混沌电路典型特性的深入研究，它们共同构建起了一个标准的 Chua 混沌电路模型。

初始条件的设定同样至关重要，因为混沌系统对初始条件极为敏感，微小的差异都可能导致截然不同的结果。我们将电容\(C_1\)两端的电压初始值\(u_{C1}(0)\)设为\(0.1V\)，电容\(C_2\)两端的电压初始值\(u_{C2}(0)\)设为\(0V\)，电感电流初始值\(i_{L}(0)\)设为\(0A\) 。

对于基于 Volterra 积分算子的固定时间自适应参数估计算法，我们也仔细确定了其中的关键参数。核函数\(k(t,\tau)\)中的设计参数\(\omega = 10\)，\(h = 0.1\)，这组参数的取值是经过多次试验和优化得到的，它们能够使核函数在满足特定条件的同时，充分发挥 Volterra 积分算子的优势。观测器增益矩阵\(L\)的取值则根据 Lyapunov 稳定性理论进行设计，以确保观测器能够快速、准确地收敛到真实的参数值。

结果分析

当我们按下仿真开始的按钮，一场数据的盛宴便在 Matlab 的虚拟世界中展开。随着时间的推移，算法开始对 Chua 混沌电路的参数进行估计，一个个数据点不断生成，逐渐描绘出参数估计值随时间变化的轨迹。

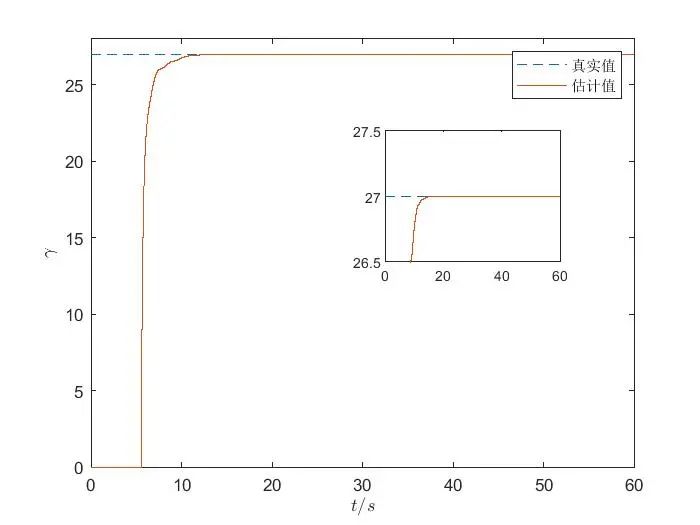
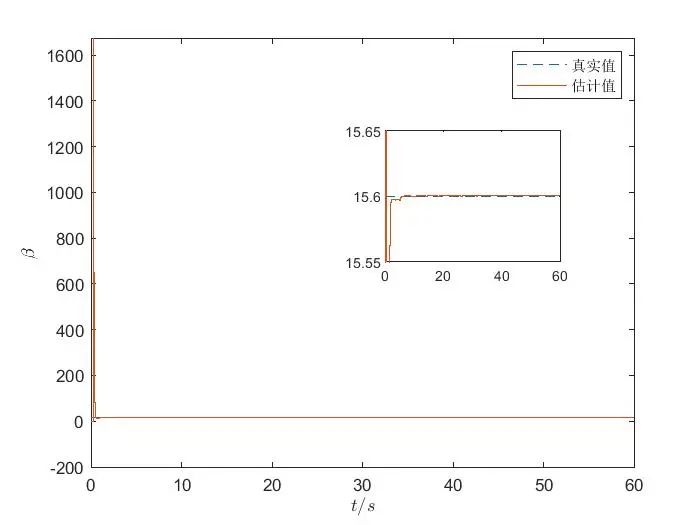
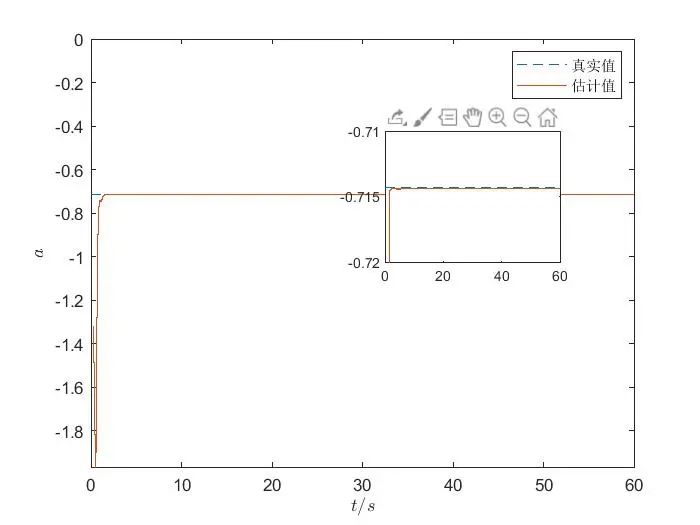
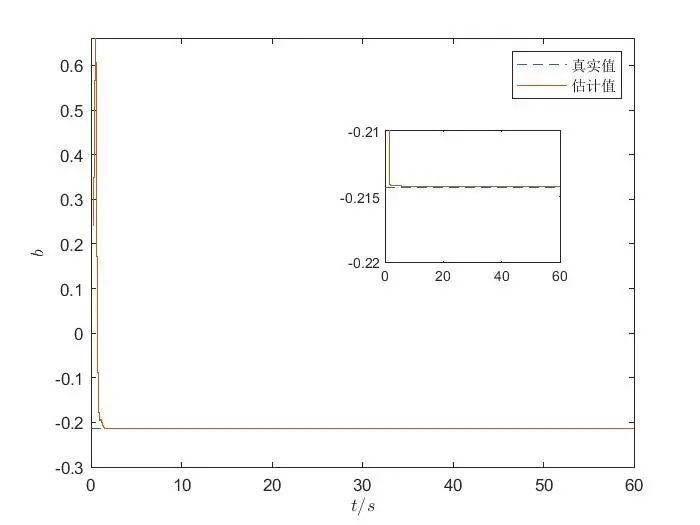
从仿真结果中，我们首先得到了参数估计值随时间变化的曲线。在这条曲线上，我们可以清晰地看到，随着时间的推进，参数\(\alpha\)和\(\beta\)的估计值迅速向其真实值逼近。在最初的阶段，估计值可能会因为算法的初始化和系统的复杂性而出现一定的波动，但很快就会稳定下来，以极快的速度收敛到真实值。这就像是一位精准的射手，虽然在瞄准的初期可能会有一些偏差，但很快就能调整状态，准确命中目标。

为了更直观地评估算法的准确性，我们还绘制了估计误差随时间变化的曲线。这条曲线展示了估计值与真实值之间的误差随着时间的演变情况。从曲线中可以看出，误差在极短的时间内就迅速减小，并在固定时间内收敛到一个极小的值，几乎可以忽略不计。这表明我们的算法具有极高的精度，能够在短时间内准确地估计出 Chua 混沌电路的参数。

为了进一步突出基于 Volterra 积分算子的固定时间自适应参数估计算法的优势，我们将其与其他常见的参数估计算法进行了对比。在对比实验中，我们选取了传统的最小二乘法和基于粒子群优化的参数估计算法。这两种算法在参数估计领域都有着广泛的应用，但在面对 Chua 混沌电路这样复杂的系统时，却暴露出了一些不足。

最小二乘法虽然原理简单，但在收敛速度上明显较慢，需要较长的时间才能使估计值接近真实值，而且在噪声环境下，其估计误差较大，稳定性较差。基于粒子群优化的参数估计算法虽然在一定程度上提高了收敛速度，但由于其本质是一种启发式搜索算法，收敛结果容易受到初始种群和参数设置的影响，导致结果的不确定性较大。

而我们提出的基于 Volterra 积分算子的固定时间自适应参数估计算法，在收敛速度和准确性方面都表现出了显著的优势。它能够在固定时间内快速收敛到真实值，且不受初始条件的影响，无论初始误差大小如何，都能稳定地完成参数估计任务。这种稳定性和高效性，使得它在 Chua 混沌电路的参数估计中具有明显的竞争力，为混沌电路的研究和应用提供了更为可靠的参数估计方法。

总结与展望：探索的延续

通过本次深入研究，我们成功地将基于 Volterra 积分算子的固定时间自适应参数估计算法应用于 Chua 混沌电路，取得了一系列令人瞩目的成果。

在算法优势方面，该算法展现出了卓越的性能。其固定时间收敛的特性，使得参数估计能够在极短的时间内完成，大大提高了估计效率，这对于那些对实时性要求极高的应用场景，如高速通信中的混沌加密和解密过程，具有重要的意义。与传统的参数估计算法相比，它摆脱了对初始条件的依赖，无论初始误差大小如何，都能稳定、可靠地收敛到真实参数值，就像是一位训练有素的运动员，无论起跑状态如何，都能坚定地冲向终点，这种稳定性和可靠性在实际工程应用中是至关重要的。

从实际应用价值来看，我们的研究成果为 Chua 混沌电路在众多领域的进一步应用奠定了坚实的基础。在通信领域，准确的参数估计可以增强混沌加密的安全性，为信息的传输提供更可靠的保障，让我们的通信内容在复杂的网络环境中得到更好的保护。在混沌控制领域，精确的参数了解是实现有效控制的前提，通过我们的算法准确估计参数后，能够更加精准地调控混沌电路的行为，使其满足各种实际需求，就像一位熟练的驾驶员，能够精准地操控汽车，驶向我们期望的方向。

然而，我们也清醒地认识到，任何研究都不是完美无缺的，本次研究同样存在一定的局限性。在实际电路中，不可避免地会存在各种噪声和干扰，虽然我们的算法在一定程度上具有抗干扰能力，但当噪声强度过大时，仍然可能对参数估计的准确性产生影响。算法的计算复杂度相对较高，这在一些资源受限的设备上应用时，可能会面临挑战，就像一辆高性能的跑车，虽然速度很快，但对燃料和道路条件的要求也很高。=