1 算法介绍
1.1引言
复杂科学
- 20世纪80年代,以美国圣塔菲(SantaFe)学派为首提出了复杂科学,一经提出,在世界范围内引起了广泛的关注。目前,关于复杂性和复杂系统的科学研究占据着越来越重要的位置,以至于被有些科学家誉为“21世纪的科学”。
- 1985年,耗散结构理论的创始人,诺贝尔化学奖获得者I.Prigogine提出了社会经济复杂系统中的自组织问题。1988年,诺贝尔物理学奖获得者P.Anderson和诺贝尔经济学奖获得者K.J.Arow通过组织专题讨论会,提出了经济管理可以看作是一个演化着的复杂系统。此后,随着研究的不断深入,复杂系统中所涉及的非线性、非平衡、突变、混沌、分形、自组织等理论在经济管理领域有了越来越广泛的应用。
元胞自动机
- 在复杂性和复杂系统的研究过程中,国内外学者提出了许多探索复杂性的方法及工具,其中,元胞自动机(cellularautomaton,CA)以其组成单元的简单规则性,单元之间作用的局部性和信息处理的高度并行性,并表现出复杂的全局性等特点而备受关注,成为探索复杂系统的一种有效工具。
2元胞自动机的基本理论及方法
2.1元胞自动机的发展
- 20世纪50年代初,现代计算机的创始人冯·诺依曼(vonNeuman)为模拟生物发育中细胞的自我复制而提出了元胞自动机的雏形。但在当时这项工作并未引起广泛的关注与重视。
- 1970年,剑桥大学的J.H.Conway设计了一种计算机游戏———“生命的游戏”。它是具有产生动态图案和动态结构能力的元胞自动机模型,吸引了众多科学家的兴趣,推动了元胞自动机研究的迅速发展。
- 之后,S.Wolfram对初等元胞自动机的256种规则产生的所有模型进行了详细而深入的研究。他还用熵来描述其演化行为,把元胞自动机分为:平稳型、周期型、混沌型、复杂型四类。
- 近年来随着复杂性研究的进展,作为探索复杂系统的一种有效工具,元胞自动机获得了深入的研究和广泛的应用。
2.2元胞自动机的构成特征
2.2.1元胞自动机的构成
标准元胞自动机是一个由「元胞、元胞状态、邻域和状态更新规则」构成的四元组,用数学符号可以表示为A=(L,d,S,N,f)
- A代表一个元胞自动机系统
- L表示元胞空间
- d表示元胞自动机内元胞空间的维数,是一正整数
- S是元胞有限的、离散的状态集合
- N表示某个邻域内所有元胞的集合
- f表示局部映射或局部规则。
具体描述:
- 元胞空间
- 元胞是构成元胞自动机的最基本单元,而元胞空间是元胞所分布的空间网点集合。
- 理论上,元胞空间是在各维向上无限延展的,但实际中无法在计算机上实现。因此,需要定义不同的边界条件。
- 元胞空间的边界条件主要有三种类型:周期型、反射型和定值型。
- 元胞状态
- 通常在某一个时刻一个元胞只能有一种元胞状态,而且该状态取自一个有限集合,如{0,1},{生,死}或{0,a1,a2,an}。
- 在社会科学领域中,元胞状态可以用来代表个体所持的态度、个体特征或行为等。
- 邻域
- 在空间位置上与元胞相邻的细胞称为它的邻元,由所有邻元组成的区域称为它的邻域。
- 在一维元胞自动机中,通常以半径r来确定邻域,距离某个元胞r内的所有元胞均被认为是该元胞的邻域。
- 一维元胞自动机的邻域:
-



- 在二维元胞自动机中,通常有以下几种类型的邻域:
- 冯·诺依曼型(vonNeumanNeighborhoods)
- 摩尔型(MooreNeighborhoods)
- 马哥勒斯型(MargolusNeighborhoods)
- 它是每次将一个2×2的元胞块做统一处理,而上述前两类邻域中,每个元胞是分别处理的
-



- 同样,也可以定义二维以上的高维元胞自动机的邻域
- 状态更新规则
- 是指根据元胞当前状态及其邻域中元胞的状态决定下一时刻该元胞状态的状态转移函数。
- 状态更新规则可以写为
,

 为t时刻的邻域状态组合,称为元胞自动机的局部映射或局部规则。
为t时刻的邻域状态组合,称为元胞自动机的局部映射或局部规则。

2.2.2标准元胞自动机的特征
- 离散性:元胞自动机的空间、时间及状态都是离散的。
- 同质性:元胞空间中每个单元格可能具有的状态集合相同,并且决定各个元胞状态变化的规则也是相同的。
- 并行性:元胞空间中各个元胞按状态更新规则变化是同步进行的,特别适合于并行计算,且各个元胞的状态变化是独立行为,互相没有任何影响。
- 局部性:一个元胞在t+1时刻的状态由其周围半径为r的邻域中的元胞的当前时刻t的状态决定,因此,在时间、空间上都存在着局部性。
- 维数高:元胞自动机是一类无穷维动力系统。
1.3元胞自动机在管理系统中的应用
元胞自动机已被广泛地应用于社会、经济、军事以及自然科学的各个领域
- 在社会学中,元胞自动机用于研究政治组织的突现、个人行为的社会性、流言的传播等。
- 在生物学中,用于肿瘤细胞的增长机理和过程模拟、人类大脑的机理探索、艾滋病病毒HIV的感染过程、自组织、自繁殖等生命现象的研究以及克隆技术的研究。
- 在计算机科学中,元胞自动机被视为并行计算机而用于并行计算的研究。
- 在物理学中,除了格子气元胞自动机在流体力学上的成功应用,元胞自动机还应用于磁场、电场等场的模拟,以及热扩散、热传导和机械波的模拟。
- 在军事科学中,元胞自动机用于模拟军事作战,理解战争过程。
- 在管理领域,国内外学者开始应用元胞自动机来解释分析各种管理现象,对各种管理现象进行演化模拟。
元胞自动机在管理系统中的应用:


2 部分代码
3 仿真结果
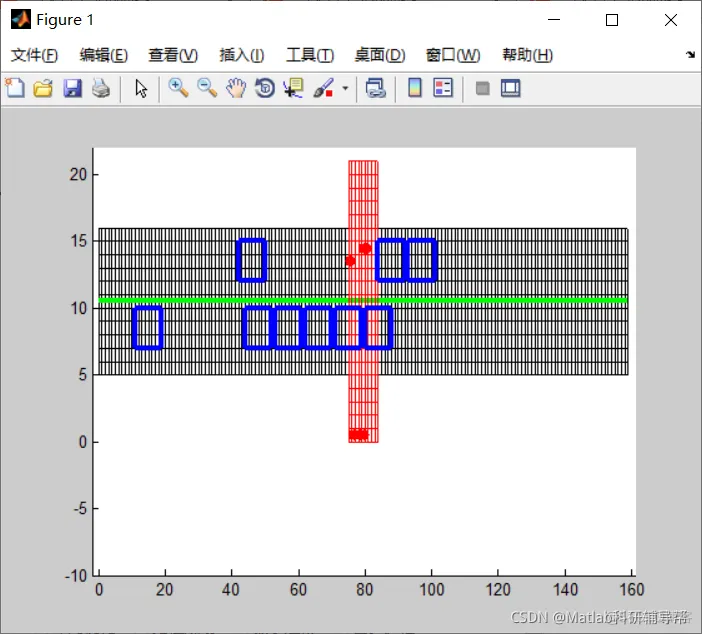


4 参考文献
[1]薛逻维. 基于元胞自动机的公交车内行人流仿真及其应用[D].华东交通大学,2020.
5 代码下载





















 780
780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








