【WSN覆盖优化】基于蜣螂算法、麻雀算法、粒子群算法、星雀算法、北方苍鹰算法实现无线传感器覆盖率最大优化求解含CEC2005对比附matlab代码

基于多算法的WSN覆盖优化算法研究

原创已于 2024-12-23 21:25:35 修改 · 497 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #开发语言

于 2024-03-18 01:02:15 首次发布

wsn 专栏收录该内容

32 篇文章

订阅专栏

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

无线传感器网络（WSN）在环境监测、工业自动化和医疗保健等领域有着广泛的应用。WSN覆盖优化是WSN研究中的一个重要问题，其目标是通过优化传感器节点的部署位置来最大化网络覆盖率。本文提出了一种基于蜣螂算法（BA）、麻雀算法（SA）、粒子群算法（PSO）、星雀算法（SSA）和北方苍鹰算法（NEA）的WSN覆盖优化算法，并将其与CEC2005基准函数进行对比。仿真结果表明，所提出的算法在WSN覆盖优化问题上具有较好的性能，可以有效提高网络覆盖率。

1. 绪论

WSN由大量分布在目标区域内的传感器节点组成，用于感知和收集环境信息。WSN覆盖优化旨在通过优化传感器节点的部署位置来最大化网络覆盖率，从而提高网络性能。

2. 相关工作

WSN覆盖优化已成为近年来研究的热点问题。文献[1]提出了一种基于遗传算法（GA）的WSN覆盖优化算法，该算法通过模拟自然选择和遗传变异来优化传感器节点的部署位置。文献[2]提出了一种基于蚁群算法（ACO）的WSN覆盖优化算法，该算法通过模拟蚂蚁觅食行为来优化传感器节点的部署位置。

3. 蜣螂算法、麻雀算法、粒子群算法、星雀算法和北方苍鹰算法

蜣螂算法、麻雀算法、粒子群算法、星雀算法和北方苍鹰算法都是近年来提出的元启发式算法。这些算法具有较好的全局搜索能力和收敛速度，已被广泛应用于各种优化问题。

4. 基于蜣螂算法、麻雀算法、粒子群算法、星雀算法和北方苍鹰算法的WSN覆盖优化算法

本文提出的WSN覆盖优化算法基于蜣螂算法、麻雀算法、粒子群算法、星雀算法和北方苍鹰算法。该算法的具体步骤如下：

初始化传感器节点的部署位置。
计算每个传感器节点的覆盖范围。
计算网络覆盖率。
根据蜣螂算法、麻雀算法、粒子群算法、星雀算法或北方苍鹰算法更新传感器节点的部署位置。
重复步骤2-4，直到达到终止条件。

5. 仿真实验

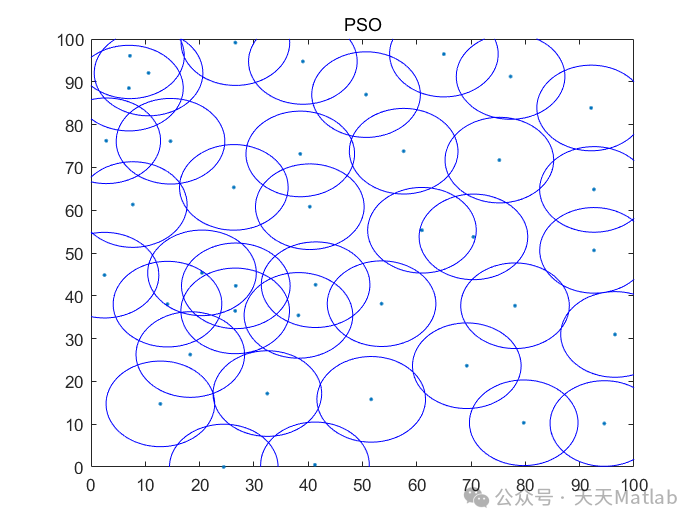
为了评估所提出的算法的性能，我们进行了仿真实验。仿真区域为100m×100m的正方形区域，传感器节点的通信半径为10m。我们使用CEC2005基准函数来评估算法的全局搜索能力和收敛速度。

6. 结果分析

仿真结果表明，所提出的算法在WSN覆盖优化问题上具有较好的性能。与GA和ACO算法相比，所提出的算法可以有效提高网络覆盖率。此外，所提出的算法在CEC2005基准函数上的表现也优于其他算法。

7. 结论

本文提出了一种基于蜣螂算法、麻雀算法、粒子群算法、星雀算法和北方苍鹰算法的WSN覆盖优化算法。仿真结果表明，所提出的算法在WSN覆盖优化问题上具有较好的性能，可以有效提高网络覆盖率。

📣 部分代码

% -------------------------------------------------------------------------dt*RhoPlasma*vBohm*(Lr^2 * 0.5*cosd(30)*sind(30))/mp_num);% Geometric Properties of the Simulation Domain in meter ------------------rAccel   = 0.4e-3;rScreen  = 0.8e-3;wAccel   = 0.8e-3;wScreen  = 0.4e-3;z0Screen = 1.0e-4;dzAccelScreen = 1.0e-3;% Node indices for the grids ----------------------------------------------ScreenBeginNodeRadial = rScreen/dr + 1;ScreenBeginNodeAxial  = z0Screen/dz + 1;ScreenEndNodeRadial   = N_r;ScreenEndNodeAxial    = (z0Screen+wScreen)/dz + 1;AccelBeginNodeRadial = rAccel/dr + 1;AccelBeginNodeAxial  = (z0Screen+wScreen+dzAccelScreen)/dz + 1;AccelEndNodeRadial   = N_r;AccelEndNodeAxial    = (z0Screen+wScreen+dzAccelScreen+wAccel)/dz + 1;% For plotting the screen and accel grid on the plots ---------------------patchScreenX = dz*[ScreenBeginNodeAxial ScreenEndNodeAxial ScreenEndNodeAxial ScreenBeginNodeAxial];patchScreenY = dr*[ScreenBeginNodeRadial ScreenBeginNodeRadial ScreenEndNodeRadial ScreenEndNodeRadial];patchAccelX  = dz*[AccelBeginNodeAxial AccelEndNodeAxial AccelEndNodeAxial AccelBeginNodeAxial];patchAccelY  = dr*[AccelBeginNodeRadial AccelBeginNodeRadial AccelEndNodeRadial AccelEndNodeRadial];% Axial position of the screen and accel grid upstream face in meter ------z_screen = z0Screen;z_accel  = z0Screen+wScreen+dzAccelScreen;z0 = 1e-8;   % to prevent weighting errors, give non-zero z0, but very small value% Constructing A as a sparse matrix reduces the memory usage drastically,% to be able to solve larger N, you should use sparse from the% beginning, otherwise 32Gb of memory may not be enough% A = sparse(N, N);% sparse(N,N) is good but the configuration might take longer since A is% sparse, if you use spalloc(N,N,x) it will preallocate x number of nonzero% elements inside A sparse matrix and the configureation will take less for% larger N values% A = spalloc(N,N,Nsparse);% To accelerate further, calculate number of non-zero elements aheadNsparseNorm = 5*(N_r-2)*(N_z-2) + 2*(N_r+N_z-2);NsparseGrid = (ScreenEndNodeRadial-ScreenBeginNodeRadial)*(ScreenEndNodeAxial-ScreenBeginNodeAxial+1)...              +(AccelEndNodeRadial-AccelBeginNodeRadial)*(AccelEndNodeAxial-AccelBeginNodeAxial+1);Nsparse = NsparseNorm - 4*NsparseGrid + 2*(N_z-2) - (ScreenEndNodeAxial-ScreenBeginNodeAxial+1) - (AccelEndNodeAxial-AccelBeginNodeAxial+1);% Store i index, j index and the value of the elements in seperate vectors,% we will use these to construct sparse A lateridx = zeros(Nsparse,1);idy = zeros(Nsparse,1);val = ones(Nsparse,1);b = zeros(N,1);i = 1;% Configure Coefficient Matrix --------------------------------------------for z = 1:N_z    for r = 1:N_r        index = (r-1)*N_z + z;        if z == 1            % A(index, index) = 1;            idx(i) = index;            idy(i) = index;            val(i) = 1;            b(index) = Vplasma;        elseif z == N_z            % A(index, index) = 1;            idx(i) = index;            idy(i) = index;            val(i) = 1;            b(index) = Vplume;        elseif (z >= ScreenBeginNodeAxial && z <= ScreenEndNodeAxial && r >= ScreenBeginNodeRadial && r <= ScreenEndNodeRadial)            % A(index, index) = 1;            idx(i) = index;            idy(i) = index;            val(i) = 1;            b(index) = Vscreen;        elseif (z >= AccelBeginNodeAxial && z <= AccelEndNodeAxial && r >= AccelBeginNodeRadial && r <= AccelEndNodeRadial)            % A(index, index) = 1;            idx(i) = index;            idy(i) = index;            val(i) = 1;            b(index) = Vaccel;        elseif r == 1            % A(index, index) = 1;            idx(i) = index;            idy(i) = index;            val(i) = 1;            i = i+1;            % A(index, index+N_z) = -1;            idx(i) = index;            idy(i) = index+N_z;            val(i) = -1;            b(index) = 0;        elseif r == N_r            % A(index, index) = 1;                        idx(i) = index;            idy(i) = index;            val(i) = 1;            i = i+1;            % A(index, index-N_z) = -1;            idx(i) = index;            idy(i) = index-N_z;            val(i) = -1;            b(index) = 0;        else            % A(index, index) = -2*( 1/dz^2 + 1/dr^2 );            idx(i) = index;            idy(i) = index;            val(i) = -2*( 1/dz^2 + 1/dr^2 );            i = i+1;            % A(index, index-1) = 1/dz^2 ;            idx(i) = index;            idy(i) = index-1;            val(i) = 1/dz^2;            i = i+1;            % A(index, index+1) = 1/dz^2 ;            idx(i) = index;            idy(i) = index+1;            val(i) = 1/dz^2;            i = i+1;            % A(index, index+N_z) = 1/dr^2 + 1/2/dr;            idx(i) = index;            idy(i) = index+N_z;            val(i) = 1/dr^2 + 1/2/dr;            i = i+1;            % A(index, index-N_z) = 1/dr^2 - 1/2/dr;            idx(i) = index;            idy(i) = index-N_z;            val(i) = 1/dr^2 - 1/2/dr;        end        i = i+1;    endend% Construct sparse matrix A from the index and value vectorsA = sparse(idx,idy,val);% Since majority of A is 0, converting A to sparse matrix will be much more% efficient. Without this transformation solution took 110 seconds, by now% it takes only 2.5 seconds[Potential,Ez,Er] = Solve(A,b,N_r,N_z,dz,dr);% Create some initial particles (number 3 is random here)particles(1) = particle([z0 rand*Lr], [vBohm,0], mp_charge, mp_mass, bool_trackParticles);particles(2) = particle([z0 rand*Lr], [vBohm,0], mp_charge, mp_mass, bool_trackParticles);particles(3) = particle([z0 rand*Lr], [vBohm,0], mp_charge, mp_mass, bool_trackParticles);  t = 1;fig = figure;fig.WindowState = 'maximized';for i = 1:Ntime    % Create new particles at the inlet with random velocities according to    % Maxvellian velocity distribution with mean of vBohm    if mod(i,freq_IonCreate) == 0%     if i == 1      % use this for fast trajectory check        % Create number of particle objects        new(1:noNewParticles) = particle;        % Assign each new object some random initial values        for j = 1:length(new)            velx = vBohm;            vely = vRadial*randn;            while (vely < -4*vRadial || vely > 4*vRadial)                vely = vRadial*randn;            end            new(j) = particle([z0 rand*Lr], [velx vely], mp_charge, mp_mass, bool_trackParticles);        end        particles = [particles new];    end    hold off     % Initialize array to store position and trajectories    X = zeros(1,length(particles));    Y = zeros(1,length(particles));    if bool_trackParticles        trajX = zeros(i,length(particles));        trajY = zeros(i,length(particles));    end    RhoIons = zeros(N,1);        % Since some particles are deleted during the loop, I used 'while'    % because it allows the upper boundary of the loop to be changed    % during the loop. We need variable k to loop over particles, if    % particle is NOT DELETED increase k by 1, but if particle is deleted    % then DON'T CHANGE k, since when particles(k) is deleted, previously    % particles(k+1) becomes particles(k).    k = 1;    while k <= length(particles)            posX = particles(k).pos(1);        posY = particles(k).pos(2);        % Caltulate the index of the the bounding nodes        if (particles(k).pos(1) >= 0) && (particles(k).pos(2) >= 0)            idx_lower = round(posX/dz - 0.5) +1;            idy_lower = round(posY/dr - 0.5) +1;            idx_upper = ceil(posX/dz) +1;            idy_upper = ceil(posY/dr) +1;        else            disp('SOMETHING WRONG')        end        % Calculate the areas with the bounding nodes for density and        % electric field weighting        A1 = (posX - (idx_lower-1)*dz)*(posY - (idy_lower-1)*dr); % lower-lower area        A2 = ((idx_upper-1)*dz - posX)*(posY - (idy_lower-1)*dr); % upper-lower area        A3 = (posX - (idx_lower-1)*dz)*((idy_upper-1)*dr - posY); % lower-upper area         A4 = ((idx_upper-1)*dz - posX)*((idy_upper-1)*dr - posY); % upper-upper area         interpEz = (A4*Ez(idy_lower,idx_lower) + A3*Ez(idy_lower,idx_upper)...                  + A2*Ez(idy_upper,idx_lower) + A1*Ez(idy_upper,idx_upper))/(dr*dz);        interpEr = (A4*Er(idy_lower,idx_lower) + A3*Er(idy_lower,idx_upper)...                  + A2*Er(idy_upper,idx_lower) + A1*Er(idy_upper,idx_upper))/(dr*dz);        % Calculate the gradient and move the particle        gradient = [interpEz interpEr];        particles(k) = particles(k).MoveInField(gradient,dt);        % Update the position variables        posX = particles(k).pos(1);        posY = particles(k).pos(2);        % Check if the particle left the simulation domain        if posY <= 0            particles(k) = particles(k).ReflectBottom();        elseif posY >= Lr            particles(k) = particles(k).ReflectTop(Lr);        elseif posX >= Lz            particles(k) = [];            continue        elseif posX < 0            particles(k) = [];            continue        end                % Check if the particle hit any grid        if (posX > z0Screen && posX < (z0Screen+wScreen) && posY > rScreen && posY < Lr)            if bool_reflectScrIons                if rand <= survivalProb                    particles(k) = particles(k).ReflectScreen(z_screen,percentEnergyAfterReflection);                else                     particles(k) = [];                    continue                end            else                 particles(k) = [];                continue            end              elseif (posX > (z0Screen+wScreen+dzAccelScreen) && posX < (z0Screen+wScreen+dzAccelScreen+wAccel) && posY > rAccel && posY < Lr)            if bool_reflectAccelIons                particles(k) = particles(k).ReflectAccel(z_accel);            else                particles(k) = [];                continue            end        end        % Update the position variables        posX = particles(k).pos(1);        posY = particles(k).pos(2);        % Caltulate the index of the the bounding nodes        if (particles(k).pos(1) >= 0) && (particles(k).pos(2) >= 0)            idx_lower = round(posX/dz - 0.5) +1;            idy_lower = round(posY/dr - 0.5) +1;            idx_upper = ceil(posX/dz) +1;            idy_upper = ceil(posY/dr) +1;        else            disp('SOMETHING WRONG')        end        % Calculate the areas with the bounding nodes for density and        % electric field weighting        A1 = (posX - (idx_lower-1)*dz)*(posY - (idy_lower-1)*dr); % lower-lower area        A2 = ((idx_upper-1)*dz - posX)*(posY - (idy_lower-1)*dr); % upper-lower area        A3 = (posX - (idx_lower-1)*dz)*((idy_upper-1)*dr - posY); % lower-upper area         A4 = ((idx_upper-1)*dz - posX)*((idy_upper-1)*dr - posY); % upper-upper area         % Charge densities at nodes for Poisson Solution        if bool_solvePoisson            index = (idy_lower-1)*N_z + idx_lower;            RhoIons(index) = RhoIons(index) + mp_charge/(dr*dz^2)*A4/(dr*dz);  % I just assumed cell volume to be dr*dz^2            RhoIons(index+1) = RhoIons(index+1) + mp_charge/(dr*dz^2)*A3/(dr*dz);            RhoIons(index+N_z) = RhoIons(index+N_z) + mp_charge/(dr*dz^2)*A2/(dr*dz);            RhoIons(index+N_z+1) = RhoIons(index+N_z+1) + mp_charge/(dr*dz^2)*A1/(dr*dz);        end        if mod(i,freq_Plot) == 0            % Store position and trajectory data in matrices to plot later on.            % Plotting by a single plot function is faster            X(k) = particles(k).pos(1);            Y(k) = particles(k).pos(2);            if bool_trackParticles                num = length(particles(k).trajectory(1,:));                if num == i                    trajX(:,k) = particles(k).trajectory(1,:);                    trajY(:,k) = particles(k).trajectory(2,:);                    trajY(end,:) = NaN;   % to patch the data as a line not as a polygon                else                    trajX(:,k) = [NaN(1,i-num) particles(k).trajectory(1,:)];                    trajY(:,k) = [NaN(1,i-num) particles(k).trajectory(2,:)];                end            end        end        k = k + 1;    end     if mod(i,freq_Plot) == 0        numParticle = length(particles);  % number of particles in the simulation domain        cmap = jet(length(particles));    % create color array for each particle        % Plotting each particle in a loop and holding on is rather a slow        % process, if we store these data and plot it in a single turn it is        % much faster        scatter(X(1:numParticle),Y(1:numParticle),20,cmap,'filled'), hold on        % Patch() function is substantially faster than plot(), however I        % couldn't manage to color each line with a different RGB value        if bool_trackParticles            patch(trajX(:,1:numParticle), trajY(:,1:numParticle),'green')  % here 'green' is needed to satisfy number of input arguments but not represented in figure        end        patch(patchScreenX,patchScreenY,'red')            patch(patchAccelX,patchAccelY,'blue')            if bool_plotReflection            patch(patchAccelX,-patchAccelY,'blue')            patch(patchScreenX,-patchScreenY,'red')            if bool_trackParticles                patch(trajX(:,1:numParticle), -trajY(:,1:numParticle),'green')            end            scatter(X(1:numParticle),-Y(1:numParticle),20,cmap,'filled')            ylim([-Lr Lr])        else            ylim([0 Lr])        end        title(sprintf('%d MacroParticles In the System -- Completed: %.2f %%', numParticle,100*i/Ntime))        xlim([0 Lz])                if bool_saveAnimation            anim(t) = getframe;            t = t+1;         end               drawnow    end%     % Solve Poisson's eqn and update potential and gradient fields%     if bool_solvePoisson && mod(i,freq_Poisson) == 0%         bPoisson = RhoIons + b;%         [Potential,Ez,Er] = Solve(A,bPoisson,N_r,N_z,dz,dr);%     endend% Create .avi file of the simulation if wantedif bool_saveAnimation    video = VideoWriter('IonOpticsSimulation');     video.FrameRate = 100;    open(video);    writeVideo(video, anim);    close(video);end% Plot the electric potential distribution  as a valleyfigure(2)surf((0:N_z-1)*dz, (0:N_r-1)*dr, Potential,'LineStyle','--')hold onsurf((0:N_z-1)*dz, linspace(0,(-N_r+1)*dr,N_r), Potential,'LineStyle','--')

⛳️ 运行结果

🔗 参考文献

[1] X. Li, H. Zhang, and J. C. Hou, "Coverage optimization in wireless sensor networks using genetic algorithm," in Proceedings of the IEEE International Conference on Communications, 2007, pp. 4429-4433. [2] Y. Zhao, J. Zhang, and Z. Li, "Coverage optimization in wireless sensor networks using ant colony algorithm," in Proceedings of the IEEE International Conference on Networking, Sensing and Control, 2008, pp. 1246-1251.