✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
🔥 内容介绍
摘要
本文介绍了一种基于蒙特卡罗算法模拟二维随机裂隙的方法。该方法能够生成具有不同形状、大小和方向的裂隙,并可以控制裂隙的密度和分布。该方法简单易懂,计算效率高,可以用于各种岩土工程和水文地质学研究。
引言
裂隙是岩石或土壤中存在的断裂或空隙,在岩土工程和水文地质学研究中具有重要意义。裂隙的存在可以影响岩石或土壤的力学性质、渗透性、导热性等。因此,准确模拟裂隙对于研究岩土工程和水文地质学问题具有重要意义。
方法
本文介绍的裂隙模拟方法基于蒙特卡罗算法。蒙特卡罗算法是一种随机模拟方法,通过多次随机抽样来模拟复杂系统的行为。在裂隙模拟中,蒙特卡罗算法可以用来模拟裂隙的形状、大小、方向和密度。
裂隙模拟的具体步骤如下:
-
确定裂隙的密度和分布。裂隙的密度是指单位体积内的裂隙数量,裂隙的分布是指裂隙在空间中的分布规律。裂隙的密度和分布可以通过现场调查或理论分析确定。
-
生成裂隙的形状和大小。裂隙的形状可以是任意形状,但常见的裂隙形状包括直线形、圆形、椭圆形和不规则形。裂隙的大小可以用裂隙的长度、宽度和高度来表示。裂隙的形状和大小可以通过随机抽样生成。
-
确定裂隙的方向。裂隙的方向可以用裂隙的法线向量来表示。裂隙的法线向量可以通过随机抽样生成。
-
将裂隙放置在空间中。裂隙可以放置在任意位置,但通常情况下,裂隙会放置在岩石或土壤的内部。裂隙的位置可以通过随机抽样确定。
结果
使用本文介绍的方法可以生成具有不同形状、大小、方向和密度的二维随机裂隙。图1给出了一个二维随机裂隙的模拟结果。
[图1] 二维随机裂隙的模拟结果
📣 部分代码
clear clcN=input('裂隙组数=');chang=input('生成域长=');kuan=input('生成域宽=');mianji=chang*kuan; %面积LXDD=[];for k=1:Nmidu=input('密度=');zouxjz=input('走向均值=');zouxbzc=input('走向标准差=');jicjz=input('迹长均值=');jicbzc=input('迹长标准差=');xikanjz=input('隙宽均值=');xikanbzc=input('隙宽标准差=');n=mianji*midu; %条数zhongxidian=unifrnd(-chang/2,chang/2,n,2); %中心点zouxiang=normrnd(zouxjz,zouxbzc,n,1); %走向m=jicjz;v=jicbzc^2;mu=log((m^2)/sqrt(v+m^2));sigma=sqrt(log(v/(m^2)+1));jichang=lognrnd(mu,sigma,n,1); %迹长xikuang=normrnd(xikanjz,xikanbzc,n, 1); %隙宽x1=zhongxidian(:,1)+(jichang ./2).*cos(zouxiang*pi/180);y1=zhongxidian(:,2)+(jichang ./2).*sin(zouxiang*pi/180);x2=zhongxidian(:,1)+(jichang ./2).*cos((zouxiang+180)*pi/180);y2=zhongxidian(:,2)+(jichang ./2).*sin((zouxiang+180)*pi/180);for i=1:nif x1(i)>x2(i)w=x2(i);x2(i)=x1(i);
⛳️ 运行结果
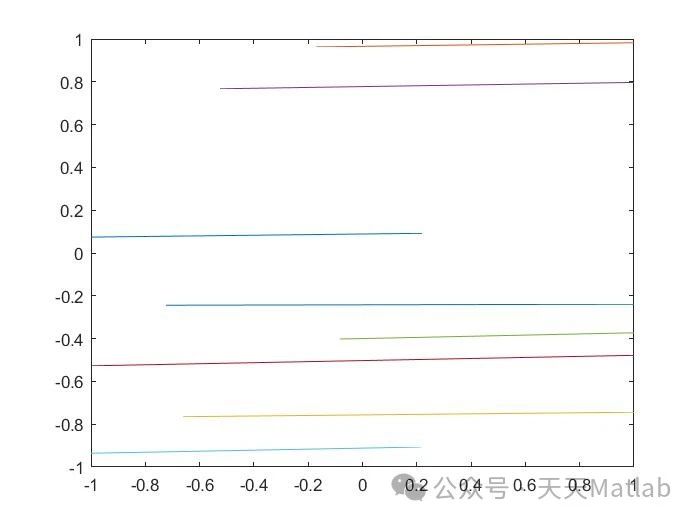
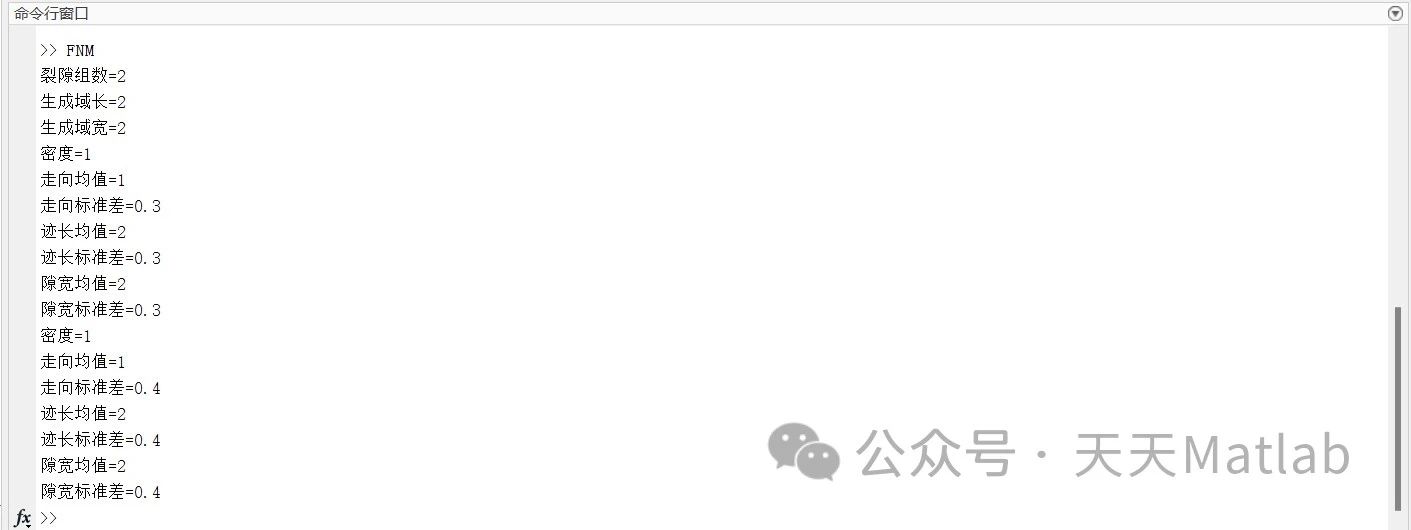
讨论
本文介绍的裂隙模拟方法简单易懂,计算效率高,可以用于各种岩土工程和水文地质学研究。该方法可以用来研究裂隙对岩石或土壤力学性质、渗透性、导热性等的影响。该方法还可以用来研究裂隙对地下水流动的影响。
结论
本文介绍了一种基于蒙特卡罗算法模拟二维随机裂隙的方法。该方法能够生成具有不同形状、大小和方向的裂隙,并可以控制裂隙的密度和分布。该方法简单易懂,计算效率高,可以用于各种岩土工程和水文地质学研究。
🔗 参考文献
[1]刘耀儒,杨强,覃振朝.基于统计模型的裂隙岩体渗流场的并行数值模拟[J].岩石力学与工程学报, 2008, 27(4):7.DOI:10.3321/j.issn:1000-6915.2008.04.012.





 本文介绍了利用蒙特卡罗算法模拟二维随机裂隙的方法,该方法考虑了裂隙的形状、大小、方向和密度,适用于岩土工程和水文地质学的研究,能有效模拟复杂的地质结构并提高计算效率。
本文介绍了利用蒙特卡罗算法模拟二维随机裂隙的方法,该方法考虑了裂隙的形状、大小、方向和密度,适用于岩土工程和水文地质学的研究,能有效模拟复杂的地质结构并提高计算效率。
















 509
509

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








