✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
⛄ 内容介绍
基于反向传播(Backpropagation, BP)神经网络的回归预测是一种常见的机器学习方法,用于预测连续型变量的值。下面将介绍基于BP神经网络的回归预测的基本原理和步骤。
- 数据准备:收集回归预测所需的训练数据,包括输入特征和对应的目标变量(连续型值)。
- 网络结构设计:选择合适的BP神经网络结构,包括输入层、隐藏层和输出层的节点数、层数以及激活函数的选择。网络结构的设计应根据具体问题和数据特点进行调整。
- 数据预处理:对输入特征和目标变量进行预处理,如归一化或标准化处理,以提高网络训练的效果和准确性。
- 网络训练:使用训练数据对BP神经网络进行训练,通过反向传播算法来更新网络参数,使得网络的输出逼近目标变量。
- 网络验证和调整:使用验证数据评估网络的性能,并根据验证结果进行网络结构的调整,如调整隐藏层节点数、增加正则化项等,以提高网络的泛化能力。
- 网络测试:使用测试数据对训练好的BP神经网络进行性能评估,验证其在未知数据上的预测准确性和鲁棒性。
- 结果分析:分析网络输出与目标变量之间的差异,评估网络的预测精度和准确性,并根据需要进行进一步优化或改进。
需要注意的是,BP神经网络的训练过程是一个迭代优化的过程,可能需要多次调整网络参数和结构,并进行多轮训练才能得到较好的预测结果。此外,对于复杂的回归预测问题,可能需要更深层次、更复杂的神经网络结构来提高预测性能。
⛄ 代码
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据
res = xlsread('数据集.xlsx');
%% 划分训练集和测试集
temp = randperm(719);
P_train = res(temp(1: 500), 1 : 28)';
T_train = res(temp(1: 500), 29: 31)';
M = size(P_train, 2);
P_test = res(temp(501: end), 1 : 28)';
T_test = res(temp(501: end), 29: 31)';
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 创建网络
net = newff(p_train, t_train, 10);
%% 设置训练参数
net.trainParam.epochs = 1000; % 迭代次数
net.trainParam.goal = 1e-6; % 误差阈值
net.trainParam.lr = 0.01; % 学习率
net.trainFcn = 'trainlm';
%% 训练网络
net = train(net, p_train, t_train);
%% 仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test );
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
for i = 1: 3
%% 均方根误差
error1(i, :) = sqrt(sum((T_sim1(i, :) - T_train(i, :)).^2) ./ M);
error2(i, :) = sqrt(sum((T_sim2(i, :) - T_test (i, :)).^2) ./ N);
%% 绘图
figure
subplot(2, 1, 1)
plot(1: M, T_train(i, :), 'r-*', 1: M, T_sim1(i, :), 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1(i, :))]};
title(string)
xlim([1, M])
grid
subplot(2, 1, 2)
plot(1: N, T_test(i, :), 'r-*', 1: N, T_sim2(i, :), 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2(i, :))]};
title(string)
xlim([1, N])
grid
%% 分割线
disp('**************************')
disp(['下列是输出', num2str(i)])
disp('**************************')
%% 相关指标计算
% 决定系数 R2
R1(i, :) = 1 - norm(T_train(i, :) - T_sim1(i, :))^2 / norm(T_train(i, :) - mean(T_train(i, :)))^2;
R2(i, :) = 1 - norm(T_test (i, :) - T_sim2(i, :))^2 / norm(T_test (i, :) - mean(T_test (i, :)))^2;
disp(['训练集数据的R2为:', num2str(R1(i, :))])
disp(['测试集数据的R2为:', num2str(R2(i, :))])
% 平均绝对误差 MAE
mae1(i, :) = sum(abs(T_sim1(i, :) - T_train(i, :))) ./ M ;
mae2(i, :) = sum(abs(T_sim2(i, :) - T_test (i, :))) ./ N ;
disp(['训练集数据的MAE为:', num2str(mae1(i, :))])
disp(['测试集数据的MAE为:', num2str(mae2(i, :))])
% 平均相对误差 MBE
mbe1(i, :) = sum(T_sim1(i, :) - T_train(i, :)) ./ M ;
mbe2(i, :) = sum(T_sim2(i, :) - T_test (i, :)) ./ N ;
disp(['训练集数据的MBE为:', num2str(mbe1(i, :))])
disp(['测试集数据的MBE为:', num2str(mbe2(i, :))])
end⛄ 运行结果
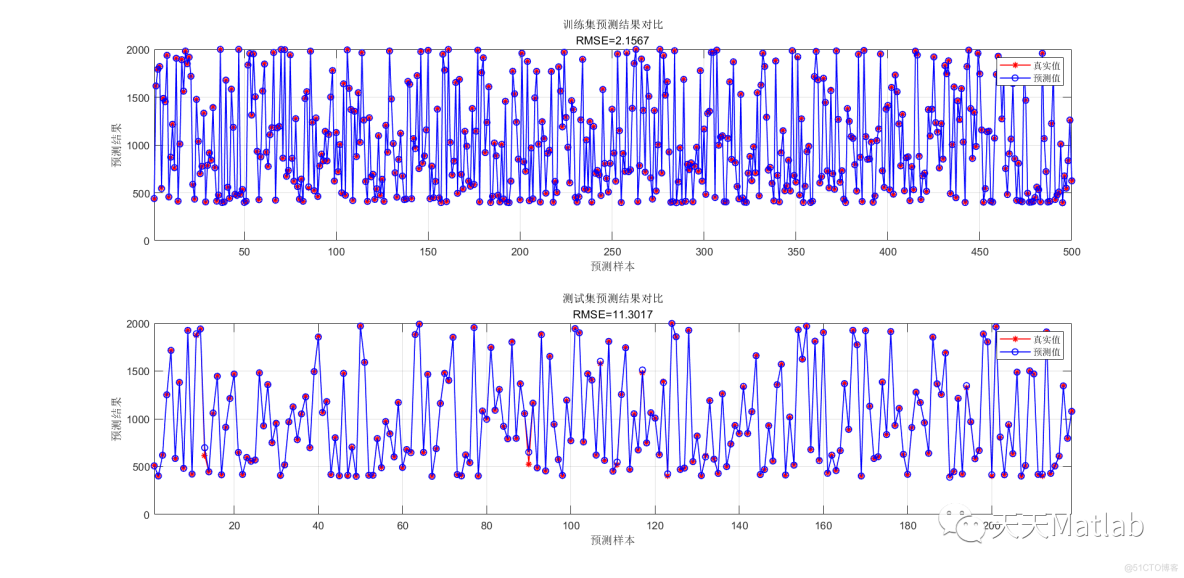
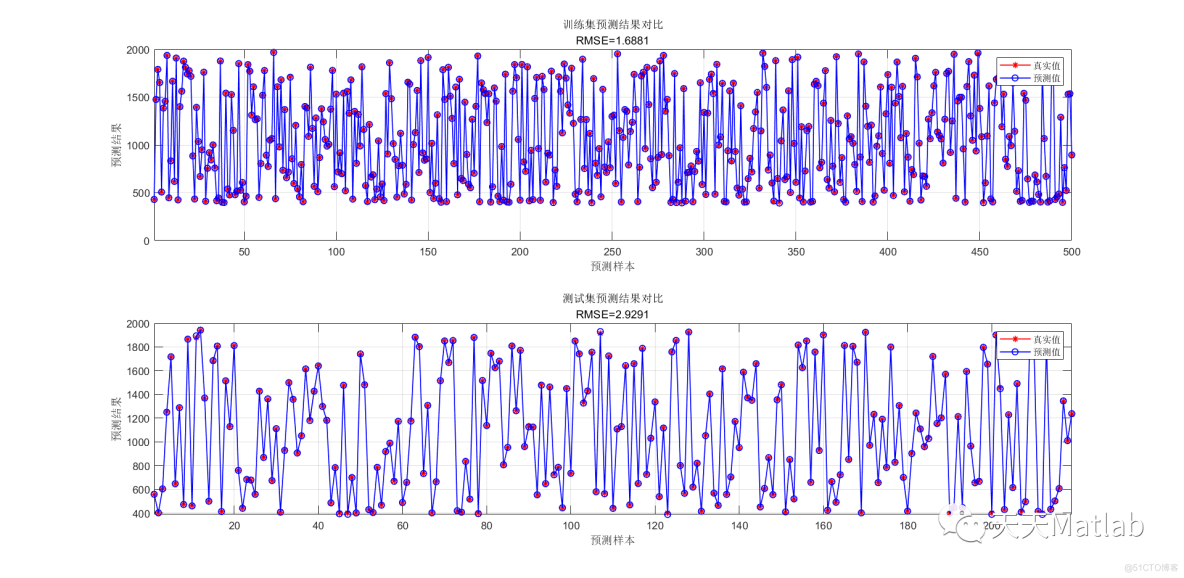
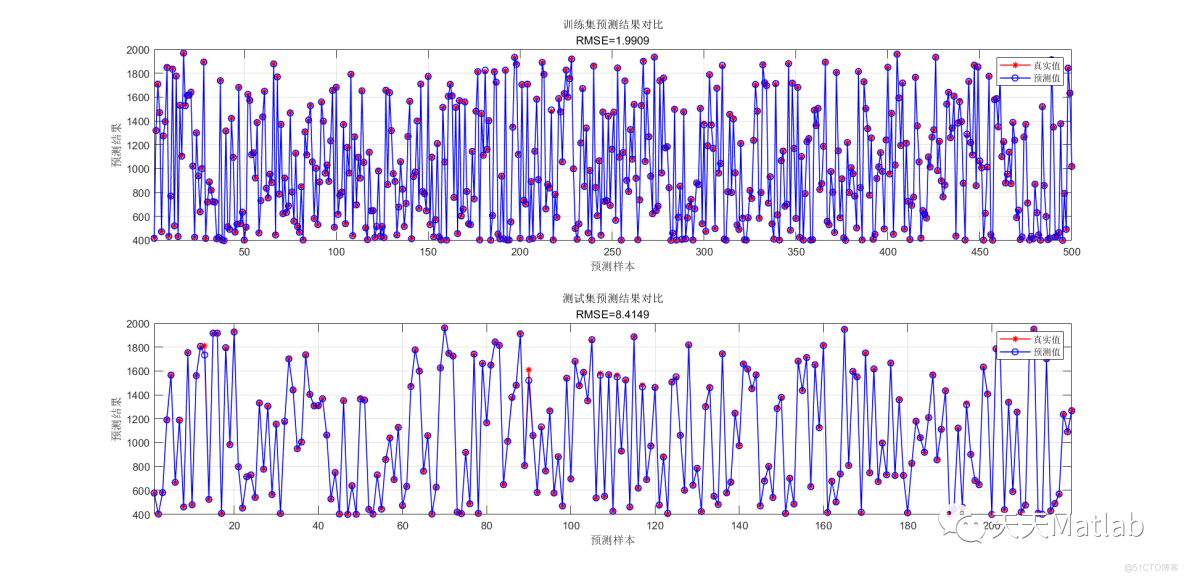




 该文介绍了如何使用Matlab进行基于反向传播(BP)神经网络的回归预测,涉及数据准备、网络结构设计、预处理、训练、验证、测试及结果分析。文中还提供了一段Matlab代码示例,展示了从数据导入到模型训练和性能评估的完整流程。
该文介绍了如何使用Matlab进行基于反向传播(BP)神经网络的回归预测,涉及数据准备、网络结构设计、预处理、训练、验证、测试及结果分析。文中还提供了一段Matlab代码示例,展示了从数据导入到模型训练和性能评估的完整流程。
















 930
930

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








