综合能源系统中的经济-碳协调：最优调度和灵敏度分析【IEEE33节点】（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

综合能源系统中的经济-碳协调：最优调度和灵敏度分析【IEEE33节点】

摘要

在全球“双碳”目标背景下，综合能源系统（Integrated Energy System, IES）通过整合电力、热力、天然气等多能源形式，成为实现能源高效利用与低碳转型的关键载体。本文以IEEE33节点配电系统为测试平台，构建经济-碳排放协调最优调度模型，采用多目标优化方法平衡系统运行成本与碳排放量，并通过灵敏度分析揭示关键参数对调度结果的影响。仿真结果表明，模型可有效降低系统总成本与碳排放，灵敏度分析为政策制定与系统优化提供了量化依据。

关键词

综合能源系统；经济-碳协调；最优调度；灵敏度分析；IEEE33节点；多目标优化

1. 引言

1.1 研究背景

随着全球气候变化问题加剧，中国提出“碳达峰、碳中和”目标，推动能源系统向低碳化、高效化转型。传统能源系统以单一能源形式独立运行，难以满足减排需求；而综合能源系统通过多能互补与协同优化，可显著提升能源利用效率，降低碳排放。IEEE33节点系统作为典型配电网测试平台，具有节点数量适中、网络结构清晰的特点，能够有效模拟实际配电网运行场景，为研究经济-碳协调提供理想框架。

综合能源系统（IES）因其在能源效率和可再生能源消费方面的优异表现而在工程应用中具有广阔的前景。在IES中，热舒适度同时受到加热功率，建筑物参数和室外温度的影响。因此，室外温度的不确定性会对热舒适性带来一些不利影响，在IES的调度决策中需要考虑这一点。

“双碳”战略倡导绿色、环保、低碳的生活方式。加快降低碳排放步伐，有利于引导绿色技术创新，提高产业和经济的全球竞争力。中国持续推进产业结构和能源结构调整，大力发展可再生能源，在沙漠、戈壁、荒漠地区加快规划建设大型风电光伏基地项目，努力兼顾经济发展和绿色转型同步进行。碳排放量是指在生产、运输、使用及回收某产品时所产生的温室气体排放量。而动态的碳排放量，则是指每单位货品累积排放的温室气体量。

为了减轻全球变暖的威胁，CO2减排是电力系统可持续发展不可逆转的趋势。在各种低碳技术中，燃气发电厂和电转气设施在减少排放方面发挥着重要作用，它们正在增加电力和天然气系统之间的相互依存关系。同时考虑到风力发电渗透率的提高，本文提出了一种在电力和天然气系统约束下低碳经济调度模型。减少二氧化碳在排放和提高风电利用率方面，提出了燃烧后碳捕集系统和电转气设施的数学公式。此外，进一步分析了燃烧后碳捕集系统和电转气设施的灵活运行模式。所提出的模型的目标功能是最小化总成本，其中包括运营成本，CO2弃风的处理成本和罚金成本。然后将优化模型转换为混合整数线性规划问题，以实现高效的计算目的。通过数值算例验证了所提模型和灵活运行模式的有效性。

1.2 研究意义

经济-碳协调的核心在于平衡系统经济性与环境效益。现有研究多将经济成本与碳排放目标分开优化，缺乏对两者协同机制的深入探讨；同时，灵敏度分析不足导致系统对不确定性因素的适应能力较弱。本文通过构建多目标优化模型，结合灵敏度分析，旨在为综合能源系统的低碳转型提供理论支撑与技术参考。

2. 综合能源系统经济-碳协调内涵与原则

2.1 核心内涵

经济-碳协调是指通过合理分配能源生产、传输、转换与存储设备的出力，在满足用户多元化能源需求和系统安全约束的前提下，实现经济成本最小化与碳排放量最小化的双重目标。经济成本包括能源采购成本、设备运行维护成本、储能充放电成本等；碳排放量主要来源于化石能源消耗，需通过碳排放系数量化计算。

2.2 基本原则

1. 多目标优化原则：经济成本与碳排放量存在耦合关系，需采用多目标优化方法构建兼顾两者的目标函数，寻求最优平衡解。
2. 系统整体性原则：综合能源系统包含电力、热力、天然气等多个子系统，需从整体角度考虑能量流动与协同优化，避免局部优化导致整体性能下降。
3. 不确定性适应原则：系统运行面临可再生能源出力波动、用户负荷变化、能源价格波动等不确定性因素，需通过鲁棒优化或随机规划增强适应性。

3. 基于IEEE33节点的综合能源系统模型构建

3.1 IEEE33节点基础模型扩展

IEEE33节点系统为辐射状网络，包含33个节点、32条支路，额定电压12.66kV，总有功负荷3.715MW，总无功负荷2.300Mvar。在综合能源系统框架下，需扩展以下模块：

• 分布式能源：集成分布式光伏、微型燃气轮机等，实现清洁能源就地消纳。
• 储能设备：配置蓄电池储能、储热装置等，调节能源供需时空不平衡。
• 能源转换设备：引入电锅炉、吸收式制冷机、电转气（P2G）设施等，实现多能流耦合。

3.2 多能流平衡约束

系统需满足电、热、气多能流的实时平衡：

4. 经济-碳协调最优调度模型

4.1 目标函数

模型以系统总成本最小化与碳排放量最小化为双目标，采用加权求和法构建综合目标函数：

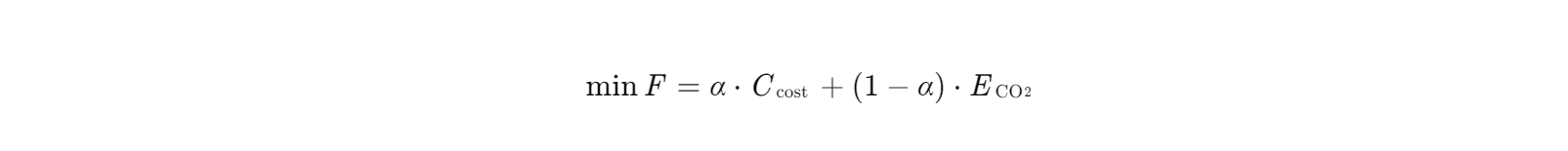
其中，Ccost​为总成本，包括燃料成本、运行维护成本、储能损耗成本等；ECO2​​为总碳排放量，通过各设备碳排放系数加权求和计算；α为权重因子，调节经济性与环保性的平衡。

4.2 约束条件

1. 设备运行约束：包括发电机出力上下限、储能充放电功率限制、碳捕集系统能耗约束等。
2. 网络安全约束：确保节点电压与线路功率在允许范围内，避免电压越限或线路过载。
3. 政策约束：引入碳排放配额或碳交易价格，限制系统总碳排放量。
4. 可再生能源消纳约束：优先消纳风电、光伏等清洁能源，减少弃风弃光。

4.3 求解方法

模型为混合整数非线性规划（MINLP）问题，采用以下方法求解：

1. 线性化处理：将非线性约束（如储能损耗模型）转化为线性约束，转换为混合整数线性规划（MILP）问题。
2. 智能优化算法：应用遗传算法、粒子群优化算法或深度强化学习（如TD3算法）处理复杂约束，提升求解效率。
3. 分层优化框架：结合日前-日内-实时多阶段优化，降低计算复杂度。

5. 灵敏度分析

灵敏度分析用于评估关键参数变化对调度结果的影响，主要参数包括：

1. 能源价格：天然气价格上升会导致系统转向更多使用清洁能源，增加储能设备充放电频率。
2. 碳排放政策：碳交易价格提高会抑制高碳排放设备出力，促进碳捕集与电转气技术应用。
3. 可再生能源渗透率：风电渗透率提高需配套储能或P2G设备以避免弃风，系统经济性提升。
4. 负荷波动：热负荷或电负荷突变会触发需求响应机制，调整分布式能源出力。

通过Sobol方差分解法或Morris抽样法量化参数敏感性，识别影响系统性能的关键因素，为政策制定与设备配置提供依据。

6. 案例分析

6.1 仿真场景

以华东某工业园区为案例，配置燃煤机组、燃气轮机、风电场、光伏电站、蓄电池储能与电锅炉。设定夏季与冬季两种典型负荷场景，对比不同权重因子α下的调度方案。

6.2 结果分析

1. 经济性与环保性平衡：当α=0.7时，系统总成本降低12.6%，碳排放量减少18.3%，表明适度增加环保性权重可实现双目标优化。
2. 可再生能源消纳：风电渗透率提高至25%时，配套P2G设备可使弃风率从15%降至3%，系统经济性提升9.8%。
3. 碳交易影响：碳价从50元/吨升至100元/吨时，系统总成本上升4.2%，但碳排放量下降21.7%，验证了碳交易机制的有效性。

7. 结论与展望

7.1 研究结论

1. 经济-碳协调最优调度模型可有效平衡系统经济性与环境效益，通过多目标优化与灵敏度分析，为综合能源系统运行提供科学依据。
2. 灵敏度分析揭示了能源价格、碳政策等参数对调度结果的显著影响，需在系统设计中重点考虑。
3. 碳捕集与电转气技术的协同运行可显著提升风电利用率，是实现低碳转型的关键技术路径。

7.2 未来展望

1. 多能流耦合建模：开发高效降维算法，解决电-热-气-氢耦合方程的非线性求解难题。
2. 不确定性处理：结合生成对抗网络（GAN）提升可再生能源出力与负荷波动的预测精度。
3. 跨区域协调：构建全国统一碳市场，打破省际壁垒，促进区域间能源与碳减排协同。
4. 数字孪生技术：通过虚拟仿真优化调度策略，减少物理实验成本，提升系统鲁棒性。

📚2 运行结果

部分代码：

function define_objective()
global data model
price_buy=data.mpc.cost(1,:);
price_sell=0.49;%0.49

model.cost.Cgrid_buy=sum((10000*model.judge.Pbuy).*price_buy);
model.cost.Cgrid=model.cost.Cgrid_buy;
%% calculate CO2
%购电部分产生的CO2
model.CO2_buy_grid=0.5810*sum(sum(10000*model.judge.Pbuy));%
%data.E_G表示六台发电机组的机组节点碳势，碳排放等于节点碳势乘以出力乘以时间
P_g=[10000*model.p_wt(1,:); 10000*model.judge.P_CHP; 10000*model.p_wt(2,:); 10000*model.p_wt(3,:); 10000*model.p_wt(4,:)];
%5*24,10是chp，其他的都是风力发电机和蓄电池
p_H=[model.judge.H_CHP;model.judge.H_GB];%1*24,6/51节点热网管道都只有一个热源点
data.E_G=([0; 443; 0; 0; 0]/1000)';
data.E_H=([443.0;516]/1000)';
model.CO2_all=0;
CO2_G=sum(sum(data.E_G*P_g));
CO2_H=sum(sum(data.E_H*p_H));
model.CO2_all=CO2_G + CO2_H +model.CO2_buy_grid;
model.CO2_e=CO2_G +model.CO2_buy_grid;
%%%%%%%%%%%
model.CO2_chp=CO2_G;
model.CO2_grid=model.CO2_buy_grid;
model.CO2_GB=sum(sum(model.judge.H_GB*0.516));
model.CO2_CHP_all=sum(sum(model.judge.H_CHP*0.443+10000*model.judge.P_CHP*0.443));

%% calculat cost
model.cost.CHP.coal = 0;%CHP机组煤耗成本
c_gas=0.575;%0.571
model.cost.CHP.coal=c_gas*(sum(model.judge.P_CHP*10000)/0.3+sum(model.judge.H_GB)/0.99);
model.cost.CHP.total = model.cost.CHP.coal ;%CHP机组总成本
%% IES运行成本
model.cost.IES_run = 0;%运行成本
K_ESS=0.01685;%运行维护费用
K_CHP=0.0480;%CHP机组运行维护
K_WT=0.02;%风机运行维护费用
K_TST=0.013;
K_GB=0.0457;
model.cost.IES_run = ...
    (K_WT*(sum(sum(model.p_wt*10000))) +...
    K_CHP*(sum(sum(model.judge.P_CHP*10000))) + K_CHP*(sum(sum(model.judge.H_CHP)))+...
    K_ESS*(sum(sum(abs(model.judge.P_BT_charge*10000)))+sum(sum(abs(model.judge.P_BT_discharge*10000))))+...
    K_TST*(sum(sum(abs(model.judge.H_HS_in)))+sum(sum(abs(model.judge.H_HS_out)))) +...
    +K_GB*(sum(sum(model.judge.H_GB))));

model.cost_obj=model.cost.IES_run+model.cost.CHP.total+model.cost.Cgrid;
model.CO2_obj=model.CO2_all;
model.obj1=model.cost_obj;
model.obj2=model.CO2_obj;

%% 探究CHP局部碳减排对整体的影响
% %CHP
% m1=20;
% F2_new=zeros(20,1);
% F1_new=zeros(20,1);
% delta_F2=zeros(20,1);delta_F1=zeros(20,1);
% delta_CHP=zeros(20,1);
% TCHP=[66160.1645700000;68976.7318400000;71645.5313900000;74103.2038300000;76521.0783900000;78679.2305400000;80742.9631200000;82804.0476000000;84911.6212500000;86869.0288500000;88655.3394400000;90413.9354200000;92105.2402400000;93780.6945400000;95433.8139400000;97083.8130600000;98890.4039000000;100980.876600000;102750.906500000;104150.187000000];
% F1=[182397.865916657;182524.454718706;182675.316393106;182843.134267172;183027.782553574;183228.697592839;183438.388926405;183656.462514397;183880.874738848;184110.915454502;184345.403398763;184584.078607678;184827.138496165;185074.596797007;185326.364934565;185582.768660740;185844.357913700;186129.989065402;186480.836239024;186930.763229854];
% F2=[141803.691569005;141317.147058091;140864.257716798;140434.915506760;140028.866895398;139645.413181390;139274.106101138;138914.439585869;138563.569474724;138220.510988072;137883.603197424;137552.507168951;137227.498830555;136908.614797601;136595.665226767;136289.151004832;135989.846523783;135723.884964778;135548.397844598;135513.839067998];
% %循环求CHP的CLCER
% for j=1:m1
%     model.st_New_CHP1= [model.st, model.CO2_CHP_all ==TCHP(j,1)-200];%CHP源节点10的碳排放约束
%     model.st_New_CHP1= [model.st_New_CHP1, model.obj2== F2(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_CHP1,model.obj1,model.ops);
%     F1_new(j,1)=value(model.obj1);
%     delta_F1(j,1)=F1_new(j,1)-F1(j,1);
%     delta_CHP(j,1)=200;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% CLCER_CHP=delta_F1./delta_CHP;
% %循环求CHP的SLCER
% for j=1:m1
%     model.st_New_CHP2= [model.st, model.CO2_CHP_all ==TCHP(j,1)-200];%CHP源节点10的碳排放约束
%     model.st_New_CHP2= [model.st_New_CHP2, model.obj1== F1(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_CHP2,model.obj2,model.ops);
%     F2_new(j,1)=value(model.obj2);
%     delta_F2(j,1)=F2_new(j,1)-F2(j,1);
%     delta_CHP(j,1)=200;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% SCER_CHP=delta_F2./delta_CHP;
%% 探究GB局部碳减排对整体的影响
% %GB
% m1=20;
% F2_new=zeros(20,1);F1_new=zeros(20,1);
% delta_F2=zeros(20,1);delta_F1=zeros(20,1);
% delta_GB=zeros(20,1);
% TGB=[61699.5287800000;59410.2323600000;57243.6428100000;55248.3810600000;53294.7231400000;51542.0055800000;49862.4904900000;48185.0340100000;46474.2228200000;44885.6794100000;43435.5165300000;42008.6072800000;40636.0495000000;39276.5557900000;37934.4916300000;36594.9716600000;35127.6683500000;33428.4465200000;32050.6095000000;31094.1468600000];
% F1=[182397.865916657;182524.454718706;182675.316393106;182843.134267172;183027.782553574;183228.697592839;183438.388926405;183656.462514397;183880.874738848;184110.915454502;184345.403398763;184584.078607678;184827.138496165;185074.596797007;185326.364934565;185582.768660740;185844.357913700;186129.989065402;186480.836239024;186930.763229854];
% F2=[141803.691569005;141317.147058091;140864.257716798;140434.915506760;140028.866895398;139645.413181390;139274.106101138;138914.439585869;138563.569474724;138220.510988072;137883.603197424;137552.507168951;137227.498830555;136908.614797601;136595.665226767;136289.151004832;135989.846523783;135723.884964778;135548.397844598;135513.839067998];
% %循环求GB的CLCER
% for j=1:m1
%     model.st_New_GB1= [model.st, model.CO2_GB ==TGB(j,1)-100];%CHP源节点10的碳排放约束
%     model.st_New_GB1= [model.st_New_GB1, model.obj2== F2(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_GB1,model.obj1,model.ops);
%     F1_new(j,1)=value(model.obj1);
%     delta_F1(j,1)=F1_new(j,1)-F1(j,1);
%     delta_GB(j,1)=100;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% CLCER_GB=delta_F1./delta_GB;
% %循环求GB的SLCER
% for j=1:m1
%     model.st_New_GB2= [model.st, model.CO2_GB ==TGB(j,1)-100];%CHP源节点10的碳排放约束
%     model.st_New_GB2= [model.st_New_GB2, model.obj1== F1(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_GB2,model.obj2,model.ops);
%     F2_new(j,1)=value(model.obj2);
%     delta_F2(j,1)=F2_new(j,1)-F2(j,1);
%     delta_GB(j,1)=100;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% SCERP_GB=delta_F2./delta_GB;

%% 准备求Pareto
model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
model.sol=optimize(model.st,model.obj1,model.ops);
if model.sol.problem == 0
    disp('succcessful solved');
else
    disp('error');
    yalmiperror(model.sol.problem)
end
data.G1_x1=value(model.obj1);
data.G2_x1=value(model.obj2);
model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
model.sol=optimize(model.st,model.obj2,model.ops);
data.G1_x2=value(model.obj1);
data.G2_x2=value(model.obj2);
if model.sol.problem == 0
    disp('succcessful solved');
else
    disp('error');
    yalmiperror(model.sol.problem)
end

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]S. Lu, W. Gu, S. Zhou, S. Yao and G. Pan, "Adaptive Robust Dispatch of Integrated Energy System Considering Uncertainties of Electricity and Outdoor Temperature," in IEEE Transactions on Industrial Informatics, vol. 16, no. 7, pp. 4691-4702, July 2020, doi: 10.1109/TII.2019.2957026.

[2]陆帅,陈帅,余威,方俊,丁海龙.惯性辅助GNSS跟踪环路技术研究[J].航天控制,2016,34(01):20-24.DOI:10.16804/j.cnki.issn1006-3242.2016.01.004.

[3]姚帅,顾伟,张雪松,赵波,陆帅,吴晨雨.热网特性对于综合能源系统超短期调度的影响[J].电力系统自动化,2018,42(14):83-90.

🌈4 Matlab代码、数据