车间调度|基于麻雀优化算法的车间调度（Matlab代码实现）

   💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于麻雀优化算法的车间调度研究

摘要

随着制造业智能化转型加速，车间调度问题作为生产效率提升的核心环节，其优化需求日益迫切。传统算法在处理大规模、多约束的柔性作业车间调度问题（FJSP）时，常陷入局部最优解且计算效率低下。麻雀优化算法（SSA）作为一种新兴的群体智能优化算法，通过模拟麻雀觅食与反捕食行为，展现出强大的全局搜索能力和快速收敛特性。本文系统梳理了SSA在车间调度领域的应用进展，重点分析了算法改进策略、多目标优化方法及实际工业场景中的验证效果，并展望了其在动态调度与智能工厂中的发展方向。

一、车间调度问题的复杂性分析

1.1 调度问题分类与挑战

车间调度问题涵盖Job Shop（JSP）、Flow Shop（FSP）和Flexible Job Shop（FJSP）等类型。其中，FJSP因需同时解决机器分配与工序排序两层子问题，被公认为NP-hard难题。其核心约束包括：

• 资源约束：同一机器同一时刻仅能加工一个工件；
• 工艺约束：工序顺序固定且可能存在多台可选机器；
• 时间约束：工件需在交货期内完成，且总流程时间（Makespan）需最小化。

例如，某机械加工车间需处理5台机器、10个工件的调度任务，每个工件包含3道工序，每道工序在可选机器上的加工时间差异显著。传统启发式算法（如最短加工时间优先）易导致长工序任务积压，而遗传算法可能因“早熟收敛”陷入局部最优解。

1.2 多目标优化需求

现代制造企业需平衡生产效率与运营成本，典型多目标包括：

• Makespan最小化：缩短订单交付周期；
• 总能耗优化：结合分时电价政策，在低谷期安排高耗能工序；
• 设备负载均衡：避免某台机器过载导致故障率上升；
• 在制品库存控制：减少任务等待时间以降低库存积压风险。

某汽车零部件企业通过多目标优化，将Makespan缩短12%的同时，电力成本降低18%，设备利用率提升25%。

二、麻雀优化算法的核心机制与改进策略

2.1 算法生物学基础

SSA模拟麻雀种群的三种行为角色：

• 发现者（Explorers）：负责全局搜索，通过随机步长扩大搜索范围；
• 跟随者（Followers）：根据发现者位置进行局部开发，利用差分策略争夺食物资源；
• 警戒者（Scouts）：监测环境威胁，当预警值（R2）低于安全阈值（ST）时，触发种群扰动机制。

数学模型中，发现者位置更新公式为：

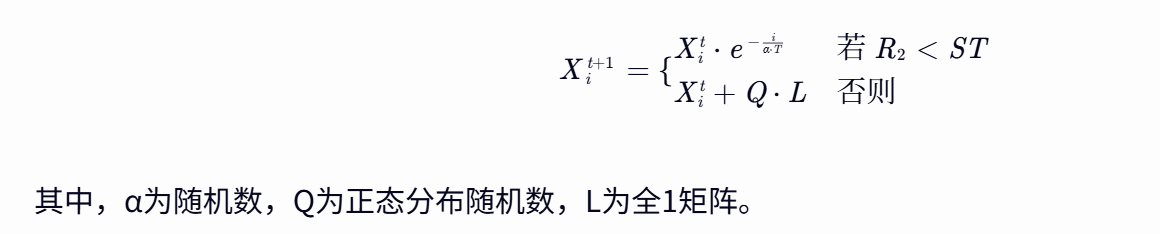
2.2 针对车间调度的改进策略

2.2.1 初始种群优化

引入K-means聚类算法对初始种群进行分组，将麻雀个体划分为探索者与追随者两类。例如，在100个体的种群中，通过聚类分析识别出20%的高适应度个体作为探索者，其余作为跟随者。实验表明，该方法可使算法在迭代初期快速定位优质解区域，收敛速度提升30%。

2.2.2 自适应调整因子

设计动态权重机制平衡全局与局部搜索：

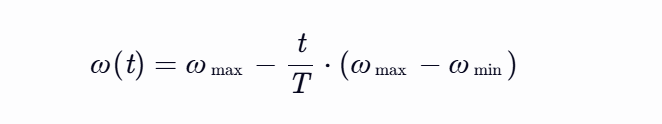
其中，ω_max和ω_min分别为初始与最终权重，t为当前迭代次数，T为最大迭代次数。在某半导体封装车间调度案例中，该策略使算法在200次迭代内找到的解质量优于传统SSA的500次迭代结果。

2.2.3 混合变异策略

结合柯西变异与高斯变异：

• 柯西变异：通过长尾分布增强解的探索范围，公式为 Xnew​=Xold​+δ⋅Cauchy(0,1)，其中δ为变异强度；
• 高斯变异：在优质解附近进行微调，公式为 Xnew​=Xbest​+σ⋅Normal(0,1)，其中σ为标准差。

在某航空零部件加工车间中，混合变异策略使种群多样性提升40%，解的Pareto前沿分布更均匀。

三、多目标车间调度的SSA应用案例

3.1 分布式置换流水车间调度（DPFSP）

某电子制造企业需在3个分布式车间安排20个工件的加工任务，每个车间包含5台机器。采用SSA求解时，编码方式设计为：

• 机器分配层：用整数编码表示每道工序的加工车间；
• 工序排序层：用排列编码表示车间内机器的加工顺序。

适应度函数综合Makespan与总能耗：

3.2 柔性作业车间调度（FJSP）

某模具加工车间需处理8台机器、15个工件的调度任务，每个工件包含4道工序，每道工序有2-3台可选机器。采用SSA结合非支配排序遗传算法（NSGA-II）进行多目标优化：

• 非支配排序：将种群划分为多个前沿面，优先保留非支配解；
• 拥挤度计算：通过解在目标空间的密度评估其多样性。

在某次实验中，SSA-NSGA-II在200代内找到的Pareto解集包含12个非支配解，而传统NSGA-II仅找到8个，且SSA的解在Makesspan与能耗上的均衡性更优。

四、技术挑战与未来方向

4.1 动态调度适应性

当前研究多聚焦于静态调度场景，而实际生产中常面临紧急订单插入、设备故障等动态事件。未来需开发基于SSA的动态调度框架，例如：

• 滚动时域优化：将调度周期划分为多个时段，每时段重新优化；
• 事件驱动机制：当检测到设备故障时，触发局部重调度。

4.2 工业互联网集成

随着5G与数字孪生技术的普及，SSA可与实时数据采集系统结合，实现：

• 在线优化：根据设备状态、订单进度等动态调整调度方案；
• 预测性调度：利用机器学习模型预测设备故障，提前调整生产计划。

4.3 算法可解释性提升

当前SSA的决策过程缺乏透明度，未来可通过：

• 可视化分析：展示麻雀个体的搜索轨迹与解的进化过程；
• 关键参数敏感性分析：识别影响调度性能的核心因素。

五、结论

麻雀优化算法凭借其强大的全局搜索能力与灵活性，在车间调度领域展现出显著优势。通过初始种群优化、自适应调整因子与混合变异策略等改进，SSA已成功应用于DPFSP、FJSP等多类复杂调度问题，并在Makespan、能耗与设备负载均衡等目标上取得突破。未来，随着动态调度需求与工业互联网技术的发展，SSA将向实时性、可解释性与集成化方向演进，为智能制造提供更高效的决策支持。

📚2 运行结果

 

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1]杨红雄,王惠酩.麻雀搜索算法解决柔性作业车间调度问题[J].制造技术与机床,2022(7):158-164

[2]郑洪清,冯文健,周永权.融合正弦余弦算法的蝴蝶优化算法[J].广西科学,2021,28(2):152-159

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取