【迷宫寻路】深度优先搜索和广度优先搜索算法（Matlab实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一文读懂深度优先搜索与广度优先搜索：探索数据迷宫的两大 “神器”

在计算机科学的浩瀚宇宙中，搜索算法是不可或缺的星辰，它们指引着程序在复杂的数据结构中找到目标。其中，深度优先搜索（Depth-First Search，简称 DFS）和广度优先搜索（Breadth-First Search，简称 BFS）堪称最耀眼的双子星。无论是地图导航、游戏 AI，还是网络爬虫，都能看到它们活跃的身影。今天，就让我们一起揭开这两大搜索算法的神秘面纱。

深度优先搜索：一路 “钻到底” 的执着探索者

想象你身处一座巨大的迷宫，深度优先搜索就像是一位勇往直前、不撞南墙不回头的冒险者。它从起点开始，沿着一条路径不断深入探索，直到无法继续前进，才会回溯到上一个节点，选择另一条未探索的路径，继续向下探索，直至找到目标节点或遍历完整个图 / 树结构。

在实现层面，深度优先搜索通常采用递归或者栈来实现。以二叉树为例，使用递归实现时，程序会不断调用自身深入树的节点。而利用栈的话，栈会存储待访问的节点，每次从栈顶取出节点进行访问，并将其子节点压入栈中，以此模拟 “一路深入” 的过程。

深度优先搜索的优点在于，对于某些树状结构或特定的图结构，它能够快速找到一条通往目标节点的路径，并且在空间复杂度上相对较低。然而，它也存在明显的缺陷，如果目标节点离起始节点较远，或者图 / 树结构非常复杂，深度优先搜索可能会在某条路径上深入过远，导致找到的路径并非最优解。例如，在一个迷宫中寻找最短出口路径，深度优先搜索可能会沿着一条曲折的长路径走到尽头，才发现还有更短的路径。

广度优先搜索：“广撒网” 的全面探索者

与深度优先搜索不同，广度优先搜索更像是一位有条不紊、逐层推进的指挥官。它从起始节点开始，先访问与起始节点相邻的所有节点，然后再依次访问这些相邻节点的相邻节点，按照 “层次” 的顺序，一层一层地向外扩展，直到找到目标节点或遍历完整个图 / 树结构。

广度优先搜索通常借助队列来实现。将起始节点放入队列后，每次从队列头部取出一个节点进行访问，并把它所有未访问过的邻居节点添加到队列尾部，以此实现逐层探索的过程。

广度优先搜索最大的优势在于，它总是能找到从起始节点到目标节点的最短路径（在无加权的图结构中）。因为它是按照层次依次探索，不会像深度优先搜索那样在某条路径上过度深入。不过，这种全面的逐层探索方式也带来了较高的空间复杂度，当图 / 树结构规模较大时，需要存储大量的中间节点，可能会占用较多的内存资源。

两大算法的应用场景

在实际应用中，深度优先搜索和广度优先搜索各展所长。深度优先搜索常用于求解迷宫问题、拓扑排序、连通分量查找等场景。比如在游戏开发中，利用深度优先搜索可以生成复杂的迷宫地图；在编译器的语法分析中，拓扑排序也会借助深度优先搜索来实现。而广度优先搜索则在寻找最短路径（如导航软件计算最短行车路线）、最小步数问题（如八数码问题的最优解法）、网络爬虫的网页抓取顺序规划等方面表现出色。

深度优先搜索和广度优先搜索就像计算机科学领域的两种不同解题思路，它们各有千秋，相互补充。理解并掌握这两大搜索算法，不仅能帮助我们在算法竞赛中披荆斩棘，更能为解决实际问题提供强大的工具。未来，随着技术的不断发展，它们或许还会在更多领域发挥重要作用，值得我们持续探索与学习。

📚2 运行结果

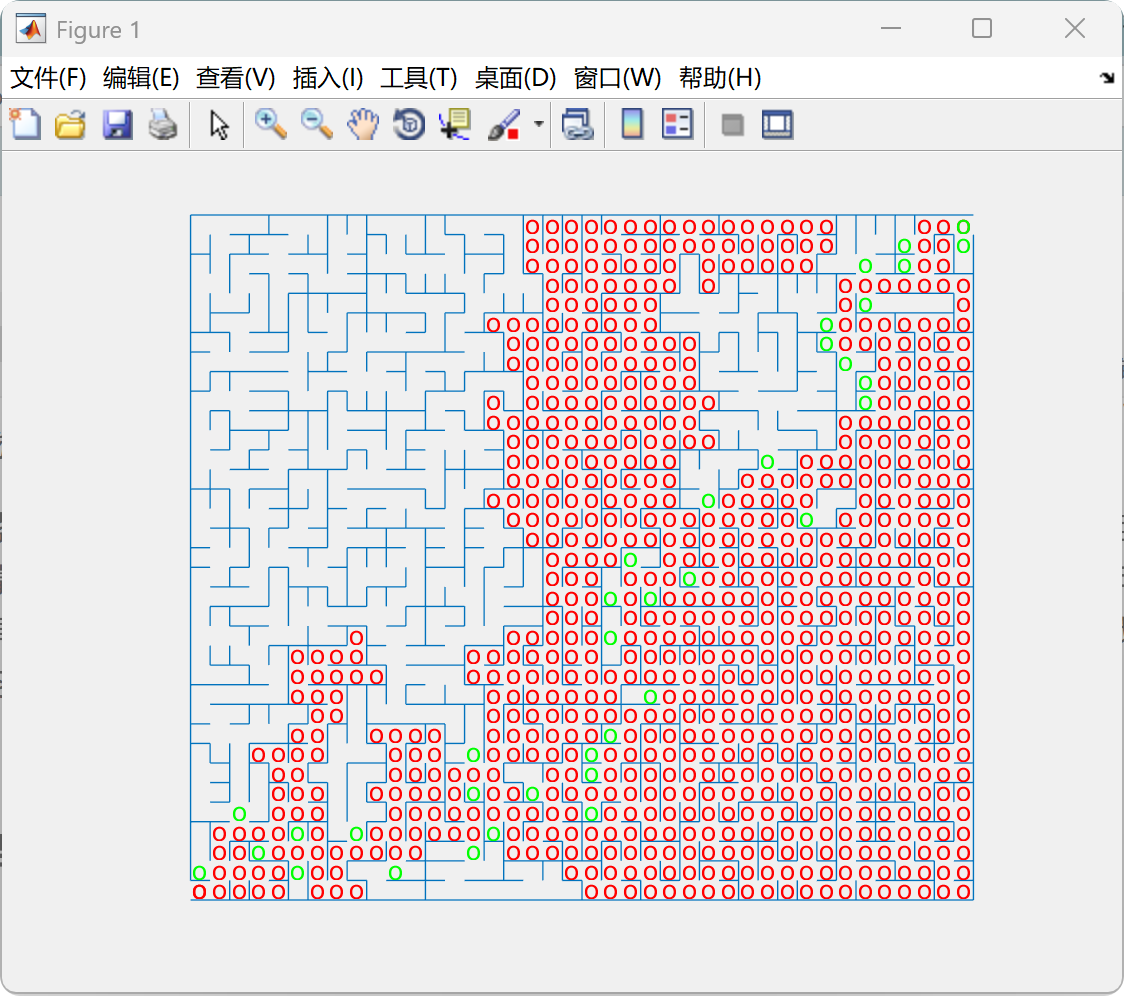
部分代码：

cur_loc = 1;
h = figure();
show_maze(data, h);
draw_cursor(cur_loc, [data.num_rows, data.num_cols], 'r', h);

% TODO: Implement DFS
%{
%Useful java.util.Stack() function calls
%stack=java.util.Stack();
%stack.peek()   %outputs the top object in the stack without removing it
%stack.push(i)  %pushes i onto the stack
%stack.pop()    %outputs the top object in the stack and removes it
%stack.empty()  %checks if the stack is empty
%stack.clear()  %clears stack
%}
stack=java.util.Stack();    %initializing empty stack
N=data.num_rows*data.num_cols;
visited=zeros(N,1); %visited nodes
parent=zeros(N,1);  %parent nodes
stack.push(cur_loc);    %pushing initial position onto stack
%data.goal%location of goals are 35 and 40
goal=1400;
%while (stack.empty()==0) && (cur_loc ~= data.goal(1)) && (cur_loc ~= data.goal(2))
while (stack.empty()==0) && (cur_loc ~= goal)
    i=stack.pop();
    cur_loc=i;
    draw_cursor(cur_loc, [data.num_rows, data.num_cols], 'r', h);
    if (visited(i)==0)   %we have not visited i
        visited(i)=1;   %mark i as visited
        neighbors = sense_maze(i,data); %get neighbors of i
        for j=1:1:size(neighbors,2)   %iterate for all the neighbors to i
            if visited(neighbors(j))==0    %do if not visited
                stack.push(neighbors(j))
                parent(neighbors)=cur_loc;
            end
        end
    end
end
draw_cursor(cur_loc, [data.num_rows, data.num_cols], 'g', h);   %last location in green
fprintf('Number of iterations: %d', nnz(visited));