【路径规划】用于优化 3D 空间中钻孔规划问题的遗传算法（Matlab实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、问题背景与意义

在机械制造、地质勘探、建筑工程等领域，常面临3D 空间中钻孔路径规划的复杂需求，例如航空航天部件的多孔加工、矿山巷道钻孔布局等。该问题的核心是在满足加工工艺、设备约束（如钻头行程、避让障碍物）和精度要求的前提下，优化钻孔顺序、路径长度及空间姿态，以提升效率、降低成本并减少设备损耗。传统启发式算法在处理高维、多约束的 3D 空间问题时易陷入局部最优，而遗传算法（Genetic Algorithm, GA）因其全局搜索能力和鲁棒性，成为解决此类复杂优化问题的有效工具。

二、遗传算法基本框架在钻孔规划中的应用

遗传算法通过模拟生物进化过程（选择、交叉、变异），在解空间中迭代搜索最优解。以下是其在 3D 钻孔规划中的关键设计要素：

（一）染色体编码

直接编码法：将钻孔顺序、空间坐标（x,y,z）及钻头姿态（如倾角、方位角）编码为染色体基因。例如，每个基因对应一个钻孔点，包含坐标向量和姿态参数。

顺序 - 参数分层编码：分离钻孔顺序（如整数排列表示加工顺序）和空间参数（实数编码表示坐标与姿态），便于交叉和变异操作分别优化不同维度。（二）适应度函数设计需综合考虑以下优化目标：

路径最短化：计算相邻钻孔点间的 3D 欧氏距离总和，或考虑钻头进给 / 退刀路径的实际长度

约束满足性：避障约束：确保钻孔路径不与工件内部结构或外部障碍物碰撞。工艺约束：如钻孔深度限制、相邻孔的加工顺序避免应力集中。设备约束：钻头旋转角度范围、进给速度限制。

加工效率：减少空行程时间、换刀次数（若涉及多类型钻头）。适应度函数示例：Fitness=w1⋅L+w2⋅V+w3⋅C1其中，L为总路径长度，V为违反约束的惩罚值，C为工艺成本；w1,w2,w3为权重系数，根据实际需求调整。

（三）遗传操作设计

选择算子
- 轮盘赌选择：基于适应度比例选择个体，适应度越高的染色体被选中的概率越大。
- 精英保留策略：直接保留当前代最优个体至下一代，避免最优解丢失。
交叉算子
- 顺序交叉（OX）：适用于钻孔顺序优化，保留父代部分顺序并交叉插入剩余基因。
- 算术交叉：适用于空间参数（坐标、姿态），通过线性组合生成子代参数（如xchild=α⋅xparent1+(1−α)⋅xparent2）。
变异算子
- 逆转变异：随机反转染色体中某段基因的顺序，扰动钻孔顺序。
- 高斯变异：对空间参数添加高斯噪声（如Δx∼N(0,σ2)），局部搜索更优解。

（四）约束处理

罚函数法：对违反约束的个体在适应度中引入惩罚项（如上述V），迫使算法优先搜索可行解。

可行解空间限定：在交叉和变异后，通过几何运算（如碰撞检测）修正非法解，确保钻孔点位于允许区域内。

三、3D 空间特性带来的挑战与改进策略

（一）高维搜索空间

3D 问题的解空间维度显著高于 2D（如每个钻孔点需 3 个坐标 + 3 个姿态参数），易导致遗传算法收敛速度慢。
改进策略：

引入降维预处理：利用主成分分析（PCA）或空间分割（如八叉树）压缩无效维度。采用混合算法：结合局部搜索算法（如模拟退火、粒子群优化）加速局部寻优，弥补遗传算法局部搜索能力不足。

📚2 运行结果

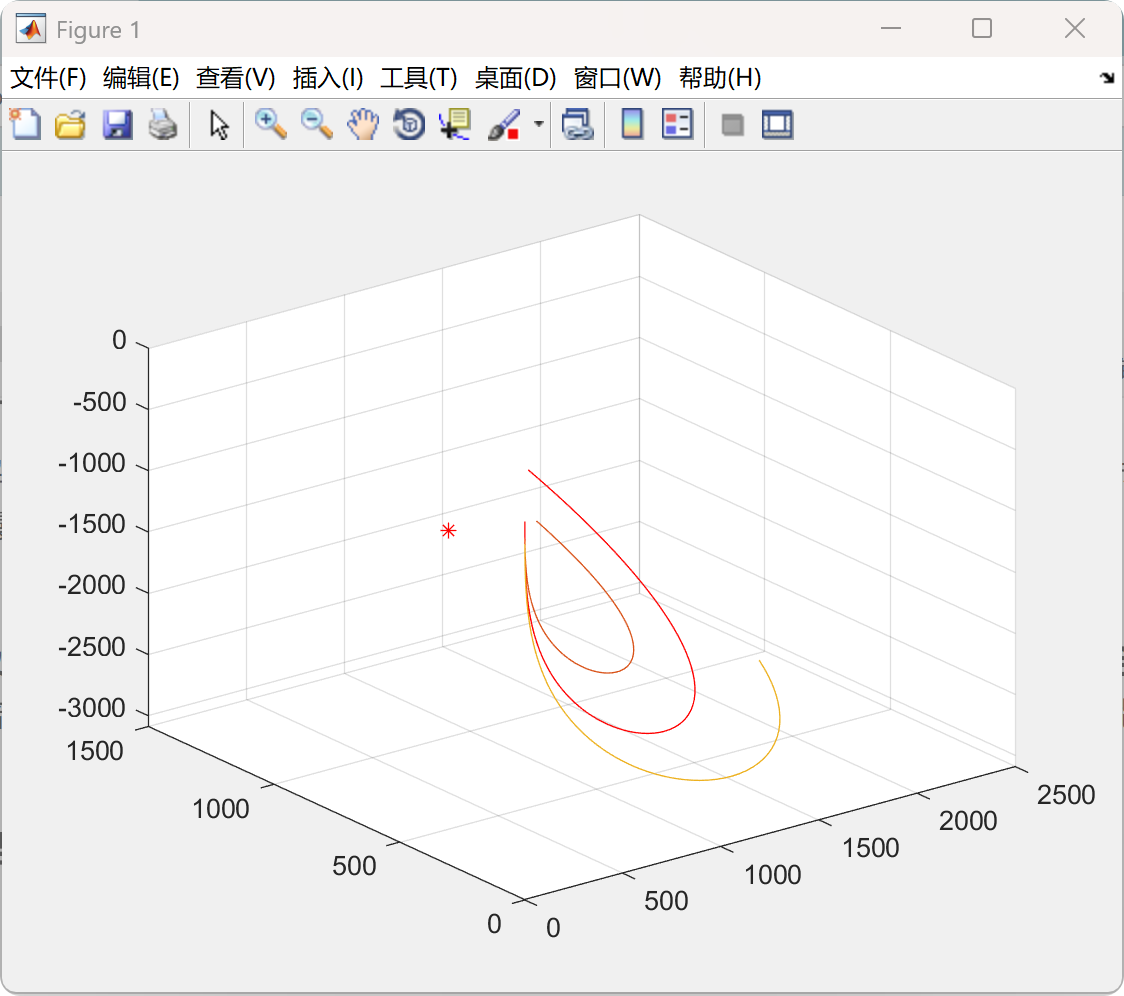
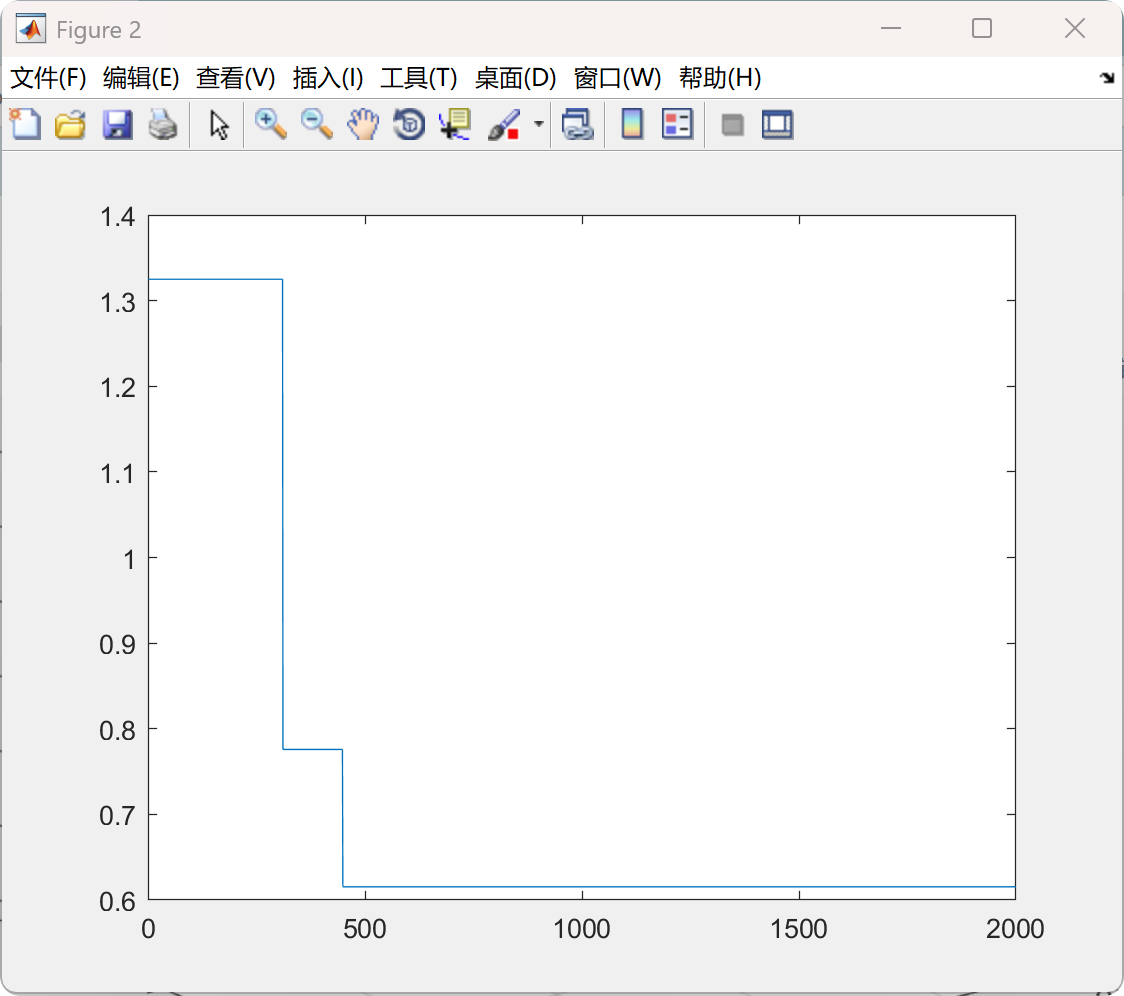
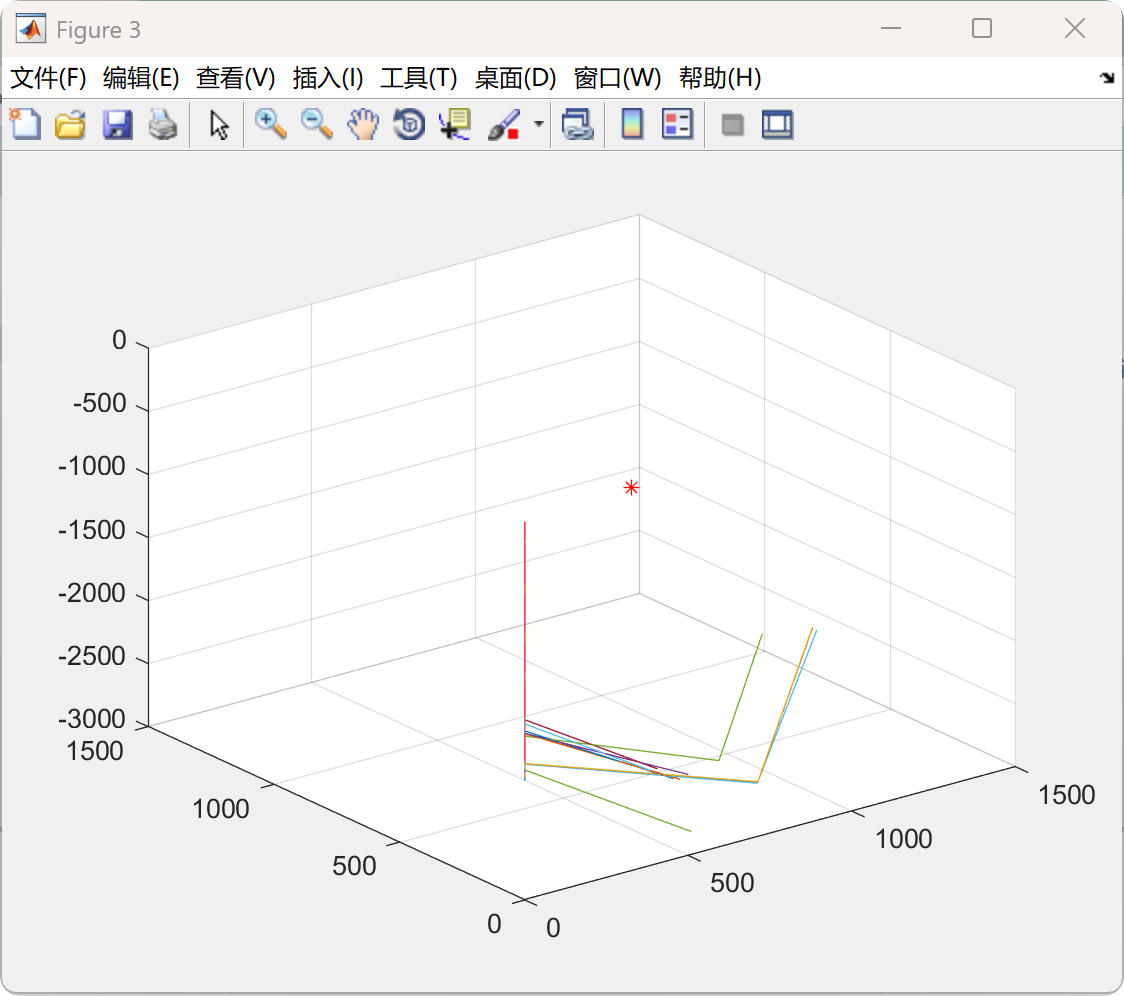
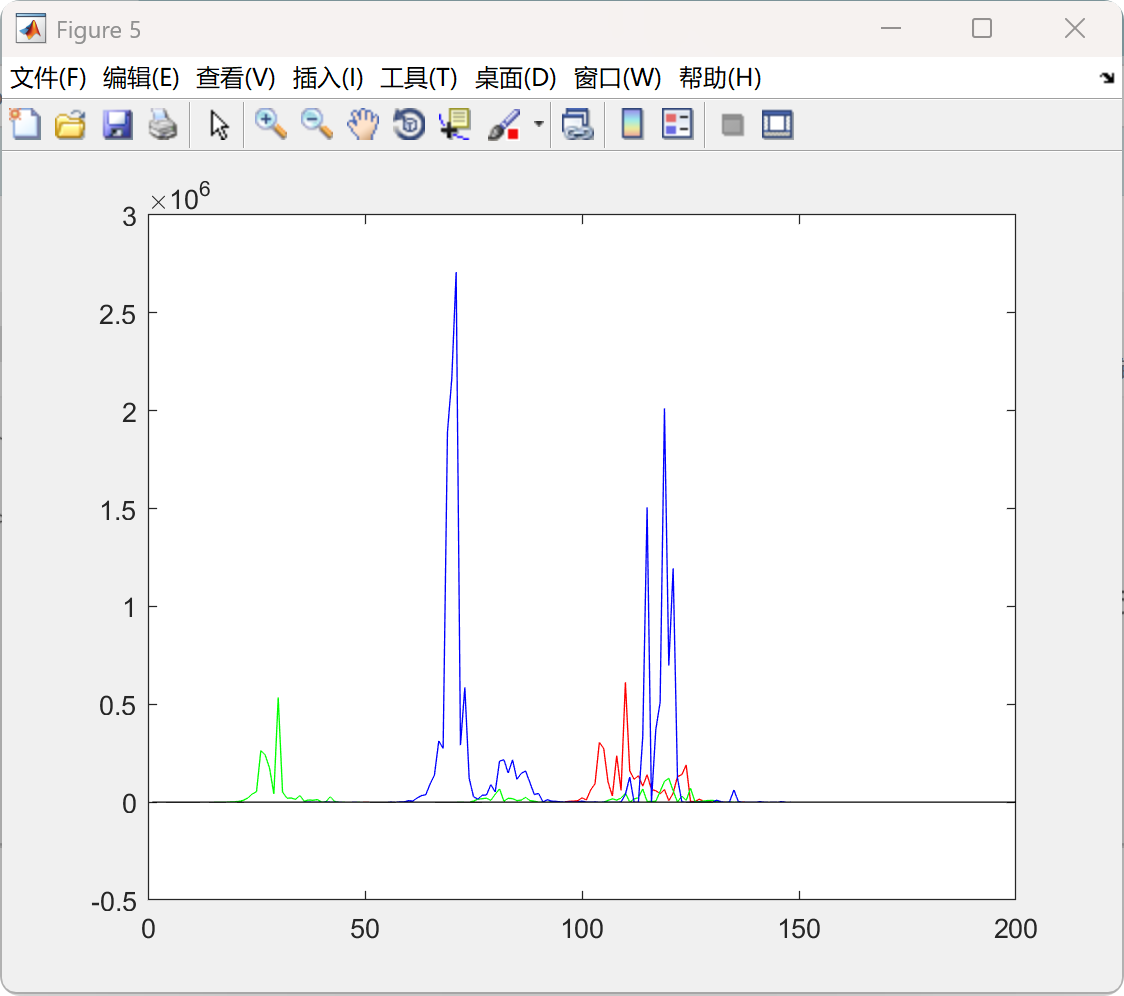
部分代码：

clc
clear all

tic
%parameter initialize
UPPER_LIMIT=100000;
LOWER_LIMIT=-100000;
popSize=200;%population size
offspSize=1400;

n=4;
tau=1/sqrt(2*sqrt(n));
sigma=1;
%initialize population
for i=1:popSize
    population(i)=Trajectory1;
    population(i).sigma_lambda(1)=normrnd(0,sigma);
    population(i).sigma_lambda(2)=normrnd(0,sigma);
    population(i).sigma_lambda(3)=normrnd(0,sigma);
    population(i).sigma_lambda(4)=normrnd(0,sigma);
    
    %random generate initial lambda values
    lambda1=randi([LOWER_LIMIT,UPPER_LIMIT])+rand;
    lambda2=randi([LOWER_LIMIT,UPPER_LIMIT])+rand;
    lambda3=randi([LOWER_LIMIT,UPPER_LIMIT])+rand;
    lambda4=randi([0,UPPER_LIMIT])+rand;
    population(i).lambda(1)=lambda1;
    population(i).lambda(2)=lambda2;
    population(i).lambda(3)=lambda3;
    population(i).lambda(4)=lambda4;
    
    %calculate trajectory by current lambda and C, and fitness
    [population(i).alpha population(i).theta population(i).x population(i).y population(i).z population(i).fitness]=trajGenerate3(lambda1,lambda2,lambda3,lambda4);
    
end

%evolution begins
Gen=1;
figure
best=population(1);
while(Gen<=200)
    
    %print generation and best fitness
    fprintf(['Generation: %i \n',...
        'Best fitness: %f \n',...
        ],Gen,best.fitness);
    fprintf('-------------------- \n');
    
    %generate offsprings
    count=0;
    while(count<offspSize)
        %Parent select and crossover
        p1Index=randi([1,popSize]);
        p2Index=randi([1,popSize]);
        parent1=population(p1Index);
        parent2=population(p2Index);
        offspring1=parent1;
        offspring2=parent2;
        crossover_point1=randi([1,n]);
        crossover_point2=randi([1,n]);
        for i=1:n
            if(i<=crossover_point1)
                offspring1.lambda(i)=parent1.lambda(i);
                offspring2.lambda(i)=parent2.lambda(i);
            else
                offspring1.lambda(i)=parent2.lambda(i);
                offspring2.lambda(i)=parent1.lambda(i);
            end
            if(i<=crossover_point2)
                offspring1.sigma_lambda(i)=parent1.sigma_lambda(i);
                offspring2.sigma_lambda(i)=parent2.sigma_lambda(i);
            else
                offspring1.sigma_lambda(i)=parent2.sigma_lambda(i);
                offspring2.sigma_lambda(i)=parent1.sigma_lambda(i);
            end
        end
        
        
        %mutate offsprings sigma first, then lambda values
        for i=1:n
            offspring1.sigma_lambda(i)=offspring1.sigma_lambda(i)*exp(tau*normrnd(0,sigma));
            offspring1.lambda(i)=offspring1.lambda(i)+offspring1.sigma_lambda(i)*normrnd(0,sigma);
            
            offspring2.sigma_lambda(i)=offspring2.sigma_lambda(i)*exp(tau*normrnd(0,sigma));
            offspring2.lambda(i)=offspring2.lambda(i)+offspring2.sigma_lambda(i)*normrnd(0,sigma);
        end
        
        %evaluate offspring fitness and trajectory
        [offspring1.alpha offspring1.theta offspring1.x offspring1.y offspring1.z offspring1.fitness]=trajGenerate3(offspring1.lambda(1),offspring1.lambda(2),offspring1.lambda(3),offspring1.lambda(4));
        [offspring2.alpha offspring2.theta offspring2.x offspring2.y offspring2.z offspring2.fitness]=trajGenerate3(offspring2.lambda(1),offspring2.lambda(2),offspring2.lambda(3),offspring2.lambda(4));
        
        offsprings(count+1)=offspring1;
        offsprings(count+2)=offspring2;
        count=count+2;
    end
    
    %survival selection (u+lambda) with replacement
%     newpopulation=[population offsprings];
%     [~,index]=sort([newpopulation.fitness]);
%     temp=newpopulation(index);
%     population=temp(1:popSize);
[~,index]=sort([offsprings.fitness]);
temp=offsprings(index);
    if(temp(1).fitness<best.fitness)
        best=temp(1);
    end
    population=temp(1:popSize);
    
    %store values
    bestFitness(Gen)=population(1).fitness;
    sigmas(Gen,:)=population(1).sigma_lambda;


    %next generation and plot
    Gen=Gen+1;
    if(mod(Gen,10)==0)
        plot3(population(1).x,population(1).y,population(1).z)
        hold on
    end
    
    
end
toc
plot3(population(1).x,population(1).y,population(1).z,'r')
hold on
plot3(1400,1400,-2000,'r*');
grid on

figure
plot(bestFitness)

figure
plot(sigmas(:,1),'r')
hold on
plot(sigmas(:,2),'g')
hold on
plot(sigmas(:,3),'b')