【选址问题】卡尔曼滤波器和粒子滤波器的代码，用于解决船只位置的问题（Matlab实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/147537572

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

卡尔曼滤波器

原理基础

卡尔曼滤波器是一种针对线性系统且噪声服从高斯分布情况的最优递归滤波器。它借助系统的动态模型与测量模型，在预测与更新这两个步骤中不断迭代，从而对船只的状态（位置、速度等）进行最优估计。预测步骤依据系统的动态特性对下一时刻的状态进行预估，更新步骤则结合实际测量值对预测结果进行修正。

代码实现关键要点

参数初始化：需要设定初始状态估计值、状态协方差矩阵、状态转移矩阵、测量矩阵、过程噪声协方差矩阵和测量噪声协方差矩阵。
预测步骤：依据状态转移矩阵对状态进行预测，同时更新协方差矩阵以反映预测的不确定性。
更新步骤：通过计算卡尔曼增益，结合测量值对预测状态进行校正，进而得到更精准的状态估计。

粒子滤波器

原理基础

粒子滤波器是一种基于蒙特卡罗模拟的滤波方法，适用于非线性、非高斯系统。它借助一组随机样本（粒子）来近似表示系统状态的概率分布。在每个时间步，粒子根据系统的动态模型进行状态转移，并依据测量值对粒子的权重进行更新，最后通过重采样去除权重小的粒子，保留并复制权重大的粒子。

代码实现关键要点

粒子初始化：随机生成一组粒子，每个粒子代表一个可能的状态，并为其分配初始权重。
预测步骤：依据系统的动态模型对每个粒子的状态进行更新。
更新步骤：根据测量值计算每个粒子的权重，权重反映该粒子与测量值的匹配程度。
重采样步骤：根据粒子的权重对粒子进行重采样，以防止粒子退化。

总结

卡尔曼滤波器适用于线性高斯系统，计算效率高；粒子滤波器适用于非线性非高斯系统，能处理更复杂的情况。上述代码提供了基本的实现框架，你可以根据实际需求调整参数和模型，以更好地解决船只位置估计问题。

📚2 运行结果

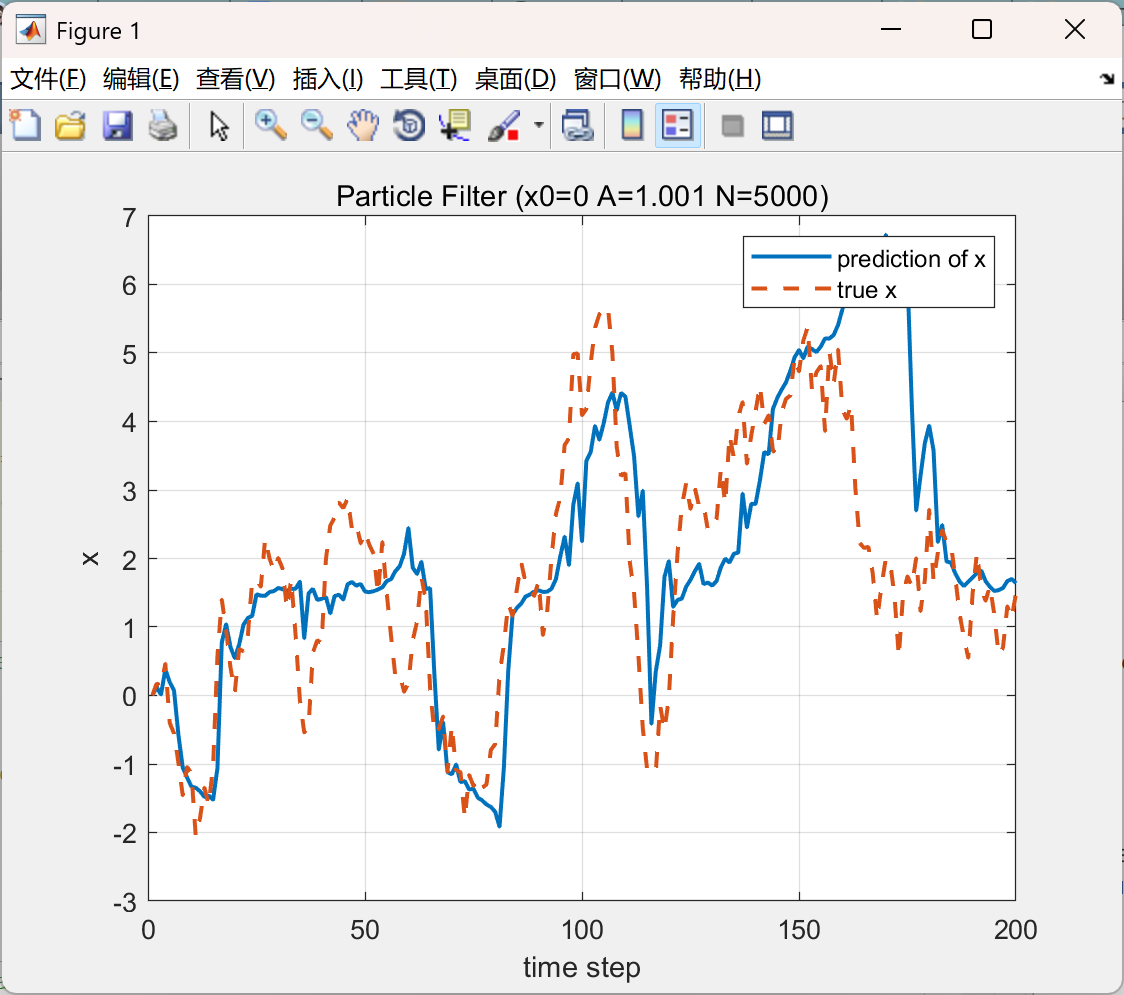
部分代码：

clear all;
% x(t+1) = Ax(t) + w
% y(t) = d(x(t)) + v
% w ~ N(0, Q)
% v ~ N(0, R)

%% Parameters
A = 1.001; % transition matrix
Q = 0.25; % covariance of noise w
R = 0.3; % covariance of noise v
x0 = 0; % initial state
len = 200; % length of the sequence
N = 5000; % number of particle

%% Initialization
x_true = zeros(1, len);
x_pred = zeros(1, len);
y = zeros(1, len);
x_true(1) = x0;
x_pred(1) = x0;
seed = 7;

%% Preparation of true location
randn('state', seed);
y(1) = d(x_true(1)) + normrnd(0, R^0.5);

for i = 2:len
    x_true(i) = A * x_true(i - 1) + normrnd(0, Q^0.5);
    y(i) = d(x_true(i)) + normrnd(0, R^0.5);
end

%% Prediction
particle = zeros(1, N) + x0; % initialize particles with x0
w = zeros(1, N) + 1 / N; % initialize weights with 1/N

for i = 2:len
    disp(i)
    % p(x(t)|x(t-1))
    particle = A .* particle + normrnd(0, Q^0.5, [1, N]);
    % w = p(y|x)*(1/N)
    w = exp(- (y(i) - d(particle)).^2 / (2 * R)) / sqrt(2 * pi * R);
    % normalization using 1/N
    w = w ./ sum(w);
    % resampling and update particle
    for n = 1:N
        particle(n) = particle(find(rand <= cumsum(w), 1));
    end

    % estimated variable
    x_pred(i) = mean(particle);
end

%% Evaluation
mse = sum((x_pred - x_true).^2) ./ size(x_true, 2);
disp(['MSE:', num2str(mse)]);

%% Illustration
plot(x_pred, '-', 'linewidth', 1.5)
hold on
plot(x_true, '--', 'linewidth', 1.5)
xlabel('time step');
ylabel('x');
legend('prediction of x', 'true x');
grid on;
title(['Particle Filter (x0=', num2str(x0), ' A=', num2str(A),' N=', num2str(N), ')']);
saveas(gcf, 'Particle.png');