【信号处理】MUSIC多信号分类算法（Matlab实现）

荧光Matlab

已于 2024-12-25 19:51:06 修改

阅读量988

点赞数 8

CC 4.0 BY-SA版权

文章标签：信号处理

于 2024-12-25 19:44:45 首次发布

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/144726615

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、算法背景与基本原理

多信号分类算法是一种在阵列信号处理领域应用广泛且非常重要的高分辨率空间谱估计算法。它诞生的背景源于传统的基于波束形成等空间谱估计方法在分辨多个相近信号源时存在分辨率不足的问题，难以准确区分角度间隔较小的多个目标信号。其基本原理是基于对阵列接收数据的协方差矩阵进行特征分解。假设存在一个由多个传感器组成的阵列（例如均匀线阵、面阵等）接收来自不同方向的多个信号源发射的信号，同时夹杂着噪声。该算法首先构建接收信号的协方差矩阵，然后对其进行特征分解，将其分解为对应信号子空间和噪声子空间的特征向量。理论上，信号子空间由与信号相关的特征向量张成，而噪声子空间则由与噪声相关的特征向量构成，并且信号子空间和噪声子空间是相互正交的。基于这一正交特性，通过计算某一导向矢量（与信号入射方向相关的矢量）与噪声子空间的正交性度量，来判断对应方向是否存在信号源，当正交性度量达到特定条件（比如最小值等情况）时，就可以确定信号源的方位等信息。

二、算法的特点与优势

高分辨率特性：MUSIC算法最突出的优势之一就是相较于传统方法，它具有较高的空间分辨率。即使多个信号源的入射角度间隔很小，也能够较为准确地将它们分辨出来，从而精确地确定各个信号源所处的方位，这对于在复杂环境下对多个目标进行定位等应用场景来说十分关键。不需要信号先验知识：它在一定程度上不需要对信号的具体波形、幅度等详细的先验知识有过多依赖，仅通过对阵列接收数据的处理和空间特性的挖掘就能实现信号源方位估计，相对来说应用起来更为灵活，可适用于多种不同类型的信号情况。

三、算法的计算步骤

1. 数据采集与协方差矩阵构建：利用阵列中的各个传感器接收信号，在一定时间内采集足够的数据样本，然后根据这些样本构建接收信号的协方差矩阵。这一步骤中，要确保数据采集的准确性以及对噪声等干扰因素的合理考虑，协方差矩阵的准确构建是后续准确分析的基础。 2. 特征分解：对所构建的协方差矩阵进行特征分解操作，通过合适的数学算法（如特征值分解算法等），将其分解为信号子空间对应的特征向量和噪声子空间对应的特征向量，这一步涉及到较为复杂的矩阵运算，但现代计算工具能够较好地辅助完成。 3. 谱峰搜索：基于信号子空间和噪声子空间的正交关系，针对一系列可能的信号入射方向，计算对应的导向矢量与噪声子空间的正交性度量（通常以某种形式的函数表示，如MUSIC谱函数），然后通过搜索该函数的峰值来确定信号源的方位。这一搜索过程需要在一定的角度范围内进行遍历，以找到所有满足条件的信号源方向对应的峰值。

四、应用领域

雷达领域：在雷达探测系统中，尤其是面对多个空中目标且目标方位较为接近的情况时，MUSIC算法能够帮助准确分辨不同目标的角度位置，提升雷达对多目标的监测和跟踪能力，保障空中交通管制、防空预警等任务的有效开展。通信领域：例如在多用户通信场景下，基站接收来自多个移动终端的信号，运用MUSIC算法可以区分不同用户信号的来向，便于实现空间复用、干扰抑制等功能，提高通信系统的容量和通信质量。声纳系统：在水下利用声纳进行目标探测时，若存在多个水下目标同时发出声音或者反射回波，MUSIC算法可以凭借其高分辨率特性准确判断各个目标的方位，无论是军事上的反潜、水下目标搜索还是民用的海洋资源勘探、渔业探测等方面都有着重要应用价值。

五、局限性及改进方向

局限性：MUSIC算法的计算复杂度相对较高，尤其是在大规模阵列以及需要高分辨率角度搜索时，计算量会显著增大，对硬件计算资源要求较高；而且其性能在一定程度上依赖于对阵列结构的假设以及信号与噪声的特性假设，当实际情况与假设偏离较大时，可能会出现分辨率下降、估计误差增大等问题。改进方向：一方面，研究人员致力于通过优化算法结构、采用快速计算算法（如基于快速傅里叶变换等的快速MUSIC算法变体）来降低计算复杂度，提高运算效率；另一方面，结合自适应滤波、机器学习等其他技术手段，不断放宽对假设条件的严格要求，增强算法在复杂实际环境中的鲁棒性和适应性，使其能够更好地服务于多信号分类的实际应用需求。

📚2 运行结果

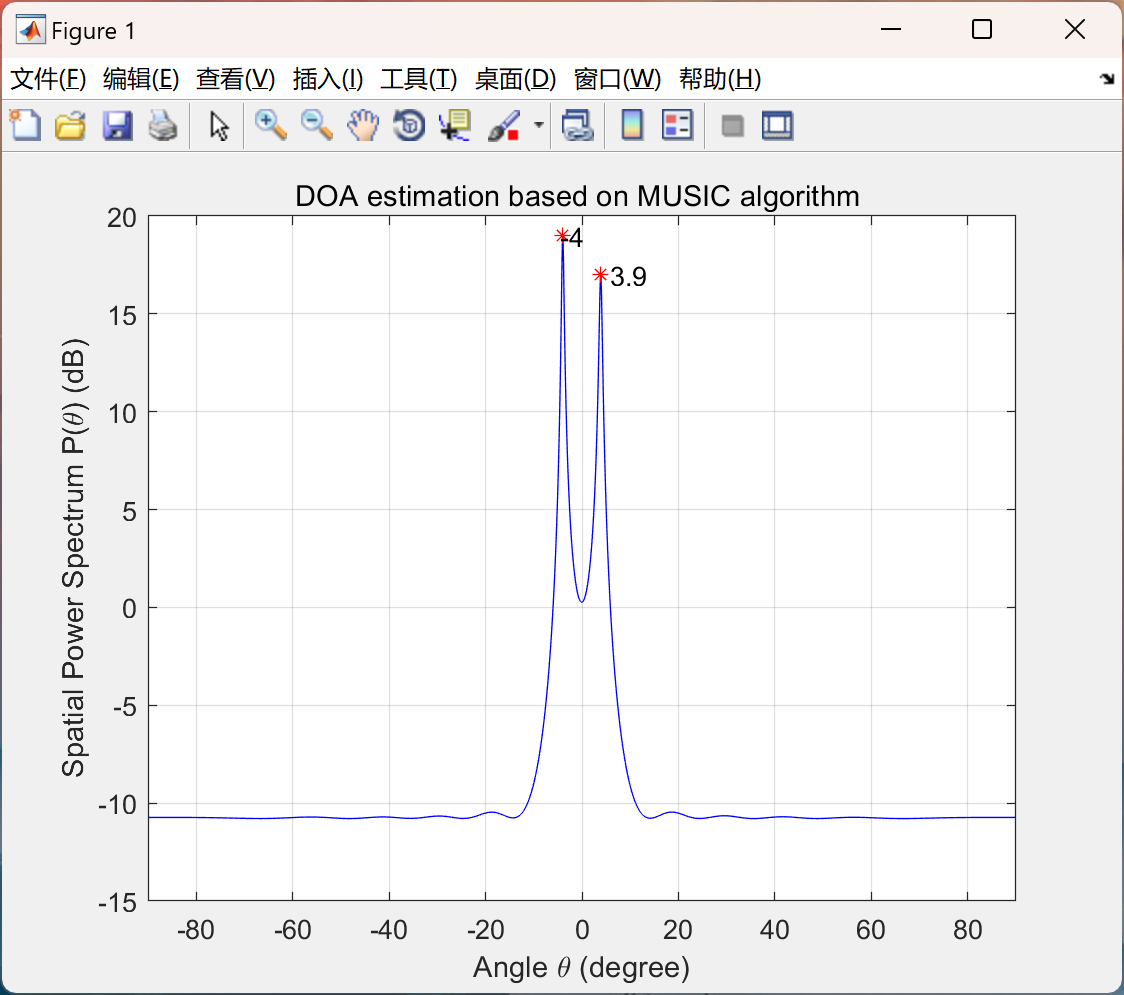
主函数部分代码：

clc 
clear
close all
format compact     

DOA = [-4 4];      %Direction of arrival (Degree)
T   = 500;         %Snapshots (or Samples)
K   = length(DOA); %The number of signal source(or traget) 
Nr  = 12;          %Number of receiver's antennas 
lambda = 150;      %Wavelength 
d   = lambda/2;    %Receiver's antennas spacing
SNR = 1;           %Signal to Noise Ratio (dB)
A = zeros(Nr,K);   %Steering Matrix 
for k=1:K 
    A(:,k) = exp(-1j*2*pi*d*sind(DOA(k))*(0:Nr-1)'/lambda); %Assignment matrix 
end 
Vj = diag(sqrt((10.^(SNR/10))/2));
s = Vj* ( randn(K,T) + 1j*randn(K,T) );
noise = sqrt(1/2)*(randn(Nr,T)+1j*randn(Nr,T));

X = A*s; 
X = X+noise;      %Insert Additive White Gaussain Noise (AWGN) 

%% MUSIC (MUltiple SIgnal Classification)
Rx = cov(X');                     %Data covarivance matrix 
[eigenVec,eigenVal] = eig(Rx);    %Find the eigenvalues and eigenvectors of Rx 
Vn = eigenVec(:,1:Nr-K);          %Estimate noise subspace (Note that eigenvalues sorted ascendig on columns of "eigenVal")
theta = -90:0.05:90;       %Grid points of Peak Search 
for i=1:length(theta) 
    SS = zeros(Nr,1); 
    SS = exp(-1j*2*pi*d*(0:Nr-1)'*sind(theta(i))/lambda);
    PP = SS'*(Vn*Vn')*SS;
    Pmusic(i) = 1/ PP; 
end
Pmusic = real(10*log10(Pmusic)); %Spatial Spectrum function
[pks,locs] = findpeaks(Pmusic,theta,'SortStr','descend','Annotate','extents');
MUSIC_Estim = sort(locs(1:K))

figure;
plot(theta,Pmusic,'-b',locs(1:K),pks(1:K),'r*'); hold on
text(locs(1:K)+2*sign(locs(1:K)),pks(1:K),num2str(locs(1:K)'))

xlabel('Angle \theta (degree)'); ylabel('Spatial Power Spectrum P(\theta) (dB)') 
title('DOA estimation based on MUSIC algorithm ') 
xlim([min(theta) max(theta)])