【路径规划】用于 MATLAB 的杜宾斯快速扩展随机树（Matlab实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/144544425

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

基本概念

快速扩展随机树（RRT）是一种在路径规划领域应用广泛的算法。它基于随机采样的思想，通过不断在空间中扩展树结构来探索环境，逐步构建出从起始点到目标点的可行路径。而杜宾斯快速扩展随机树（Dubins-RRT）则是在常规RRT的基础上，融入了杜宾斯曲线（Dubins Curves）相关理论。杜宾斯曲线是用于描述在特定约束（比如车辆等具有最小转弯半径限制的运动体）下，从一个初始状态到另一个状态的最短路径曲线形式，通常应用于移动机器人、自动驾驶车辆等领域的路径规划中。

在MATLAB中的实现意义 MATLAB作为一款功能强大的科学计算和编程软件，有着丰富的数学函数库、可视化工具以及易于上手的编程环境。将Dubins-RRT算法在MATLAB中实现，可以充分利用这些优势。比如利用其矩阵运算能力高效地处理坐标、状态等数据的计算；借助可视化功能直观地展示随机树的扩展过程、生成的路径以及环境中的障碍物等情况，方便开发者调试算法、分析路径规划效果。并且对于科研人员来说，能便捷地基于MATLAB平台进行相关算法改进、性能对比等研究工作，对于实际工程应用中涉及到路径规划的项目，也可以通过MATLAB快速进行方案验证和原型开发。

主要功能与应用场景

功能方面：环境建模与探索：能够依据设定的地图范围、障碍物信息等构建相应的环境模型，在这个环境中不断通过随机采样点扩展树结构，逐渐探索出可达的空间区域，找到可能通向目标的分支。

路径生成：结合杜宾斯曲线的特点，为具有运动学约束的物体规划出符合其转弯半径等限制条件的、相对优化的路径，确保生成的路径在实际中是可执行的。路径优化与调整：可以根据一定的优化准则，比如路径长度最短、经过的危险区域最少等，对初步生成的路径进行进一步优化，同时也能在遇到动态障碍物等情况时，实时调整已规划好的路径。

应用场景：机器人领域：无论是室内服务机器人在房间内导航，还是工业机器人在车间复杂环境中移动执行任务，Dubins-RRT都可以为其规划出合理的运动路径，避免碰撞障碍物，提高工作效率。自动驾驶车辆：考虑到车辆本身不能随意转弯，存在最小转弯半径的限制，该算法可帮助自动驾驶汽车在城市道路、停车场等场景下规划行驶路径，实现安全、高效地从起点驶向目的地。无人机飞行路径规划：针对无人机有限的机动性能，规划出符合其飞行特性的轨迹，使其能顺利绕过禁飞区等障碍区域，完成诸如航拍、物资运输等任务。

算法的优势与局限性

优势：对复杂环境适应性较好：由于采用随机采样扩展树的方式，对于形状不规则、存在大量障碍物的复杂环境，有较大概率能探索到可行的路径，不需要对整个环境进行精确的、事先的数学建模。计算效率相对可观：相较于一些穷举式的路径规划算法，它通过有针对性地随机采样和逐步扩展，在很多情况下能较快地找到一条可用路径，尤其是在高维空间中也能展现出一定的效率优势。考虑运动学约束：结合杜宾斯曲线融入运动学约束条件，使规划出的路径贴合实际物体的运动能力，避免规划出不符合实际执行情况的路径。

局限性：路径最优性不能完全保证：虽然可以进行一定程度的优化，但基于随机采样的本质，不能确保每次得到的路径都是全局最优的，可能存在更短或者性能更好的路径未被探索到。依赖参数设置：像采样范围、扩展步长、树的生长概率等参数对算法的性能和最终路径结果影响较大，不合适的参数设置可能导致算法收敛过慢甚至找不到可行路径，需要一定的经验和反复试验来确定合适参数。在动态环境实时性挑战：面对动态变化频繁的环境，比如快速移动的障碍物等情况，算法的实时更新和重新规划路径的能力存在一定局限，可能无法及时响应环境变化而导致路径失效。总之，用于MATLAB的杜宾斯快速扩展随机树是一种在路径规划领域很有价值的工具，虽然存在一些局限性，但在很多实际应用场景中都能发挥重要作用，并且随着相关研究的不断深入，其性能也有望进一步提升。

📚2 运行结果

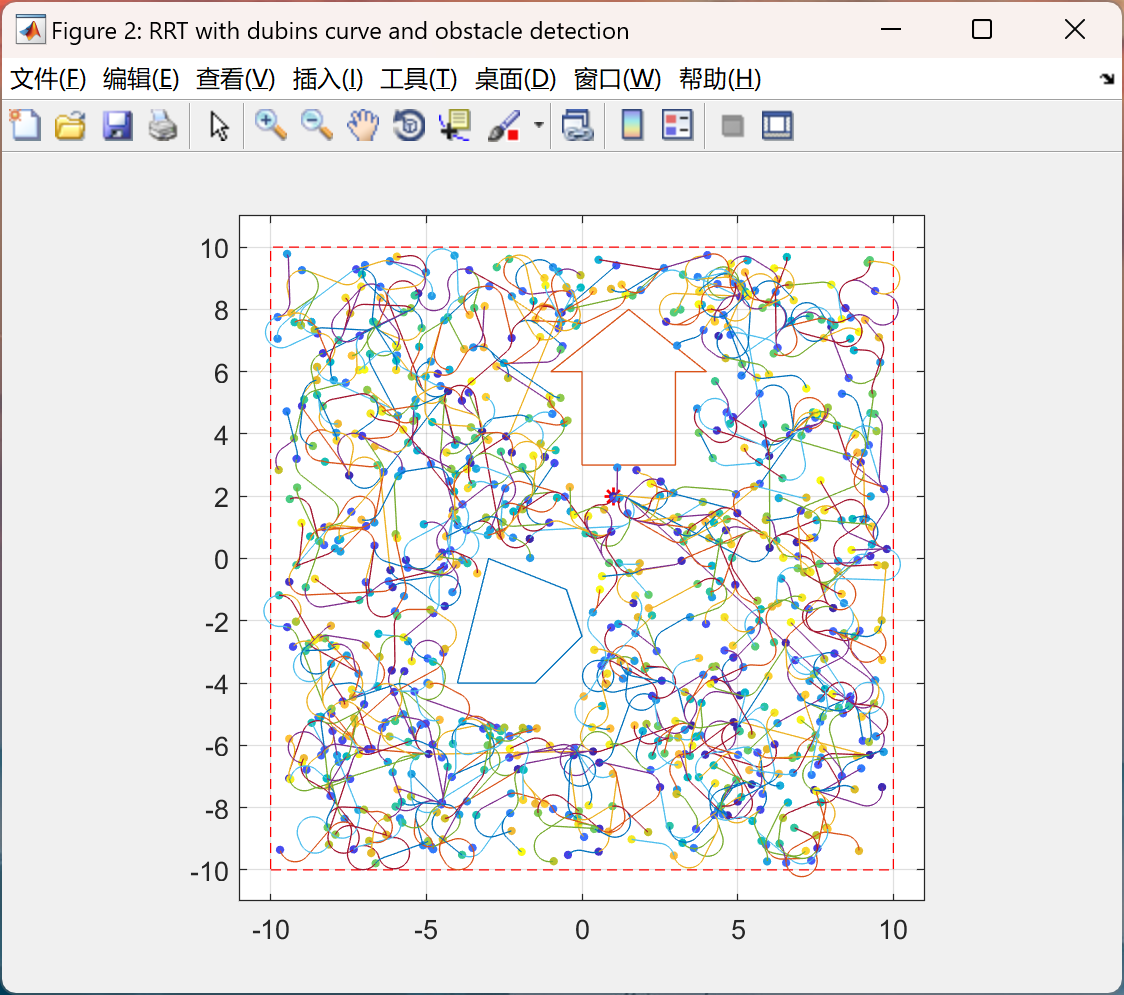
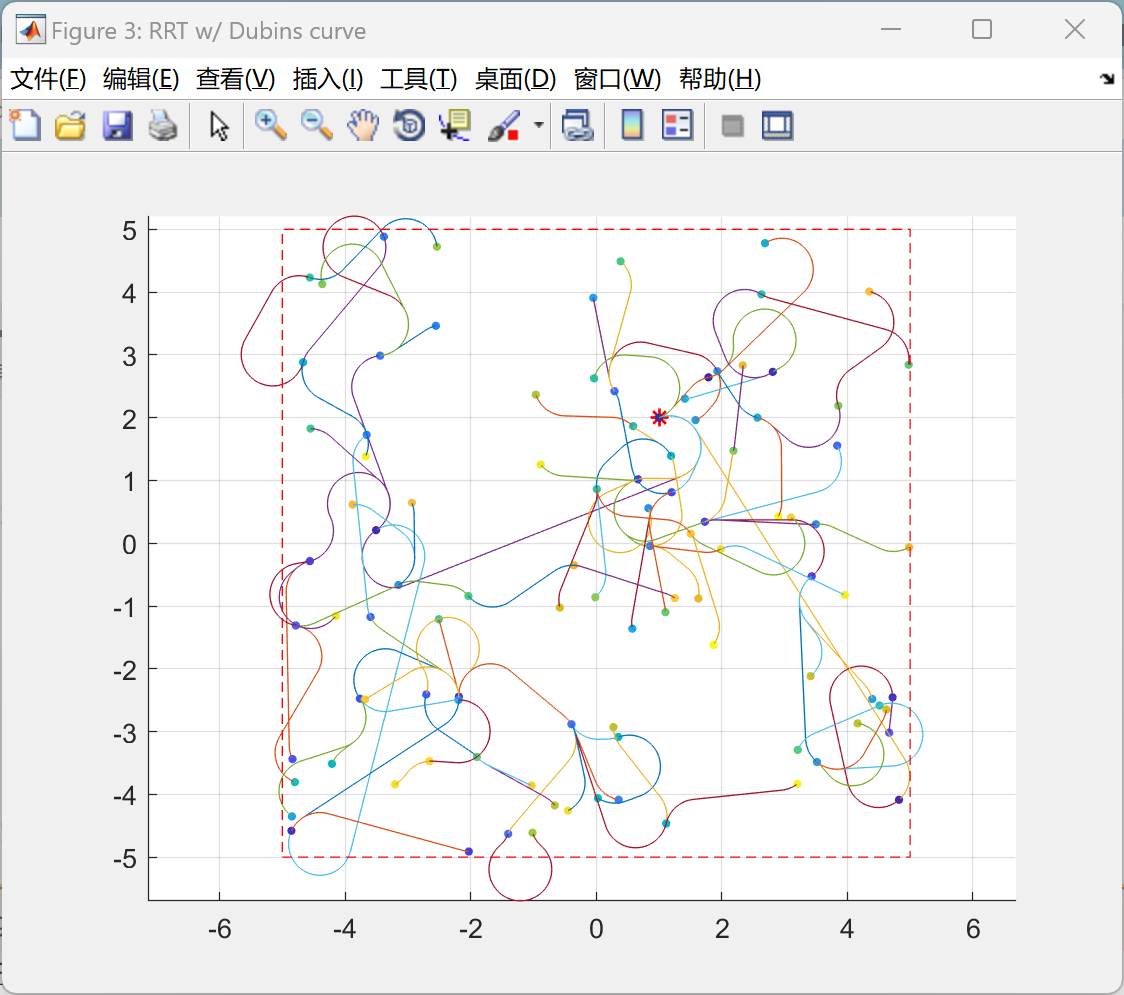
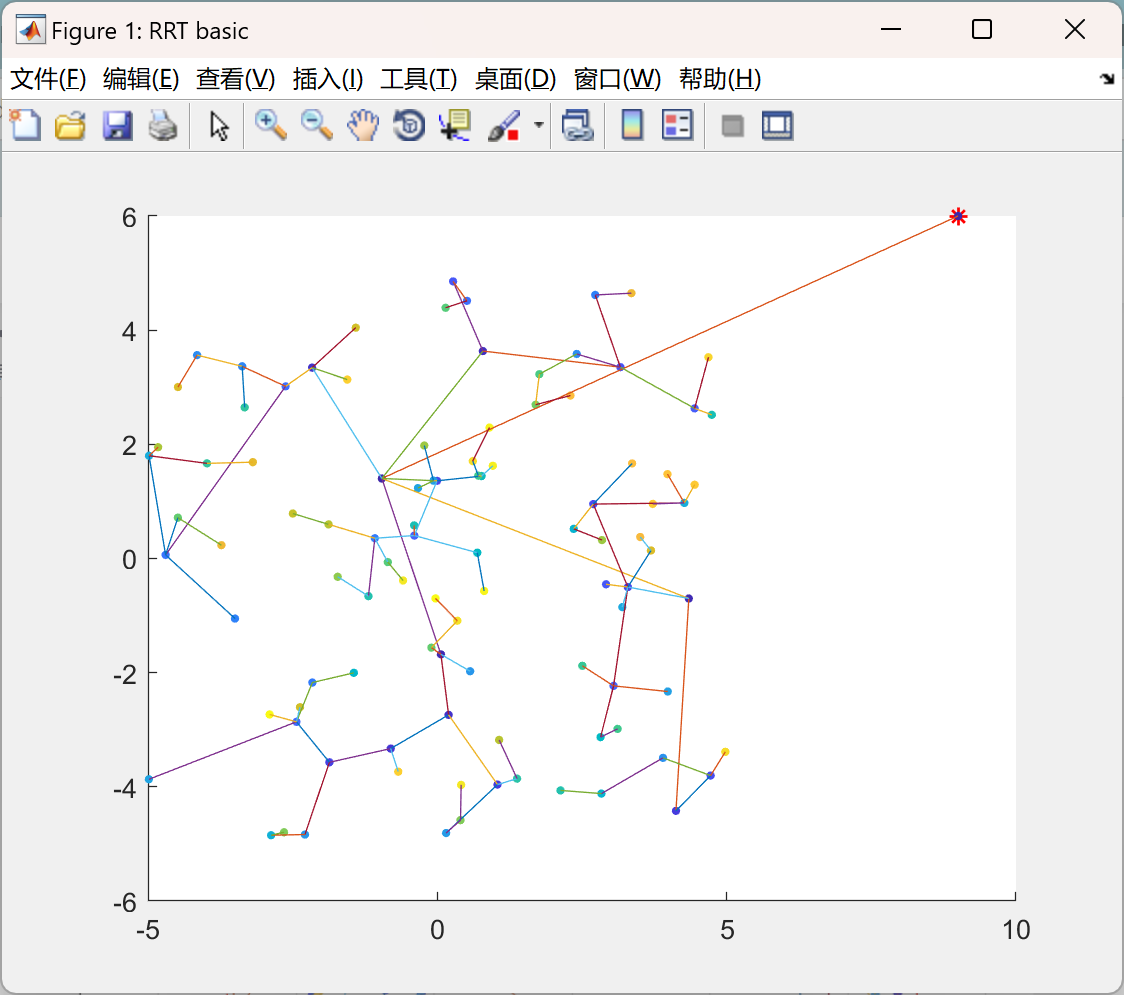
主函数部分代码：

close(findobj('type','figure','name','RRT basic'));
close(findobj('type','figure','name','RRT growing'));

%%%%%%%%%%%%%%%%%%%% User Configuration Area %%%%%%%%%%%%%%%%%%%%
% define the map
height = 20;
width = 20;
center = [0, 0];

% starting vertex
origin = [1,0];
iterations = 1000;

% define the obstacles using polygones, should be a cell stack of arrays.
poly = { [-4,-4; -1.5, -4; 0, -2.5; -0.5, -1; -3, 0],...
         [0,3; 3,3; 3, 6; 4, 6; 1.5, 8; -1, 6; 0, 6] };
%%%%%%%%%%%%%%%%%%%% End of configuration area %%%%%%%%%%%%%%%%%%%%
     
offset = center - [width, height]./2;
vertecies = origin;
vert_count = 1;
edges.x = zeros(iterations,2);
edges.y = zeros(iterations,2);
ind_nearest = zeros(iterations,1);
edge_count = 0;

% figure('name', 'RRT growing'); % originally for real-time animation
tic;
for i=1:iterations
    % random point generation
    x_rand = width*rand() + offset(1);
    y_rand = height*rand() + offset(2);
    
    % connect to nearest point
    ind_nearest(i) = dsearchn(vertecies, [x_rand, y_rand]);
    edge_rand = [x_rand, y_rand ; vertecies(ind_nearest(i),:)];
    
    % check availablility
    if chk_collision(edge_rand,poly) == 0
        
        % connect and add to list
        vertecies(vert_count+1,:) = [x_rand, y_rand];
        vert_count = vert_count + 1;
        edges.x(edge_count+1,:) = [vertecies(ind_nearest(i),1), x_rand];
        edges.y(edge_count+1,:) = [vertecies(ind_nearest(i),2), y_rand];
        edge_count = edge_count + 1;
    else
        %i = i - 1;         % doesn't work under MATLAB
    end
    
    % plot animation here is undoable probably due to MATLAB running
    % optimization...
    % scatter(x_rand, y_rand, 10,'filled'); hold on;
    % plot([vertecies(ind_nearest(i),1); x_rand], [vertecies(ind_nearest(i),2); y_rand]); hold on;
end
toc;
clear i x_rand y_rand edge_rand

figure('name', 'RRT basic');
scatter(origin(1), origin(2), 45, '*','r','LineWidth',1); hold on;
scatter(vertecies(:,1), vertecies(:,2), 10,linspace(1,10,length(vertecies(:,1))),'filled'); hold on;
plot(edges.x', edges.y'); hold on;