【状态估计】用于磁针状态估计的 EKF 和 UKF 模型（Matlab实现）

原创已于 2024-11-24 19:44:20 修改 · 393 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

于 2024-11-24 19:41:42 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

用于磁针状态估计的 EKF 和 UKF 模型概述扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波器（UKF）模型被应用于磁针状态估计领域。 EKF 是一种著名的滤波方法，它围绕当前估计状态对非线性系统进行线性化。在磁针状态估计的背景下，EKF 试图通过结合基于系统模型的预测步骤和纳入新测量值的更新步骤来估计磁针的状态。然而，EKF 中的线性化过程可能会引入误差和不准确性，特别是当系统的非线性程度显著时。另一方面，UKF 被设计用于处理非线性系统而无需进行线性化。它使用一组精心选择的采样点（称为西格玛点）来捕获状态分布的均值和协方差。这些西格玛点通过非线性系统模型传播，然后用于估计更新后的状态和协方差。在磁针状态估计的情况下，与 EKF 相比，UKF 可能提供更准确的状态估计，特别是当磁针的行为高度非线性时。这两种模型都有各自的优点和局限性。在 EKF 和 UKF 之间进行选择取决于诸如磁针系统的复杂性、非线性程度、可用的计算资源以及状态估计的准确性要求等因素。

📚2 运行结果

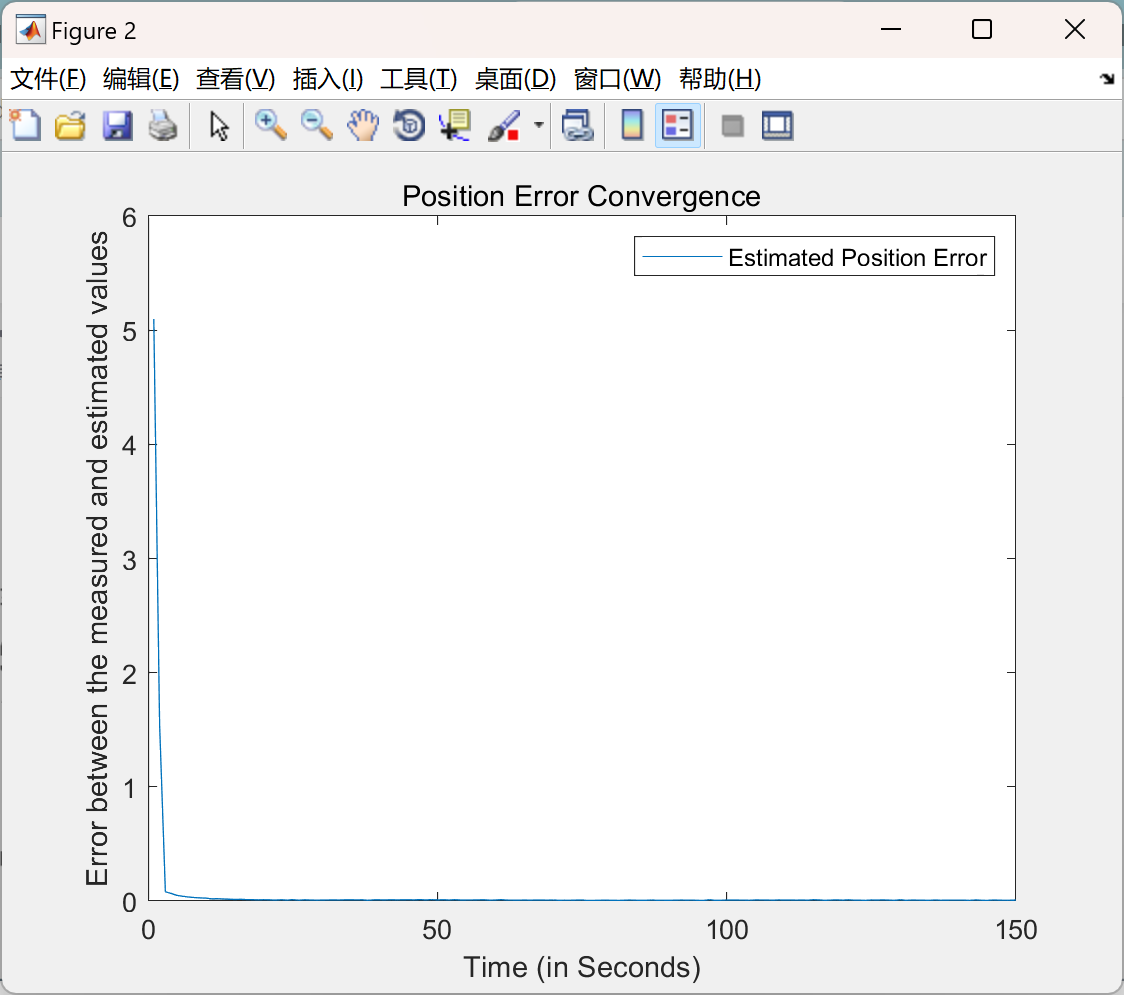
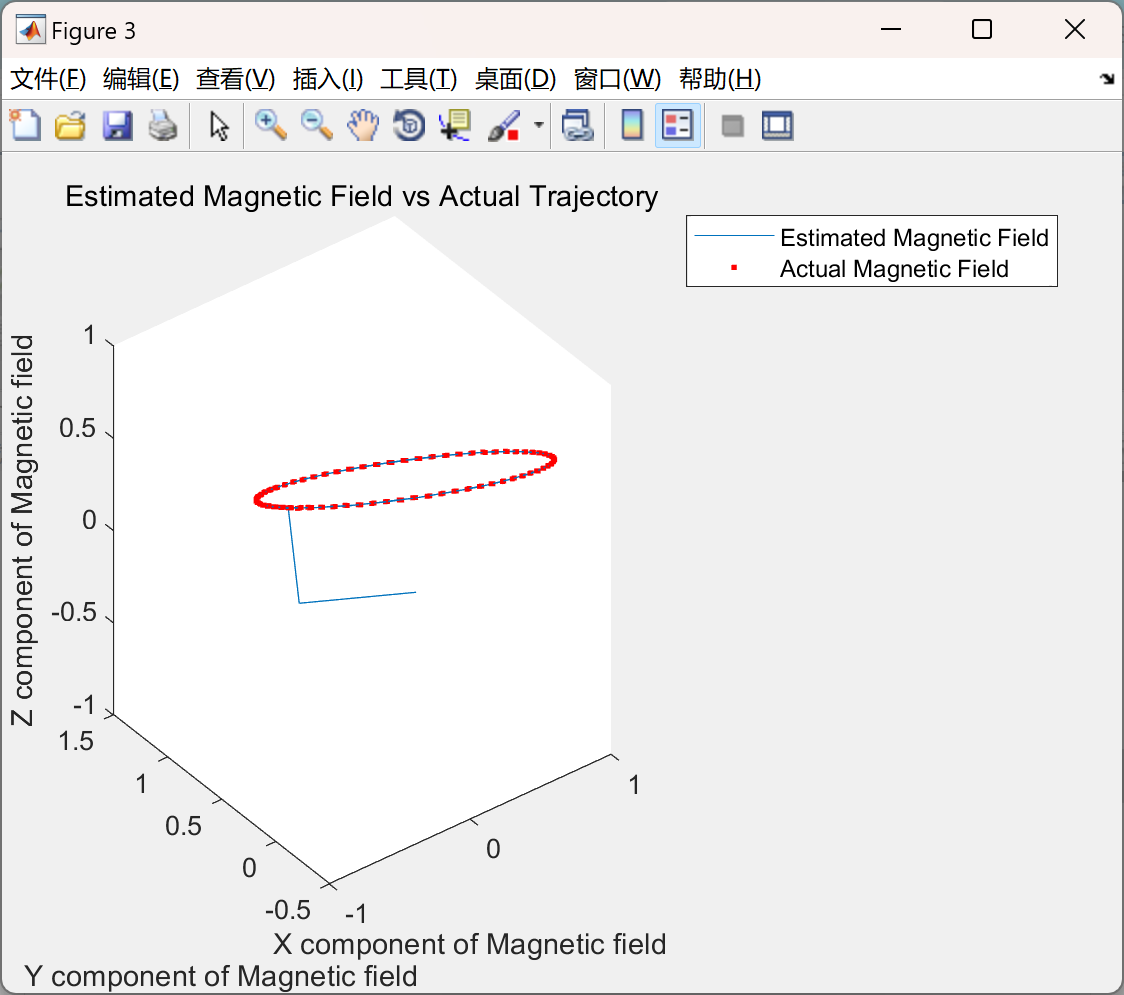
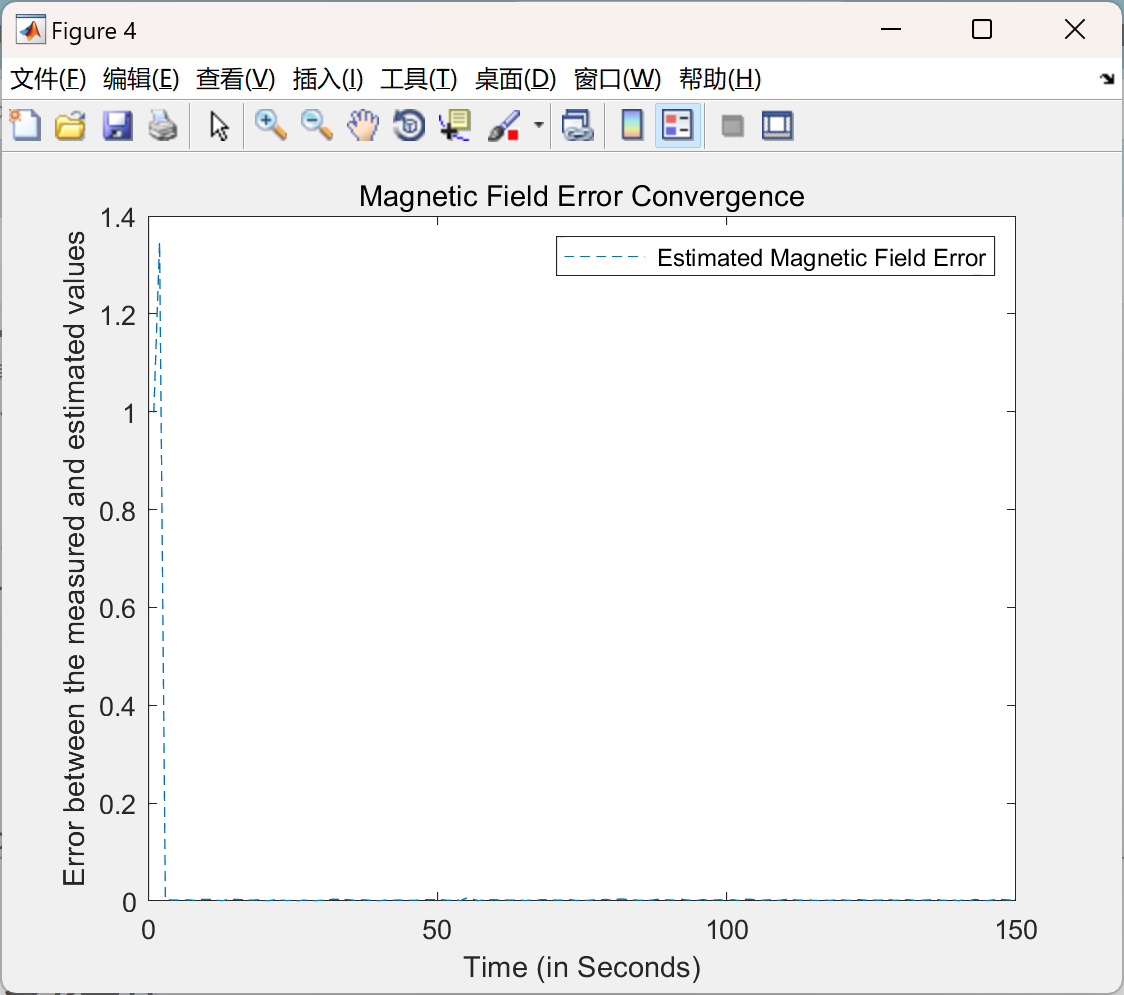
主函数部分代码：

%% System Inputs initialization
v=3;
omega=[1;2;3];
%% Parameters Initialization
numt = 150; % time steps of the trajectory
tspan=[0 0.025]; % time period of integration
d=9; % Dimensionality of the state vector
muBar_state=zeros(9,1,numt); % Mean state Vector
real_obv=zeros(6,numt); % Measurements from the real system
state_trajec=zeros(9,numt); % State Measurements from the real system
observation=zeros(6,1,2*d+1,numt); % Observation vectors for each sigma point
sv_sp=zeros(9,1,2*d+1); % State vectors for each sigma point
sp=zeros(9,1,2*d+1); % Sigma Points
sp_tr=zeros(9,1,2*d+1); % Sigma Points after the first transformation
muBar_obv=zeros(6,1,numt); % Mean observation vector
InoCov=zeros(6,6); % Innovation Covariance Martrix
SO_Cov=zeros(9,6); % State-Observation Covariance matrix
mu_t=zeros(9,numt); % Mean State vector matrix
a= zeros(9,1,1,1); % Buffer variable for Mean of State vector Sigma Points
b= zeros(9,9);     % Buffer variable for Covariance of the transformed Sigma Points
q= zeros(6,1,1,1); % Buffer variable for Mean Observation
L=zeros(6,6,1,1);  % Buffer variable for Innovation covarianc
x1=zeros(9,6);     % Buffer variable for State-Observation Covariance
R=0.01*eye(9); % Noise covariance of process
Q=diag([.001,.001,.001,.001,.001,.001]); % Noise covariance of observation (measurement)
mu_treal=[1;3;4;0;1;0;0;1;0]; % Actual initial state vector

%%  trajectory Generator
for trajec=1:numt %%iteration for each sigma point
    if (trajec==1)
        state_trajec(1:9,trajec)=mu_treal(:,1); %%state vector at time =1
        
    else
        
        [jk,ele]=ode45(@(trajec,x)statevecInteg(trajec,x,v,omega),tspan,state_trajec(1:9,trajec-1));
        state_trajec(1:9,trajec)=ele(end,:)';
        
    end
    
    real_obv(:,trajec)=observe(state_trajec(1:3,trajec),state_trajec(7:9,trajec)) + Q*randn(6,1);
end
%% weights and Covariance Initialization
[wt_pt,wt_cov]=sigmaPntCovWt(d);
covariance(1:9,1:9)= eye(9);
mu_t(1:9,1) = state_trajec(1:9,1)+randn(9,1);
%% Filter
for t=2:numt %% iterations for time steps equal to 0.025 seconds
    %% Sigma Points for each state vector
    sp(1:9,1,1:2*d+1)=sigmapnt(mu_t(1:9,t-1),covariance(1:9,1:9),d);
    
    %% Vector rates integration
    
    for sgmp=1:2*d+1 %%iteration for each sigma point
        [xy,element]=ode45(@(t,x)statevecInteg(t,x,v,omega),tspan,sp(1:9,1,sgmp));
        sv_sp(1:9,1,sgmp)=element(end,:)';
    end
    
    %% Mean of State vector Sigma Points
    a = zeros(9,1,1,1);
    for msgmp=1:2*d+1
        a = a+wt_pt(msgmp)*sv_sp(1:9,1,msgmp);
    end
    muBar_state(:,1,t) = a;
    
    %% Covariance of the transformed Sigma Points
    b= zeros(9,9);
    for msgmcov=1:2*d+1
        covariance(1:9,1:9)= b+wt_cov(msgmcov)*(sv_sp(1:9,1,msgmcov)-muBar_state(1:9,1,t))*(sv_sp(1:9,1,msgmcov)-muBar_state(1:9,1,t))';
        b=covariance(1:9,1:9);
    end
    covariance(:,:)=covariance(:,:)+R;
    %% Sigma points around the transformed mean
    
    sp_tr(1:9,1,1:2*d+1)=sigmapnt(muBar_state(1:9,1,t),covariance(1:9,1:9),d);