【无迹卡尔曼滤波】不确定和间接测量的非线性动力系统识别研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及文章

---

💥1 概述

文献来源：

摘要
本文回顾了从连续非线性动力系统的嘈杂时间序列测量中估计参数和未观测轨迹组成部分的问题。首先指出，在不明确考虑测量误差的参数估计技术（如回归方法）中，嘈杂的测量可能导致不准确的参数估计。另一个问题是，对于混沌系统，必须最小化的成本函数如此复杂，以至于常见的优化程序可能会失败。我们表明，包含关于基础轨迹的时间连续性的信息可以显著改善参数估计。本文详细描述了两种方法，这两种方法都考虑了变量误差问题和复杂成本函数的问题：分射法和递归估计技术。这两种方法都在数值示例上进行了演示。

关键词：系统识别 多重分射算法 无迹卡尔曼滤波 最大似然

📚2 运行结果

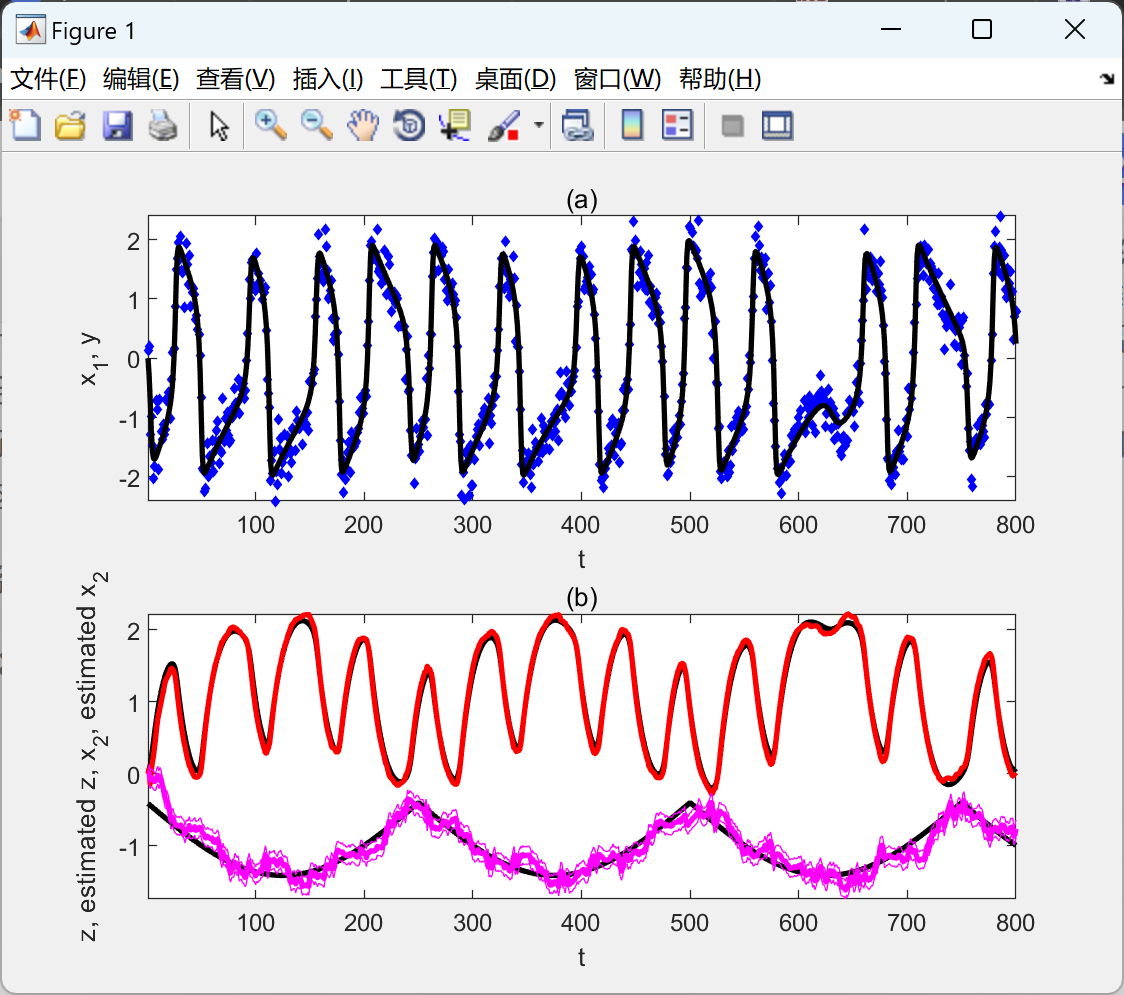
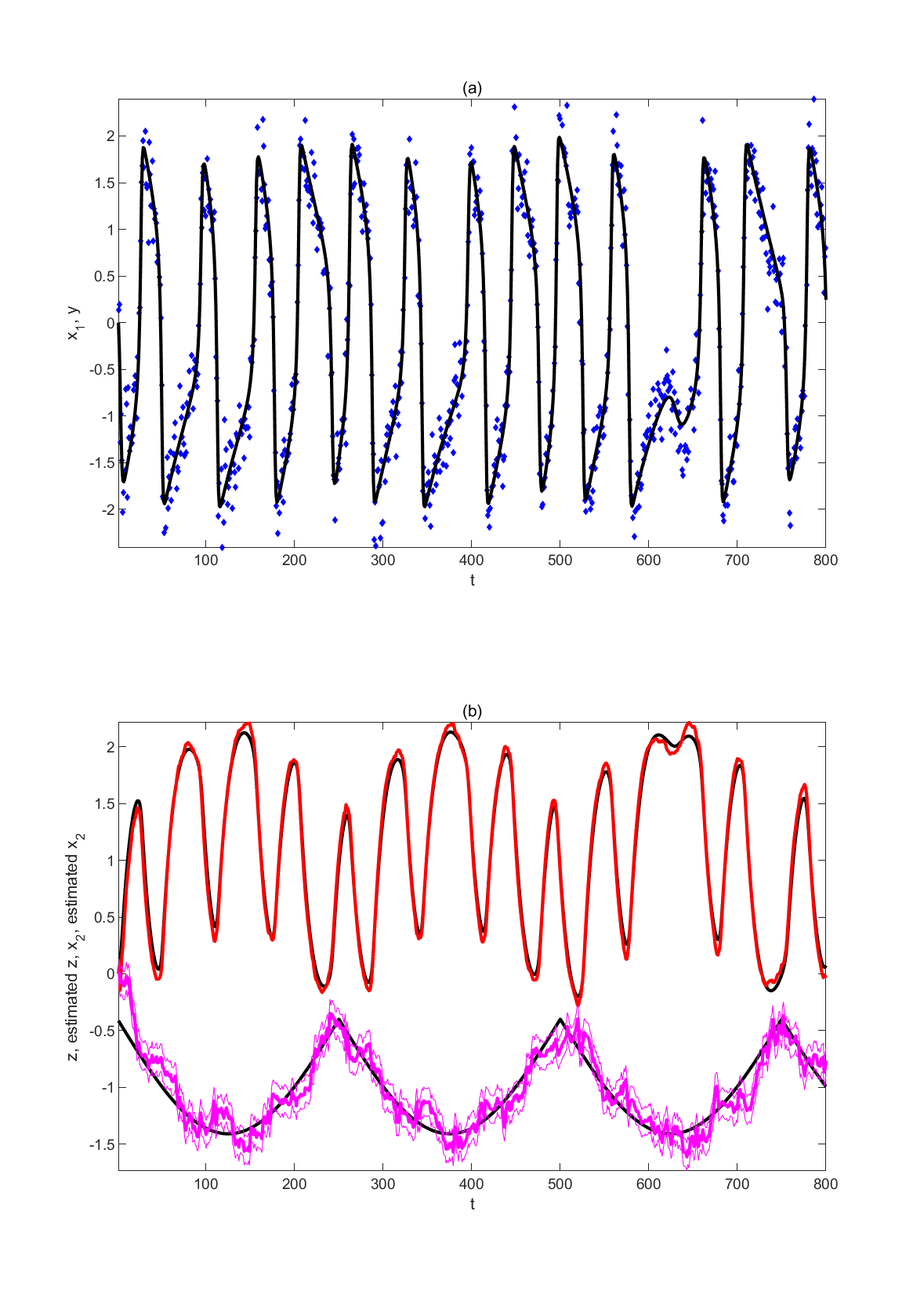
部分代码：

% Results %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

chisq=mean((x(1,:)-xhat(1,:)).^2+(x(2,:)-xhat(2,:)).^2+(x(3,:)-xhat(3,:)).^2);
disp(['Chi square = ',num2str(chisq)]);

% Showing last estimated parameter, used for example for the final estimate of a constant parameter:
% est=xhat(1:dq,ll)'; disp(['Estimated x = ' num2str(est)]);
% error=errors(1:dq,ll)'; disp(['Error = ' num2str(error)]);

figure(1)

subplot(2,1,1)
plot(y,'bd','MarkerEdgeColor','blue', 'MarkerFaceColor','blue','MarkerSize',3);
hold on;
plot(x(dq+1,:),'black','LineWidth',2);
%plot(xhat(dq+1,:),'r','LineWidth',2);
xlabel(texlabel('t'));
ylabel(texlabel('x_1, y'));
hold off;
axis tight
title('(a)')
drawnow

subplot(2,1,2)
plot(x(dq+2,:),'black','LineWidth',2);
hold on
plot(xhat(dq+2,:),'r','LineWidth',2);
plot(x(1,:),'black','LineWidth',2);
for i=1:dq; plot(xhat(i,:),'m','LineWidth',2); end
for i=1:dq; plot(xhat(i,:)+errors(i,:),'m'); end
for i=1:dq; plot(xhat(i,:)-errors(i,:),'m'); end
xlabel(texlabel('t'));
ylabel(texlabel('z, estimated z, x_2, estimated x_2'));
hold off
axis tight
title('(b)')

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码及文章